时间复杂度与空间复杂度的理解与计算

Posted 2021-03-24 cupe

小白的我总是搞不清楚

因此做个整理（来源http://data.biancheng.net/view/2.html）

算法是解决某个问题的想法、思路；而程序是在心中有算法的前提下编写出来的可以运行的代码。

• 算法的运行时间。（称为“时间复杂度”）
• 运行算法所需的内存空间大小。（称为“空间复杂度”）

 

时间复杂度

由于是估算算法的时间复杂度，相比而言，循环结构对算法的执行时间影响更大。

所以，算法的时间复杂度，主要看算法中使用到的循环结构中代码循环的次数（称为“频度”）。次数越少，算法的时间复杂度越低。

a) ++x; s=0;
b) for (int i=1; i<=n; i++) { ++x; s+=x; }
c) for (int i=1; i<=n; i++) { for (int j=1; i<=n; j++) { ++x; s+=x; } }

上边这个例子中，a 代码的运行了 1 次，b 代码的运行了 n 次，c 代码运行了 n*n 次。

算法的时间复杂度的表示方式为：

O(频度)

这种表示方式称为大“O”记法。

 

对于上边的例子而言，a 的时间复杂度为O(1)，b 的时间复杂度为O(n)，c 的时间复杂度为为O(n2)。

如果a、b、c组成一段程序，那么算法的时间复杂度为O(n2+n+1)。但这么表示是不对的，还需要对n2+n+1进行简化。

简化的过程总结为3步：

• 去掉运行时间中的所有加法常数。（例如 n²+n+1，直接变为 n²+n）
• 只保留最高项。（n²+n 变成 n²）
• 如果最高项存在但是系数不是1，去掉系数。（n² 系数为 1）

所以，最终a、b和c合并而成的代码的时间复杂度为O(n2)。

 

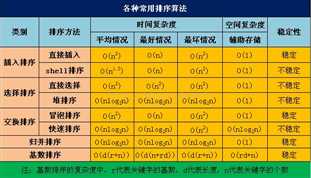
几种常见的算法时间复杂度的比较（又小到大）：

O(1)常数阶 < O(logn)对数阶 < O(n)线性阶 < O(n2)平方阶 < O(n3)(立方阶) < O(2n) (指数阶)

 

空间复杂度

算法的时间复杂度和空间复杂度是可以相互转化的。

【

如果算法执行所需要的临时空间不随着某个变量n的大小而变化，即此算法空间复杂度为一个常量，可表示为 O(1)

int i=1;

int j=2;

++i;

j++;

int m=i+j;

代码中的 i、j、m 所分配的空间都不随着处理数据量变化，因此它的空间复杂度 S(n) = O(1)。

 

int[] m = new int[n]
for(i=1; i<=n; ++i)
{
   j = i;
   j++;
}
这段代码中，第一行new了一个数组出来，这个数据占用的大小为n，这段代码的2-6行，虽然有循环，但没有再分配新的空间，因此，这段代码的空间复杂度主要看第一行即可，即 S(n) = O(n)
原文链接：https://blog.csdn.net/jsjwk/article/details/84315770

】
谷歌浏览器相比于其他的浏览器，运行速度要快。是因为它占用了更多的内存空间，以空间换取了时间。
算法中，例如判断某个年份是否为闰年时，如果想以时间换取空间，算法思路就是：当给定一个年份时，

判断该年份是否能被4或者400整除，如果可以，就是闰年。

如果想以空间换时间的话，判断闰年的思路就是：把所有的年份先判断出来，存储在数组中（年份和数组下标对应），

如果是闰年，数组值是1，否则是0；当需要判断某年是否为闰年时，直接看对应的数组值是1还是0，不用计算就可以马上知道。

 

 

 

（下面这个图片一定，要，理解并记住啊。。。下次整理代码实现= =）