图论篇4——拓扑排序

Posted 2021-03-24 czc1999

引入

AOV网络

　　在有向图中，用顶点表示活动，用有向边<V_i, V_j>表示活动 i 是活动 j 的必须条件。这种有向图称为用顶点表示活动的网络(Active on vertices)，简称AOV网络。 
在AOV网络中，如果活动V_i必须在V_j之前进行，则存在有向边<V_i, V_j>，并称V_i是V_j的直接前驱，V_j是V_i的直接后继。这种前驱与后继的关系具有传递性和反自反性，这要求AOV网络中不能出现回路，即有向环。因此，对于给定的AOV网络，必须先判断它是否存在有向环。

拓扑排序

　　检测有向环可以通过对AOV网络进行拓扑排序，该过程将各个顶点排列成一个线性有序的序列，使得AOV网络中所有的前驱和后继关系都能得到满足。 如果拓扑排序能够将AOV网络的所有顶点都排入一个拓扑有序的序列中，则说明该AOV网络中没有有向环，否则AOV网络中必然存在有向环。AOV网络的顶点的拓扑有序序列不唯一。可以将拓扑排序看做是将图中的所有节点在一条水平线上的展开，图的所有边都从左指向右。

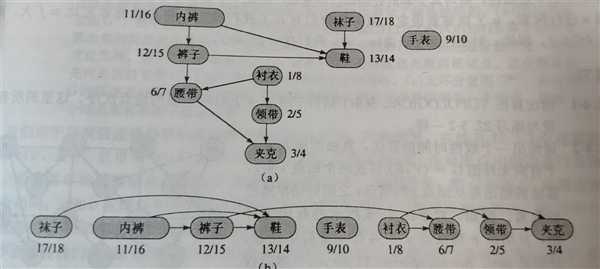
　　用穿衣服的次序来描述拓扑排序，图(a)表示必须先穿某些衣服，才可以穿其他衣服，图(b)表示将拓扑排序后的有向无环图在一条水平线上展示出来。袜子和内裤属于同等级，在排序结果中谁先谁后无所谓。

算法描述

对于一个有向无环图

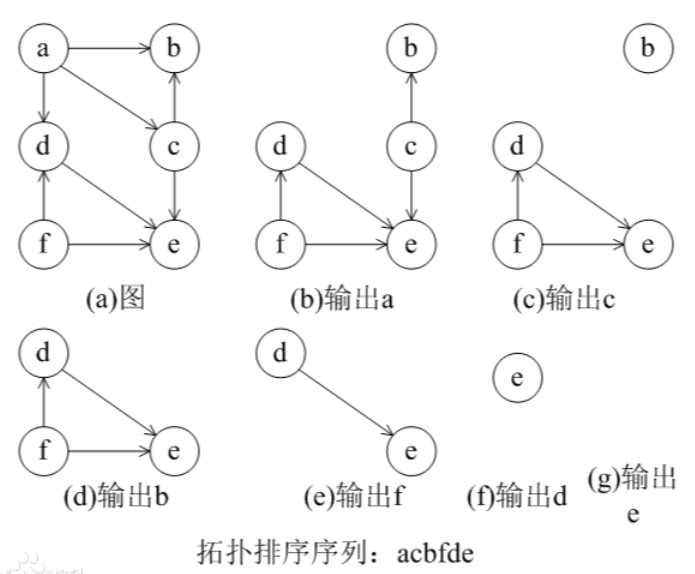
（1）统计所有节点的入度，对于入度为0的节点就可以分离出来，然后把这个节点指向所有的节点的入度$-1$。

（2）重复（1），直到所有的节点都被分离出来，拓扑排序结束。

（3）如果最后不存在入度为0的节点，那就说明有环，无解。

解释一下，假设A为一个入度为0的结点，就表示A结点没有前驱结点，可以直接做，把A完成后，对于A的所有后继结点来说，前驱结点就完成了一个，入度进行$-1$。

时间复杂度

　　如果AOV网络有n个顶点，e条边，在拓扑排序的过程中，搜索入度为零的顶点所需的时间是O(n)。在正常情况下，每个顶点进一次栈，出一次栈，所需时间O(n)。每个顶点入度减1的运算共执行了e次。所以总的时间复杂为O(n+e)。

因为拓扑排序的结果不唯一，所以题目一般会要求按某种顺序输出，就需要使用优先级队列，这里采取了最小字典序输出。

vector<int>head[505], ans;
int n, m, in[505];//入度序列

void topologicalSorting() {
        cin >> n >> m;
    for (int i = 0; i < m; i++) {
        int c1, c2;
        scanf("%d%d", &c1, &c2);
        head[c1].push_back(c2);
        in[c2]++;
    }
    priority_queue<int, vector<int>, greater<int>>q;
    for (int i = 1; i <= n; i++) {
        if (!in[i]) {
            q.push(i);
        }
    }
    while (!q.empty() && ans.size() < n) {
        int v = q.top(); q.pop();
        ans.push_back(v);
        for (int i = 0; i < head[v].size(); i++) {
            in[head[v][i]]--;
            if (!in[head[v][i]])
                q.push(head[v][i]);
        }
    }

    if (ans.size() == n) {
        //找到拓扑排序序列
    }
    else {
        //图中有环
    }
}    

练习

模板题

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1285

#include <iostream>
#include <algorithm>
#include <queue>
#include <stdio.h>
#include <vector>
using namespace std;

vector<int>head[505];
int in[505];

int main() {
    int n, m;
    while (cin >> n >> m) {
        priority_queue<int, vector<int>, greater<int>>q;
        vector<int>ans;
        for (int i = 0; i < m; i++) {
            int c1, c2;
            scanf("%d%d", &c1, &c2);
            head[c1].push_back(c2);
            in[c2]++;
        }
        for (int i = 1; i <= n; i++) {
            if (!in[i]) {
                q.push(i);
            }
        }

        while (!q.empty()) {
            int temp = q.top(); q.pop();
            ans.push_back(temp);
            for (int i = 0; i < head[temp].size(); i++) {
                in[head[temp][i]]--;
                if (!in[head[temp][i]])
                    q.push(head[temp][i]);
            }
        }
        if (ans.size() == n) {
            for (int i = 0; i < n; i++) {
                head[i + 1].clear();
                cout << ans[i];
                if (i != n - 1)cout << ‘ ‘;
            }
            cout << endl;
        }
        q.emplace();
        ans.clear();
        
    }
    
    return 0;
}

View Code

反向拓扑排序

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=4857

　　题意：$n$个结点，给定$m$个拓扑关系$(a,b)$表示$a$必须排在$b$前面，在满足$m$个拓扑关系关系的同时，使得小的结点尽可能的排在前面。
乍一看好像直接拓扑排序就行，但是看一个例子：

$6 ightarrow  3 ightarrow 15 ightarrow 4 ightarrow 2$

　　直接拓扑排序的结果是：$5 4 2 6 3 1$ ，是错误的，因为我们可以把1号安排到更前面的位置 即：$6 3 1 5 4 2$（正确答案）。所以直接拓扑排序是不行的，为什么会出现这样的状况，对于多个拓扑关系，我们本来的策略是优先删除首结点较小的拓扑序列（比如5号结点比6号结点小，我们先删除了5号结点），但我们希望的是优先删除尾结点较小的拓扑序列（比如1号结点比2号结点小，应当先删除1号结点）。问题找到了，我们可以尝试一下逆向思维，即我们先考虑哪些点应该靠后释放，就是把原来的拓扑关系反过来

$1 ightarrow 3 ightarrow 62 ightarrow 4 ightarrow 5$

这样我们按照优先删除首结点较大的拓扑序列得到的结果是$2 4 5 1 3 6$，好像还是不太对，把它逆序输出就对啦！

#include <iostream>
#include <algorithm>
#include <queue>
#include <stdio.h>
#include <vector>
using namespace std;

vector<int>head[30005];
int in[30005];

int main() {
    int T;
    cin >> T;
    while (T--) {
        int n, m;
        cin >> n >> m;
        priority_queue<int>q;
        vector<int>ans;
        for (int i = 0; i < m; i++) {
            int c1, c2;
            scanf("%d%d", &c1, &c2);
            /*head[c1].push_back(c2);
            in[c2]++;*/
            head[c2].push_back(c1);
            in[c1]++;
        }
        for (int i = 1; i <= n; i++) {
            if (!in[i]) {
                q.push(i);
            }
        }

        while (!q.empty()) {
            int temp = q.top(); q.pop();
            ans.push_back(temp);
            for (int i = 0; i < head[temp].size(); i++) {
                in[head[temp][i]]--;
                if (!in[head[temp][i]])
                    q.push(head[temp][i]);
            }
        }

        if (ans.size() == n) {
            for (int i = n - 1; i >= 0 ; i--) {
                head[i + 1].clear();
                cout << ans[i];
                if (i != 0)cout << ‘ ‘;
            }
            cout << endl;
        }
        q.emplace();
        ans.clear();
    }
    return 0;
}