基于线性回归分析——boston房价预测

Posted 2021-03-24 ohou

本文采用正规方程、梯度下降、带有正则化的岭回归三种方法对BOSTON房价数据集进行分析预测，比较三种方法之间的差异

from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression, SGDRegressor,  Ridge, LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error, classification_report
from sklearn.externals import joblib
import pandas as pd
import numpy as np

class HousePredict():
    """
    波士顿房子数据集价格预测
    """
    
    def __init__(self):
        
        # 1.获取数据
        lb = load_boston()

        # 2.分割数据集到训练集和测试集
        x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)
        # print(y_train, y_test)

        # 3.特征值和目标值是都必须进行标准化处理, 实例化两个标准化API
        # 3.1特征值标准化
        self.std_x = StandardScaler()

        self.x_train = self.std_x.fit_transform(x_train)
        self.x_test = self.std_x.transform(x_test)


        # 3.2目标值标准化
        self.std_y = StandardScaler()

        self.y_train = self.std_y.fit_transform(y_train.reshape(-1, 1))  # 二维
        self.y_test = self.std_y.transform(y_test.reshape(-1, 1))


    def mylinear(self):
        """
        正规方程求解方式预测
        :return: None
        """
        
        # 预测房价结果，直接载入之前保存的模型
    #     model = joblib.load("./tmp/test.pkl")

    #     y_predict = self.std_y.inverse_transform(model.predict(self.x_test))

    #     print("保存的模型预测的结果：", y_predict)

    #     estimator预测
    #     正规方程求解方式预测结果
        lr = LinearRegression() 
        lr.fit(self.x_train, self.y_train)

        print("正规方程求解方式回归系数", lr.coef_)

        # 保存训练好的模型
        # joblib.dump(lr, "./tmp/test.pkl")

        # # 预测测试集的房子价格
        y_lr_predict = self.std_y.inverse_transform(lr.predict(self.x_test))
        #
        # print("正规方程测试集里面每个房子的预测价格：", y_lr_predict)
        print("正规方程的均方误差：", mean_squared_error(self.std_y.inverse_transform(self.y_test), y_lr_predict))
        
        return None
    
    def mysdg(self):
        """
        梯度下降去进行房价预测
        :return: None
        """
        sgd = SGDRegressor()
        sgd.fit(self.x_train, self.y_train)

        print("梯度下降得出的回归系数", sgd.coef_)

        # 预测测试集的房子价格
        y_sgd_predict = self.std_y.inverse_transform(sgd.predict(self.x_test))

        # print("梯度下降测试集里面每个房子的预测价格：", y_sgd_predict)
        print("梯度下降的均方误差：", mean_squared_error(self.std_y.inverse_transform(self.y_test), y_sgd_predict))

        return None
    
    
    def myridge(self):
        """
        带有正则化的岭回归去进行房价预测
        """
        rd = Ridge(alpha=1.0)
        rd.fit(self.x_train, self.y_train)
        
        print("岭回归回归系数", rd.coef_)
        
        # 预测测试集的房子价格
        y_rd_predict = self.std_y.inverse_transform(rd.predict(self.x_test))
        
        # print("岭回归每个房子的预测价格：", y_rd_predict)
        print("岭回归均方误差：", mean_squared_error(self.std_y.inverse_transform(self.y_test), y_rd_predict))
        
        return None

if __name__ == "__main__":
    A = HousePredict()
    A.mylinear()
    A.mysdg()
    A.myridge()

正规方程求解方式回归系数 [[-0.10843933  0.13470414  0.00828142  0.08736748 -0.2274728   0.25791114
   0.0185931  -0.33169482  0.27340519 -0.22995446 -0.20995577  0.08854303
  -0.40967023]]

正规方程的均方误差： 20.334736834357248
梯度下降得出的回归系数 [-0.08498404  0.07094101 -0.03414044  0.11407245 -0.09152116  0.3256401
 -0.0071226  -0.2071317   0.07391015 -0.06095605 -0.17955743  0.08442426
 -0.35757617]

梯度下降的均方误差： 21.558873305580214
岭回归回归系数 [[-0.10727714  0.13281388  0.00561734  0.0878943  -0.22348981  0.25929669
   0.0174662  -0.32810805  0.26380776 -0.22163145 -0.20871114  0.08831287
  -0.4076144 ]]

岭回归均方误差： 20.37300555358197

过拟合：一个假设在训练数据上能够获得比其他假设更好的拟合， 但是在训练数据外的数据集上却不能很好地拟合数据，此时认为这个假设出现了过拟合的现象。(模型过于复杂)

• 原因：原始特征过多，存在一些嘈杂特征，模型过于复杂是因为模型尝试去兼顾各个测试数据点

• 解决办法：
  • 1.进行特征选择，消除关联性大的特征(很难做)
  • 2.交叉验证(让所有数据都有过训练)
  • 3.L2正则化
    • 作用：可以使得W的每个元素都很小，都接近于0（降权重，尽量减小高次项特征的影响）
    • 优点：越小的参数说明模型越简单，越简单的模型则越不容易产生过拟合现象

欠拟合：一个假设在训练数据上不能获得更好的拟合， 但是在训练数据外的数据集上也不能很好地拟合数据，此时认为这个假设出现了欠拟合的现象。(模型过于简单)

• 原因：学习到数据的特征过少
• 解决办法：增加数据的特征数量

1、LinearRegression与SGDRegressor评估

2、特点：线性回归器是最为简单、易用的回归模型。

从某种程度上限制了使用，尽管如此，在不知道特征之间关系的前提下，我们仍然使用线性回归器作为大多数系统的首要选择。

小规模数据：LinearRegression(不能解决拟合问题)以及其它

大规模数据：SGDRegressor

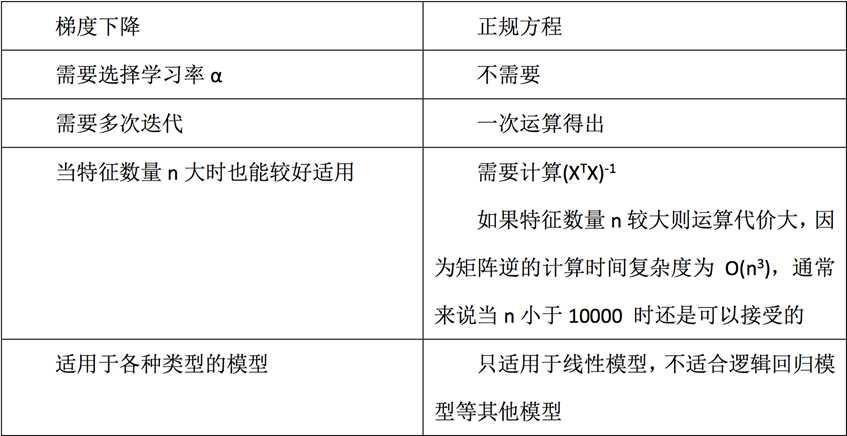
线性回归 LinearRegression与Ridge对比

岭回归：回归得到的回归系数更符合实际，更可靠。另外，能让估计参数的波动范围变小，变的更稳定。在存在病态数据偏多的研究中有较大的实用价值