POJ 2182 Lost Cows

Posted 2021-03-24 sahdsg

http://poj.org/problem?id=2182

题目

有一些编号从1到n的牛，排成了一行，但是没有按编号从小到大排，某人知道每个位置的左边有多少个编号比这个位置小，问每个位置的牛的编号是多少。$n<10^5$

题解

先考虑后面的牛，直接模拟，用剩下的排第a[i]+1的编号

但是直接模拟会超时，所以可以用数状数组维护前缀和，如果这个编号用了就设为0，没用就设为1，找第几个编号就可以二分前缀和

所以时间复杂度是$mathcal{O}(nlog n imeslog n)$

仔细观察树状数组的结构

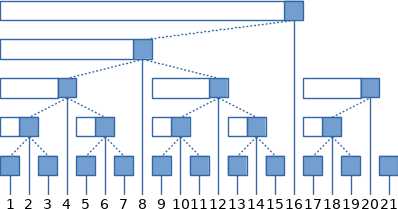
 可以发现找某个前缀和可以只是用从上往右下或者下走（不往左下走），那么类似于二分，

 

 如果当前的是大于等于z，就舍弃，如果<z就选用，那么最后一个<z的右边那个就是第一个=z的（因为每次最多+1）

从上往下走最多走$log(n)$步，时间复杂度是$mathcal{O}(nlog{n})$

AC代码（好神奇啊！）

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define REP(i,a,b) for(register int i=(a); i<(b); i++)
#define REPE(i,a,b) for(register int i=(a); i<=(b); i++)
#define PERE(i,a,b) for(register int i=(a); i>=(b); i--)
#ifdef sahdsg
#define DBG(...) printf(__VA_ARGS__)
#else
#define DBG(...) void(0)
#endif
#define MAXN 8007
int dt[MAXN];
int fw[MAXN];
int ans[MAXN];
int lg2[MAXN];
int n;
inline void db() {
	lg2[0]=0;
	REPE(i,1,n) {
		lg2[i]=((i&(i-1))==0)?lg2[i-1]+1:lg2[i-1];
	}
}
int ask(int x) {
	int ans=0;
	for(; x; x-=x&-x) ans+=fw[x];
	return ans;
}
void add(int x, int v) {
	for(; x<=n; x+=x&-x) fw[x]+=v;
}
int main() {
	scanf("%d", &n); db();
	dt[0]=0;
	REP(i,1,n) {
		scanf("%d", &dt[i]);
	}
	REPE(i,0,n) {
		fw[i]=0;
	}
	REPE(i,1,n) {
		add(i,1);
	}
	PERE(i,n-1,0) {
		int z=dt[i]+1;
		int pos=0, sum=0, st=1<<lg2[n];
		while(st>0) {
			if(pos+st<=n && sum+fw[pos+st]<z) {
				sum+=fw[pos+st];
				pos+=st;
			}
			st>>=1;
		}
		add(pos+1,-1);
		ans[i]=pos+1;
	}
	REP(i,0,n) {
		printf("%d
", ans[i]);
	}
	return 0;
}