算法概论
Posted zhai1997
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了算法概论相关的知识,希望对你有一定的参考价值。
1、算法与数据结构的关系:
(1)数据结构+算法=程序
数据结构是对数据的描述,算法是对数据的操作,因此:数据结构+算法=程序
算法侧重于对解决问题的方法的描述。
程序是对一个算法的具体实现。
(2)联系:
数据结构是算法设计的基础。
算法的操作对象是数据结构。
数据结构设计主要是选择数据的存储方式,算法设计是在选择的数据结构基础上设计一个好的算法。
数据结构关注的是数据的逻辑结构、存储结构、基本操作,而算法关注的是如何在数据结构基础上解决实际问题。
2、算法设计的目标:
(1)正确性:正确地执行预先规定的功能和性能要求。
(2)可使用性(用户友好性):可以很方便地使用。
(3)可读性:易于理解。
(4)健壮性:提供异常处理,能够对不合理的数据进行检查。
(5)高效率与低存储:执行时间短的算法效率高,所需的最大存储容量低的算法好。
3、算法的重要特性:
(1)有限性:执行有限步之后结束。
(2)确定性:每一条指令无二义性。
(3)可行性:每一条运算都能精确地执行。
(4)输入性:一个算法有零个或多个输入。
(5)输出性:一个算法有一个或多个输入。
4、算法分析:
(1)时间复杂度分析:
问题规模:算法的执行时间主要与问题规模有关,它是算法执行输入量的多少,是问题大小的本质表示。如:数组的元素个数、矩阵的阶数。
基本语句:算法的基本语句是执行次数与整个算法的执行次数成正比的语句,他对算法的执行时间贡献最大(最深层循环内的语句)。

(2)渐进符号
大O符号:f(n)=O(g(n)),f(n)是g(n)的大O,当且仅当存在正常量c和n0,使得当n>=n0时,f(n)<=c(g(n)),即g(n)是f(n)的上界。
大Ω符号:f(n)=Ω(g(n)),f(n)是g(n)的大Ω,当且仅当存在正常量c和n0,使得当n>=n0时,f(n)>=c(g(n)),即g(n)是f(n)的下界
大θ符号:f(n)=θ(g(n)),f(n)是g(n)的大θ,当且仅当存在正常量c1,c2和n0,使得当n>=n0时,c1(g(n))<=f(n)<=c2(g(n)),,即g(n)与f(n)同阶
(3)递归算法的时间复杂度分析:
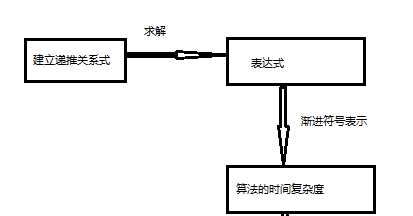
规模减小一倍的情况:
void mergesort(int a[],int i,int j){ int m ; if(i!=j) { m=(j+i)/2; mergesort(a,i,m);//归并排序 mergesort(a,m+1,j); merge(a,i,j,m);//两个有序子序列的合并,非递归函数,时间复杂度为O(n) } }

规模减一的情况:
#include<stdio.h> void hanoi(int n,char A,char B,char C){//n代表 a柱子上面的盘子数量 if(n==1){ printf("%c->%c ",A,C);//如果只有一个盘子,直接从 A 移动到 C }else{ hanoi(n-1,A,C,B);//将 n-1个盘子从 A 移动到 B printf("%c->%c ",A,C); hanoi(n-1,B,A,C); //将 n-1个盘子从 B 移动到 C } } main(){ hanoi(3,‘A‘,‘B‘,‘C‘) ; }

4、递归算法的空间复杂度分析
在对算法的存储空间进行分析的时候,只考虑临时变量所占的空间(形参所占用的空间不计入在内,形参所占用的空间会在调用该算法的算法中去考虑),空间复杂度是对一个算法在运行过程中临时占用的存储空间的度量,也是问题规模n的函数。
int maxelen( int a[],int i,intj){ int mid=(i+j)/2,maxl,max2; //临时变量 if(i<j) { max1=maxelem(a,i,mid); max2=maxelem(a,mid+1,j); return(max1>max2)?max1:max2; } else return a[i]; }
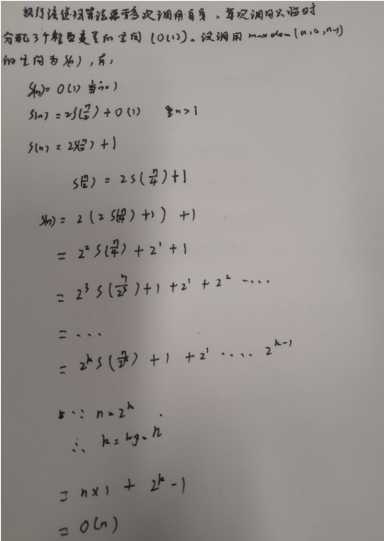
以上是关于算法概论的主要内容,如果未能解决你的问题,请参考以下文章