算法练习题力扣练习题——数组： 在有序数组中查找元素存在的范围

Posted 2021-03-22 ricardoislearning

原题说明：给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。

你的算法时间复杂度必须是 O(log n) 级别。

如果数组中不存在目标值，返回 [-1, -1]。

原题链接：https://leetcode-cn.com/problems/find-first-and-last-position-of-element-in-sorted-array

---

 

题目分析：

这道题目当然也是用二分查找来解题。经过上道题的教训，这次我详细考察了各个实例的可能（特别是空集以及数组元素比较少的时候可能出现的各种情况）。

那么整体上，这道题我当时觉得要写两个查找算法的函数，

PART1：第一个用于“随便”确定一个索引位置，其数值只要是目标值即可。

PART2：以索引值分别作为左半区间和右半区间的右边界和左边界，两边各自做一个二分查找。起初觉着第二部分用一个函数就行，后来在代入左半区间查找的时候发现，应该拆成两个函数会更方便一些。

 

下面是具体分析——

PART1：找到索引值

先po源代码

 1 private int[] locate(int[] nums, int left, int right, int target) {
 2     int mid = (left+right+1)>>1;
 3     int val = -1;
 4     while(left<=right) {
 5         if(nums[mid]==target) {
 6             val = mid;
 7             break;
 8         }
 9         else if(nums[mid]<target) {
10             left=mid+1;
11             mid=(left+right+1)>>1;
12         }
13         else if(nums[mid]>target) {
14             right=mid-1;
15             mid=(left+right+1)>>1;
16         }            
17     }
18     //val=(nums[left]==target)?left:val;
19     int[] borders = {left,right,val};
20     return borders;
21 }

 有上一篇的博客分析铺垫，二分查找的细节这里就不多提。需要说明的是我这里最后输出的变量形式，为什么要一起输出二分查找最后的左边界和右边界呢？这里给出一个实例${0,1,1,1,2,3,4,5,5,5}$，那么当$target$是$1$的时候，最后这部分查找完，左边界索引应该是$0$，右边界索引是$4$，查找到的索引值是$2$，那么之后的查找范围就迅速缩小了。

 

PART2：

分析左边区间的查找，代码如下

 1 private int left_binary_search(int[] nums, int left, int right, int target) {
 2     int mid = (left+right+1)>>1;
 3     int val = right;
 4     
 5     while(left<=right) {
 6         if(nums[mid]<target) {
 7             left=mid+1;
 8             mid=(left+right+1)>>1;
 9         }
10         else {
11             if(mid>0&&nums[mid-1]==target) {
12                 right=mid-1;
13                 mid=(left+right+1)>>1;
14             }
15             else if(mid>0&&nums[mid-1]!=target) {
16                 val = mid;
17                 break;
18             }
19             else if(mid==0)
20                 return 0;
21         }
22     }
23     return val;
24 }

 首先，返回值$val$在这里是作为最后输出的左边界。那么我设定输出值的初值就是上一步查找得到的索引值，这样就包括了最后数组中只有一个目标值得情况，同时也是左边区间的右边界。

然后需要分成两种情况讨论（如图1）：

 

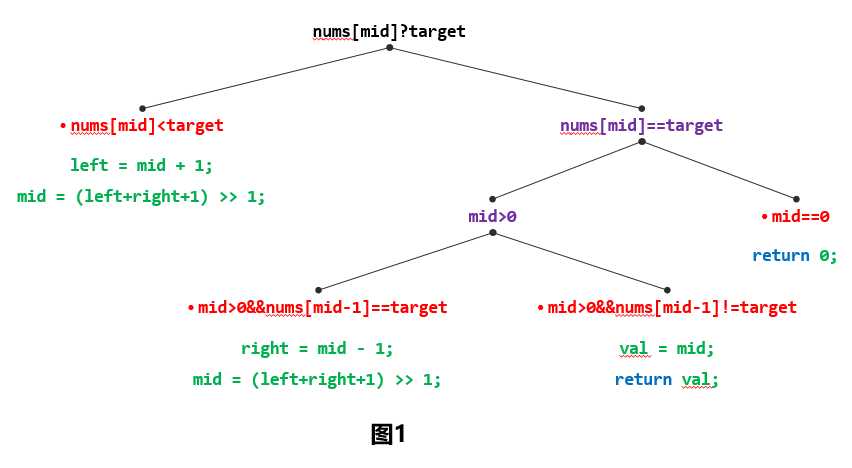
情况1，$nums[mid]<target$，那么这个时候目标值应该在搜索区间的右半边（默认递增数列）。此时应该移动左边界。

情况2，$nums[mid]==target$，即算法找到了左边区间内目标值的位置。但是这里要注意，标准的二分查找此时应该结束，然而题目要求需要找到所有重复的目标值的索引，所以需要让$mid$指针继续移动。怎么做呢？

可以看图2，由于是递增数列，那么在本情况下，$mid$到$right$之间应该都是目标值，若还要继续，则应该在$mid-1$的索引位置出现目标值，$right$取值$mid-1$；反之，则结束（因为重复数字必然构成连续）或继续查找直到满足循环的终止条件。

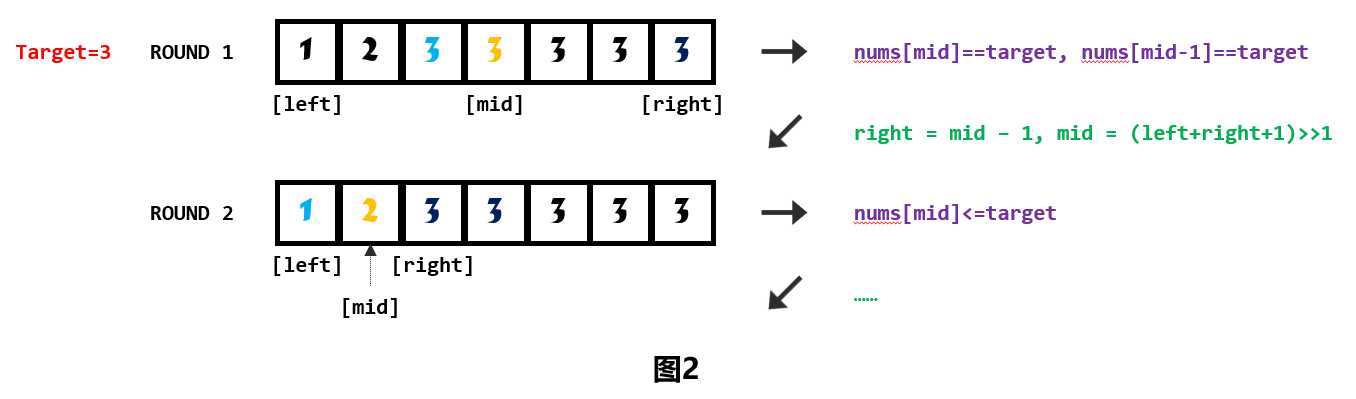
这里比较担心的情况是数组越界。所以对于左区间，在分支语句的判断条件上加入了$mid>0$，确保$mid-1$一定有值可以取到。

再考虑边界情况，即第一个元素若是目标值怎么办?这里推导一下上一步，如果$nums[left]==target, left=0$，那么$nums[mid]$必然等于$target$，且有$mid-1==left$，此时是满足第11行的判断条件的，所以$right=mid-1$（附带一句，此前$right==1$或$right==2$）。这样一来，得到新的$mid$值为$0$。所以，只要设定$mid$等于$0$时，返回$0$。见图4

 

这里还想讨论一下，是否需要考虑情况3，即$nums[mid]>target$?我的想法是，不需要。因为左半区间作为一个递增数组，右边界就已经是目标值了，那么左半区间的所有元素都只能小于和等于目标值。

 

右半区间的查找类似。代码如下

 1 private int right_binary_search(int[] nums, int left, int right, int target) {
 2     int mid = (left+right+1)>>1;
 3     int val = left;
 4     
 5     while(left<=right) {
 6         if(nums[mid]>target) {
 7             right=mid-1;
 8             mid=(left+right+1)>>1;
 9         }
10         else {
11             if(mid+1<nums.length&&nums[mid+1]==target) {
12                 left=mid+1;
13                 mid=(left+right+1)>>1;
14             }
15             else if (mid+1<nums.length&&nums[mid+1]!=target) {
16                 val = mid;
17                 break;
18             }
19             else if (mid+1==nums.length) {20                 return nums.length-1;
21             }        
22         }
23     }
24     return val;
25 }

 同样的，左边界就是PART1中的索引值，同时作为返回值$val$的初始值，该变量是最后输出的右边界。

考虑的情况也是类似的，分成两种情况（如图4）：

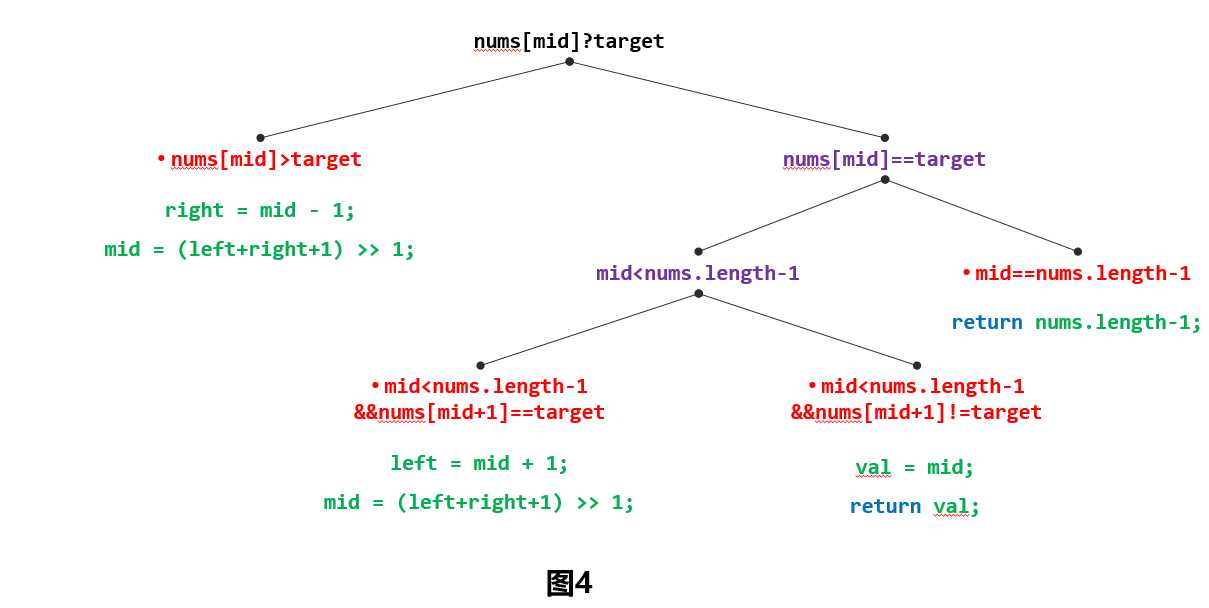
情况1，$nums[mid]>target$时，与之前的情况是相反的，所以此时应该移动右边界。

情况2，$nums[mid]==target$时，考虑情况也是类似的，只是数组越界的具体考虑不一样。我总结了一下，这里可以这么考虑，正常情况下，$mid$是可以取值$length-1$的，所以是mid $leq$ nums.length $-1$。那么由于考虑到$mid+1$的越界情况，所以$mid<nums.length - 1$

在边界条件上的考虑，也是类似的，故在此不再赘述。

 

最后是主函数的代码

 1 public int[] searchRange(int[] nums, int target) {
 2     int[] range = {-1,-1};
 3     if(nums == null || nums.length < 1)
 4         return range;
 5     
 6     
 7     int left = 0, right = nums.length-1;
 8     int mid;
 9     int leftborder, rightborder;
10     
11     int[] borders = locate(nums, left, right, target);
12     left=borders[0];right=borders[1];mid=borders[2];
13     
14     if (mid != -1) {
15         leftborder = left_binary_search(nums, left, mid, target);
16         rightborder = right_binary_search(nums, mid, right, target);
17         range[0]=leftborder;
18         range[1]=rightborder;
19     }
20 
21     return range;
22 }

 这里看到第14行，如果在第一次二分查找定位索引时，就没有找到，那么自然返回$-1$ ，于是就没有再进行左右区间分别查找的必要了（我突然在想，这部分其实可以是同时执行？）；反之，在左右区间得到的左右边界（也可呢就是第一部分查找得到的索引值）就是输出的范围。

---

  

总结：

• 对所有的情况要穷尽
• 考虑数组越界的可能要好好推导
• 对于边界条件要举例分析
• 对二分查找的认识更深入（指针移动，对半快速搜索）