kd-tree

Posted 2021-03-22 furujia

点云的搜索kdtree太重要，想要从头手撸一个枝叶分离的代码，所以开始吧。

参考：

https://zhuanlan.zhihu.com/p/45346117

https://leileiluoluo.com/posts/kdtree-algorithm-and-implementation.html

http://pointclouds.org/documentation/tutorials/kdtree_search.php

建立kdtree的步骤：

1. 建立根节点；

2. 选取方差最大的特征作为分割特征；

3. 选择该特征的中位数作为分割点；

4. 将数据集中该特征小于中位数的传递给根节点的左儿子，大于中位数的传递给根节点的右儿子；

5. 递归执行步骤2-4，直到所有数据都被建立到KD Tree的节点上为止。

 

查找最近邻步骤：

 

1. 从根节点开始，根据目标在分割特征中是否小于或大于当前节点，向左或向右移动。

 

2. 一旦算法到达叶节点，它就将节点点保存为“当前最佳”。

 

3. 回溯，即从叶节点再返回到根节点

 

4. 如果当前节点比当前最佳节点更接近，那么它就成为当前最好的。

 

5. 如果目标距离当前节点的父节点所在的将数据集分割为两份的超平面的距离更接近，说明当前节点的兄弟节点所在的子树有可能包含更近的点。因此需要对这个兄弟节点递归执行1-4步

 

建树例子：

以二维平面点(x,y)的集合(2,3)，(5,4)，(9,6)，(4,7)，(8,1)，(7,2)为例

a）构建根节点时，此时的切分维度为x，如上点集合在x维从小到大排序为(2,3)，(4,7)，(5,4)，(7,2)，(8,1)，(9,6)；其中值为(7,2)。（注：2,4,5,7,8,9在数学中的中值为(5 + 7)/2=6，但因该算法的中值需在点集合之内，所以本文中值计算用的是len(points)//2=3, points[3]=(7,2)）
b）(2,3)，(4,7)，(5,4)挂在(7,2)节点的左子树，(8,1)，(9,6)挂在(7,2)节点的右子树。
c）构建(7,2)节点的左子树时，点集合(2,3)，(4,7)，(5,4)此时的切分维度为y，中值为(5,4)作为分割平面，(2,3)挂在其左子树，(4,7)挂在其右子树。
d）构建(7,2)节点的右子树时，点集合(8,1)，(9,6)此时的切分维度也为y，中值为(9,6)作为分割平面，(8,1)挂在其左子树。至此k-d tree构建完成。

 

 

 

 

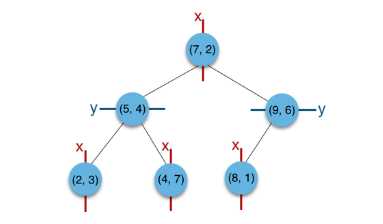
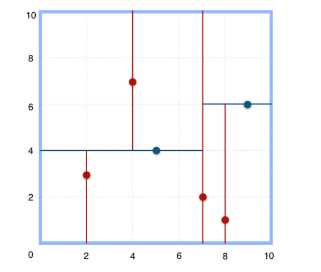
上述的构建过程结合下图可以看出，构建一个k-d tree即是将一个二维平面逐步划分的过程。

 

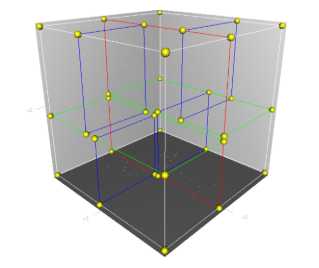
 我们还可以结合下图（该图引自维基百科），从三维空间来看一下k-d tree的构建及空间划分过程。
首先，边框为红色的竖直平面将整个空间划分为两部分，此两部分又分别被边框为绿色的水平平面划分为上下两部分。最后此4个子空间又分别被边框为蓝色的竖直平面分割为两部分，变为8个子空间，此8个子空间即为叶子节点。

 

PCL中的使用：

 1 #include <pcl/point_cloud.h>
 2 #include <pcl/kdtree/kdtree_flann.h>
 3 
 4 #include <iostream>
 5 #include <vector>
 6 #include <ctime>
 7 
 8 int
 9 main (int argc, char** argv)
10 {
11   srand (time (NULL));
12 
13   pcl::PointCloud<pcl::PointXYZ>::Ptr cloud (new pcl::PointCloud<pcl::PointXYZ>);
14 
15   // Generate pointcloud data
16   cloud->width = 1000;
17   cloud->height = 1;
18   cloud->points.resize (cloud->width * cloud->height);
19 
20   for (std::size_t i = 0; i < cloud->points.size (); ++i)//随机的点云
21   {
22     cloud->points[i].x = 1024.0f * rand () / (RAND_MAX + 1.0f);
23     cloud->points[i].y = 1024.0f * rand () / (RAND_MAX + 1.0f);
24     cloud->points[i].z = 1024.0f * rand () / (RAND_MAX + 1.0f);
25   }
26 
27   pcl::KdTreeFLANN<pcl::PointXYZ> kdtree;
28 
29   kdtree.setInputCloud (cloud);
30 
31   pcl::PointXYZ searchPoint;//随机的搜寻起始点
32 
33   searchPoint.x = 1024.0f * rand () / (RAND_MAX + 1.0f);
34   searchPoint.y = 1024.0f * rand () / (RAND_MAX + 1.0f);
35   searchPoint.z = 1024.0f * rand () / (RAND_MAX + 1.0f);
36 
37   // K nearest neighbor search
38 
39   int K = 10;
40 
41   std::vector<int> pointIdxNKNSearch(K);
42   std::vector<float> pointNKNSquaredDistance(K);//一次性定义三个跟K相关的东西
43 
44   std::cout << "K nearest neighbor search at (" << searchPoint.x 
45             << " " << searchPoint.y 
46             << " " << searchPoint.z
47             << ") with K=" << K << std::endl;
48 
49   if ( kdtree.nearestKSearch (searchPoint, K, pointIdxNKNSearch, pointNKNSquaredDistance) > 0 )
50   {
51     for (std::size_t i = 0; i < pointIdxNKNSearch.size (); ++i)
52       std::cout << "    "  <<   cloud->points[ pointIdxNKNSearch[i] ].x 
53                 << " " << cloud->points[ pointIdxNKNSearch[i] ].y 
54                 << " " << cloud->points[ pointIdxNKNSearch[i] ].z 
55                 << " (squared distance: " << pointNKNSquaredDistance[i] << ")" << std::endl;
56   }
57 
58   // Neighbors within radius search
59 
60   std::vector<int> pointIdxRadiusSearch;
61   std::vector<float> pointRadiusSquaredDistance;
62 
63   float radius = 256.0f * rand () / (RAND_MAX + 1.0f);//三个跟R相关的结构
64 
65   std::cout << "Neighbors within radius search at (" << searchPoint.x 
66             << " " << searchPoint.y 
67             << " " << searchPoint.z
68             << ") with radius=" << radius << std::endl;
69 
70 
71   if ( kdtree.radiusSearch (searchPoint, radius, pointIdxRadiusSearch, pointRadiusSquaredDistance) > 0 )
72   {
73     for (std::size_t i = 0; i < pointIdxRadiusSearch.size (); ++i)
74       std::cout << "    "  <<   cloud->points[ pointIdxRadiusSearch[i] ].x 
75                 << " " << cloud->points[ pointIdxRadiusSearch[i] ].y 
76                 << " " << cloud->points[ pointIdxRadiusSearch[i] ].z 
77                 << " (squared distance: " << pointRadiusSquaredDistance[i] << ")" << std::endl;
78   }
79 
80 
81   return 0;
82 }

运行结果：

 

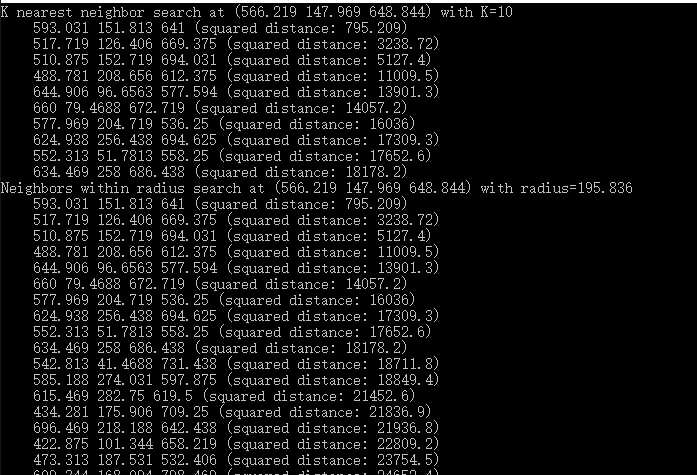
 这里有两个近邻查找，一个是查找最近的K个点（我们叫他K最近邻），一个是查找距离在某个范围（某个半径R）之内的点（我们叫他R最近邻）

K:离searchpoint最近的K个点

R:跟searchpoint在R范围内的点