CSP2019 树上的数 题解

Posted 2021-03-21 lishuyu2003

题面
这是一道典型的部分分启发正解的题。

所以我们先来看两个部分分。

Part 1 菊花图

这应该是除了暴力以外最好想的一档部分分了。

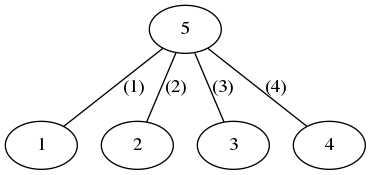
如上图（节点上的数字已省略），如果我们依次删去边(2)(1)(3)(4)，那么操作完后2号点上的数字就会跑到1号点上，1号点数字会跑到3号点上，3号点数字跑到4号点上……依此累推。那么我们相当于把五个节点连成了一个环( 5 -> 2 -> 1 -> 3 -> 4 -> 5 )，每一个结点上的数字都会跑到环上的下一个结点上去，我们就是要求能使最终得到的排列字典序最小的环。那么我们逐位贪心，先由数字1所在的节点选择它在环上的下一个点是哪一个，在由数字2所在节点选，依此类推。每次在合法的情况下选标号最小的节点即可。具体细节可以见代码。

Part1 代码:

#include<bits/stdc++.h>
using namespace std;
#define N 4007
#define mem(x) memset(x,0,sizeof(x))
int p[N],ans[N],vis[N];
int fa[N];
int find(int x)
{
    return fa[x]==x?x:fa[x]=find(fa[x]);
}
int main()
{
    int n,t;
    scanf("%d",&t);
    while(t--)
    {
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        fa[i]=i;
    mem(vis);
    for(int i=1;i<=n;i++)
        scanf("%d",&p[i]);
    int x,y;
    for(int i=1;i<n;i++)
        scanf("%d%d",&x,&y);
    for(int i=1;i<=n;i++)
    {
        int x=p[i];
        for(int j=1;j<=n;j++)
        {
        if(!vis[j]&&(i==n||find(x)!=find(j)))
        {
            ans[i]=j;
            fa[find(x)]=find(j);
            vis[j]=1;
            break;
        }
        }
    }
    for(int i=1;i<=n;i++)
        printf("%d ",ans[i]);
    printf("
");
    }
    return 0;
}

Part2 链

这一部分和正解关系紧密，引入了拓扑序的模型来描述题目中的限制条件。

其中节点中括号里的是节点上的数字。
如果数字1想跑到1号节点上去要怎么办？
那么我们可以依次删去(2)(3)号边，那么数字1就在1号点上了。
只要这样就可以了吗？
其实这里还隐含了两个条件，就是边(1)必须在(2)之后删除，且(4)必须在(3)之前删除，不然数字1就不在它应该在的地方了。
如果我们为每一条边定一个优先级，优先级大的先删，那么4条边的优先级大小关系就是：(1) < (2) > (3) < (4)
这样我们就可以保证数字1最终在1号点上了，此外因为我们要逐位贪心，所以在此基础上我们还希望数字2能到2号节点上。
但这是否有可能呢？
发现这样是不可能的，因为要使数字2到达2号点，那么必须满足优先级(3) > (2) ， 与数字1的条件是冲突的，所以不行。
所以我们得到了这部分的算法：
从数字1到数字n逐位贪心，每次选择一个当前数字能到达的、不与之前条件冲突的、标号最小的节点，作为这个数字最终所在的节点。然后将新产生的条件加入。
具体的实现可以在每一个节点上维护一个标记值0,1,2，分别表示这个节点左右的两条边之间的优先级 没有限制、左边大于右边、右边大于左边。然后每次从当前数字所在位置向左右两边找符合条件的点，再把新条件对应的标记值更新即可。具体见代码。

Part2 代码：

#include<bits/stdc++.h>
using namespace std;
#define N 4007
int hd[N],pre[N],to[N],num,tag[N],pos[N],id[N],p[N],d[N],cnt,ans[N];
void adde(int x,int y)
{
    num++;pre[num]=hd[x];hd[x]=num;to[num]=y;
}
void dfs(int v,int f)
{
    id[++cnt]=v,pos[v]=cnt;
    for(int i=hd[v];i;i=pre[i])
    {
    int u=to[i];
    if(u==f)continue;
    dfs(u,v);
    }
}
#define mem(x) memset(x,0,sizeof(x))
int main()
{
    int n;
    int t;
    scanf("%d",&t);
    while(t--)
    {
    scanf("%d",&n);
    mem(hd),mem(tag),mem(d);
    num=0,cnt=0;
    for(int i=1;i<=n;i++)
        scanf("%d",&p[i]);
    for(int i=1;i<n;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        adde(x,y),adde(y,x);
        d[x]++,d[y]++;
    }
    int rt=0;
    for(int i=1;i<=n ;i++)
        if(d[i]==1)rt=i;
    dfs(rt,0);
    for(int i=1;i<=n;i++)
    {#include<bits/stdc++.h>
using namespace std;
#define N 20007
#define mem(x) memset(x,0,sizeof(x))
int hd[N],pre[N],to[N],num,fa[N],sz[N],d[N],p[N],ver;
bool in[N],out[N];
void adde(int x,int y)
{
    num++;pre[num]=hd[x];hd[x]=num;to[num]=y;
}
int find(int x)
{
    return fa[x]==x?x:fa[x]=find(fa[x]);
}
void merge(int x,int y)
{
    int u=find(x),v=find(y);
    fa[u]=v,sz[v]+=sz[u];
    out[x]=in[y]=1;
}
bool check(int x,int y,int l)
{
    if(in[y]||out[x])return false;
    int u=find(x),v=find(y);
    if(u==v&&sz[u]!=l)return false;
    return true;
}
void dfs1(int v,int f)
{
    if(f!=v&&check(f,v,d[v]+1))ver=min(ver,v);
    for(int i=hd[v];i;i=pre[i])
    {
    int u=to[i];
    if(i==f)continue;
    if(check(f,i,d[v]+1))
    {
        dfs1(u,i^1);
    }
    }
}
bool dfs2(int v,int f,int p)
{
    if(v==p)
    {
    merge(f,v);
    return true;
    }
    for(int i=hd[v];i;i=pre[i])
    {
    int u=to[i];
    if(i==f)continue;
    if(dfs2(u,i^1,p))
    {
        merge(f,i);
        return true;
    }
    }
    return false;
}
int main()
{
    int t,n;
    scanf("%d",&t);
    while(t--)
    {
    scanf("%d",&n);
    mem(hd),mem(in),mem(out),mem(d);
    num=(n+1)/2*2+1;
    for(int i=1;i<=n;i++)
        scanf("%d",&p[i]);
    for(int i=1;i<n;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        d[x]++,d[y]++;
        adde(x,y),adde(y,x);
    }
    for(int i=1;i<=num;i++)
        fa[i]=i,sz[i]=1;
    for(int i=1;i<=n;i++)
    {
        int v=p[i];
        ver=n+1;
        dfs1(v,v);
        dfs2(v,v,ver);
        printf("%d ",ver);
    }
    printf("
");
    }
    return 0;
}

        int x=p[i],b=pos[x];
        int mi=n+1;
        if(tag[b]!=1)
        {
        for(int j=b+1;j<=n;j++)
        {
            if(tag[j]!=1)mi=min(mi,id[j]);
            if(tag[j]==2)break;
        }
        }
        if(tag[b]!=2)
        {
        for(int j=b-1;j>=1;j--)
        {
            if(tag[j]!=2)mi=min(mi,id[j]);
            if(tag[j]==1)break;
        }
        }
        if(pos[mi]>b)
        {
        for(int j=b+1;j<=pos[mi]-1;j++)tag[j]=1;
        tag[b]=tag[pos[mi]]=2;
        }
        else
        {
        for(int j=pos[mi]+1;j<b;j++)tag[j]=2;
        tag[pos[mi]]=tag[b]=1;
        }
        tag[1]=tag[n]=0;
        ans[i]=mi;
    }
    for(int i=1;i<=n;i++)
        printf("%d ",ans[i]);
    printf("
");
    }
    return 0;
}

Part3 正解

其实从第二部分我们已经看到，形如数字x要到y号节点上所需满足的条件可以描述为一系列边的优先级的大小关系（这里的优先级实际上就是一种拓扑序），并且我们可以把这些条件放在节点上，表示与这个节点相邻的所有边之间的大小关系是怎样的，也就是说只有与同一个节点相邻的边之间才会有大小关系的限制。那么我们如何把链上的算法拓展到一般的树上呢？

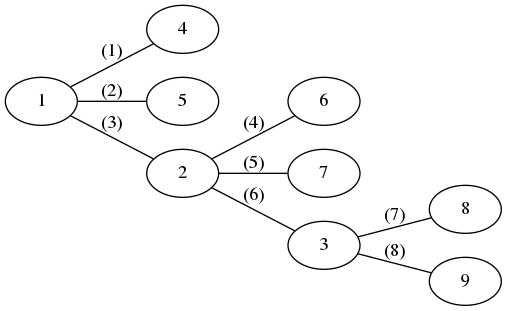
如果有一个数字想从1号点到3号点，那么需要满足的条件有两种：

1. (3)的优先级是与1号点相邻的边中最大的，(6)的优先级是与3号点相邻的边中最小的；
2. (3)的优先级大于(6)；

对于条件2，这样还不够充分，因为如果删完(3)之后再删(4)的话就不对了。也就是说删完(3)之后要紧接着删(6)
这个限制条件就相当于把与2号点相邻的边按照优先级大小排列，那么(3)和(6)必须是相邻的，且(3)在(6)前面。
怎么做到这一点呢？发现这种要让两条边相邻的条件其实已经在第一部分的菊花图中讨论过了，一样的用并查集判断即可，只不过Part1中只用了一个并查集，而现在我们要维护每一个点周围的边的大小关系，所以要对每一个点开一个并查集。
而对于条件1，我的做法是对每一个并查集建了一个虚点，如果一条边的优先级最大，那么由虚点向它连一条边，如果一条边优先级最小，则由它向虚点连一条边，这样就可以直接套Part1部分的代码了。
然后贪心过程与Part2类似，每次从一个点出发遍历整棵树，每走一条边就判断一下，然后再对一条路径进行修改即可。

Part3 代码：

#include<bits/stdc++.h>
using namespace std;
#define N 20007
#define mem(x) memset(x,0,sizeof(x))
int hd[N],pre[N],to[N],num,fa[N],sz[N],d[N],p[N],ver;
bool in[N],out[N];
void adde(int x,int y)
{
    num++;pre[num]=hd[x];hd[x]=num;to[num]=y;
}
int find(int x)
{
    return fa[x]==x?x:fa[x]=find(fa[x]);
}
void merge(int x,int y)
{
    int u=find(x),v=find(y);
    fa[u]=v,sz[v]+=sz[u];
    out[x]=in[y]=1;
}
bool check(int x,int y,int l)
{
    if(in[y]||out[x])return false;
    int u=find(x),v=find(y);
    if(u==v&&sz[u]!=l)return false;
    return true;
}
void dfs1(int v,int f)
{
    if(f!=v&&check(f,v,d[v]+1))ver=min(ver,v);
    for(int i=hd[v];i;i=pre[i])
    {
    int u=to[i];
    if(i==f)continue;
    if(check(f,i,d[v]+1))
    {
        dfs1(u,i^1);
    }
    }
}
bool dfs2(int v,int f,int p)
{
    if(v==p)
    {
    merge(f,v);
    return true;
    }
    for(int i=hd[v];i;i=pre[i])
    {
    int u=to[i];
    if(i==f)continue;
    if(dfs2(u,i^1,p))
    {
        merge(f,i);
        return true;
    }
    }
    return false;
}
int main()
{
    int t,n;
    scanf("%d",&t);
    while(t--)
    {
    scanf("%d",&n);
    mem(hd),mem(in),mem(out),mem(d);
    num=(n+1)/2*2+1;
    for(int i=1;i<=n;i++)
        scanf("%d",&p[i]);
    for(int i=1;i<n;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        d[x]++,d[y]++;
        adde(x,y),adde(y,x);
    }
    for(int i=1;i<=num;i++)
        fa[i]=i,sz[i]=1;
    for(int i=1;i<=n;i++)
    {
        int v=p[i];
        ver=n+1;
        dfs1(v,v);
        dfs2(v,v,ver);
        printf("%d ",ver);
    }
    printf("
");
    }
    return 0;
}

总结：通过这题大家可以发现，此题正解与部分分是紧密相连的，如果没有对部分分的思考，很难直接想到正解。这启发我们当无法直接想到正解时，可以思考一些此题的部分分，找到部分分与正解之间的联系，进而以迂回的方式找到正解。一些人因过于追求正解，直接跳过部分分思考正解，结果反而无法得到正解。比如本文作者就是这样一个反面例子