车联网 - 电子围栏技术

Posted 2020-11-16 xtuz

什么是汽车电子围栏

通常来说，电子围栏是管理者事先划定好一块规则或不规则的区域，也可以按照行政区域进行划分，例如北京市、广东省等。

其目的是为了便于管理：车辆驶离指定的区域，系统会按事先设定的条件，启动相关的处理程序，及时向车队管理者发出警报及手机端会推送通知。

工作流程

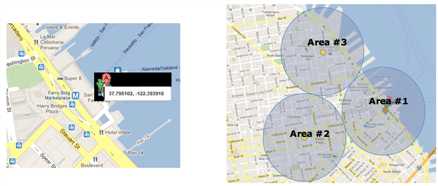
1. 车载设备需要安装GPS设备，并能实时定位当前位置主动上报。
2. 管理者在TSP系统中设定车辆行驶在哪一个指定区域里，并制定出当车辆驶出指定区域后的解决方案。
3. 车辆通过4G/5G通讯网络传输当前车辆位置信息TSP系统，系统存储车辆w位置数据和并进行实时分析，记录和备份车辆的行驶路径。
4. 如果车辆驶出设定的指定区域，TSP系统则推送警报给管理者以告知。

电子围栏算法

1. 射线法

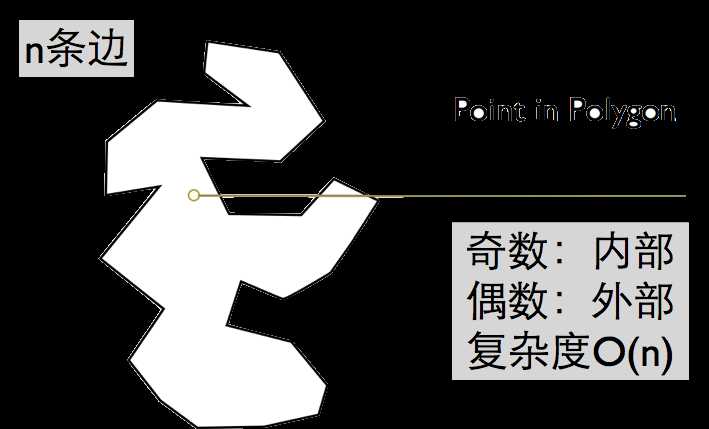
地理围栏一般是多边形，如何判断点在多边形内部呢？可以通过射线法来判断点是否在多边形内部。如下图所示，从该点出发沿着X轴画一条射线，依次判断该射线与每条边的交点，并统计交点个数，如果交点数为奇数，则在多边形内部（如图3个交点），如果焦点数是偶数，则在外部，射线法对凸和非凸多边形都适用，复杂度为O(N)。

2. 夹角和法

如图 1.4，在多边形内或外有一点，将这一点与多边形的各个角相连，构成夹角，为 <1、 <2 、<3、<4 、<5 和 <6 ，把这些夹角相加便得到夹角和，为方便起见，记此夹角和为 a。规定正向为顺时针旋转方向，负向为逆时针方向[4]。当 a！=2π 时，则被判断点在多边形 的外部；当 a=2π 时，则被判断点在多边形的内部。

夹角和法只可以用于凸多边形，然而围栏形状是多变的，可能是凸多边形也可能 是凹多边形。从解决问题的广度上来说，射线法是最适合的方法。

代码示例

import json
import math
lnglatlist = []

data = '[{"points":[{"lng":0,"lat":0},{"lng":2,"lat":0},{"lng":0,"lat":2}]}]'

data = json.loads(data)
if 'points' in data[0]:
    for point in data[0]['points']:
        lnglat = []
        lnglat.append(float(str(point['lng'])))
        lnglat.append(float(str(point['lat'])))
        lnglatlist.append(lnglat)

def windingNumber(point, poly):
    poly.append(poly[0])
    px = point[0]
    py = point[1]
    sum = 0
    length = len(poly)-1

    for index in range(0,length):
        sx = poly[index][0]
        sy = poly[index][1]
        tx = poly[index+1][0]
        ty = poly[index+1][1]

        #点与多边形顶点重合或在多边形的边上
        if((sx - px) * (px - tx) >= 0 and (sy - py) * (py - ty) >= 0 and (px - sx) * (ty - sy) == (py - sy) * (tx - sx)):
            return "on"
        #点与相邻顶点连线的夹角
        angle = math.atan2(sy - py, sx - px) - math.atan2(ty - py, tx - px)
        #确保夹角不超出取值范围（-π 到 π）
        if(angle >= math.pi):
            angle = angle - math.pi * 2
        elif(angle <= -math.pi):
            angle = angle + math.pi * 2
        #计算回转数并判断点和多边形的几何关系
    result = 'out' if int(sum / math.pi) == 0 else 'in'
    return result

point = [1, 1]
print(windingNumber(point,lnglatlist))

---

更多内容参考 >> 电子围栏技术详解