Codeforces Round #609 (Div. 2)

Posted 2021-03-21 heyuhhh

传送门

A. Equation

签到。

Code

/*
 * Author:  heyuhhh
 * Created Time:  2019/12/21 19:07:29
 */
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
  #define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
  void err() { std::cout << '
'; }
  template<typename T, typename...Args>
  void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
#else
  #define dbg(...)
#endif
void pt() {std::cout << '
'; }
template<typename T, typename...Args>
void pt(T a, Args...args) {std::cout << a << ' '; pt(args...); }
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 1e5 + 5;
 
int n;
 
bool ok(ll x) {
    for(int i = 2; 1ll * i * i <= x; i++) {
        if(x % i == 0) return true;
    }   
    return false;
}
 
void run(){
    for(ll i = 4;; i++) {
        if(ok(i) && ok(i + n)) {
            cout << i + n << ' ' << i << '
';
            return;
        }   
    }
}
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cout << fixed << setprecision(20);
    while(cin >> n) run();
    return 0;
}

B. Modulo Equality

因为(n)比较小，直接枚举循环排列然后check即可。

Code

/*
 * Author:  heyuhhh
 * Created Time:  2019/12/21 20:39:59
 */
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
  #define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
  void err() { std::cout << '
'; }
  template<typename T, typename...Args>
  void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
#else
  #define dbg(...)
#endif
void pt() {std::cout << '
'; }
template<typename T, typename...Args>
void pt(T a, Args...args) {std::cout << a << ' '; pt(args...); }
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 2000 + 5;
 
int n, m;
int a[N], b[N];
 
void run(){
    for(int i = 1; i <= n; i++) cin >> a[i];
    for(int i = 1; i <= n; i++) cin >> b[i];
    sort(a + 1, a + n + 1);
    sort(b + 1, b + n + 1);
    int ans = INF;
    for(int i = 0; i < n; i++) {
        int x = -1, ok = 1;
        for(int j = 1; j <= n; j++) {
            int p = j, q = (j + i - 1) % n + 1;
            int d = (b[p] - a[q] + m) % m;
            if(x == -1) x = d;
            else if(x != d) ok = 0;
        }   
        if(ok) ans = min(ans, x);
    }
    cout << ans << '
';
}
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cout << fixed << setprecision(20);
    while(cin >> n >> m) run();
    return 0;
}

C. Long Beautiful Integer

题意：
给出一个长度为(n,nleq 2e5)的十进制数(x)。
然后要找到一个最小的数(y)，满足(ygeq x)且(y_i=y_{i+k},ileq n-k)。

思路：
对于(x)来说，若第一次出现(x_i ot ={x_{i+k}})的位置满足(x_i>x_{i+k})，那么直接显然(x_{i+k}=x_i)。
然后有这样一个性质：

• 若当前为第(i)个位置，并且(x_i)增大，那么(i+1)~(n)的位置上面的值都可以随便填。

这个较为显然。所以在上面说的情况，因为(x_{i+k})增大了，那么后面直接等于前面相应位置即可。

如果第一次出现的为(x_i<x_{i+k})，我们就需要另外考虑。
显然我们只需要在(1)~(k)的位置找一个值进行增大，因为对应位置必须相等，若在后面增大的话，前面的也会跟着增大。并且因为要求(y)最小，所以我们从(k)往前来进行增大，若某个位置增加，那么后面的都可以等于前面的。
为什么说是从后往前呢？不是只选一个位置增大就行了么？
因为要考虑(8999cdots)这种需要进位的情况。
细节见代码：

Code

/*
 * Author:  heyuhhh
 * Created Time:  2019/12/22 10:13:49
 */
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
  #define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
  void err() { std::cout << '
'; }
  template<typename T, typename...Args>
  void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
#else
  #define dbg(...)
#endif
void pt() {std::cout << '
'; }
template<typename T, typename...Args>
void pt(T a, Args...args) {std::cout << a << ' '; pt(args...); }
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 2e5 + 5;
 
int n, k;
string s;
 
void run(){
    cin >> s;
    cout << n << '
';
    string p = s;
    s = s.substr(0, k);
    string t = s;
    int len = k;
    for(;len < n;) s += t, len += k;   
    s = s.substr(0, n);
    if(s >= p) {
        cout << s << '
';
        return;
    }
    for(int i = k - 1; i >= 0; i--) {
        if(s[i] == '9') s[i] = '0';
        else {
            s[i] += 1;
            break;
        }   
    }
    for(int i = k; i < n; i++) s[i] = s[i - k];
    cout << s << '
';
}
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cout << fixed << setprecision(20);
    while(cin >> n >> k) run();
    return 0;
}

D. Domino for Young

题意：
给出(n)列高度为(a_i)的格子，类似于下面：

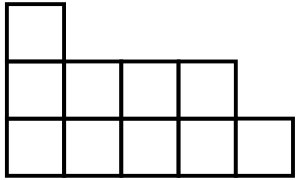
现在要用(1 imes 2)的多米诺骨牌来填充。问最多可以放置多少个这样的多米诺骨牌。

思路：
我们直接将给出的图黑白染色，那么答案就是
[ min(黑色格子数量，白色格子数量) ]
至于为啥，我也不清楚= =

Code

/*
 * Author:  heyuhhh
 * Created Time:  2019/12/22 10:32:59
 */
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
  #define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
  void err() { std::cout << '
'; }
  template<typename T, typename...Args>
  void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
#else
  #define dbg(...)
#endif
void pt() {std::cout << '
'; }
template<typename T, typename...Args>
void pt(T a, Args...args) {std::cout << a << ' '; pt(args...); }
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 3e5 + 5;
 
int n;
int a[N];
ll cnt[2];
 
void run(){
    for(int i = 1; i <= n; i++) cin >> a[i];
    for(int i = 1; i <= n; i++) {
        cnt[i & 1] += (a[i] + 1) / 2;
        cnt[!(i & 1)] += a[i] / 2;   
    }
    ll ans = min(cnt[0], cnt[1]);
    cout << ans << '
';
}
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cout << fixed << setprecision(20);
    while(cin >> n) run();
    return 0;
}