连通性问题

Posted 2021-03-20 g1191613819

一、问题引出

现在有多个尚未连通的城市A、B、C...，现在政府要在每个城市修建高速公路，使每个城市都连通起来。但是呢，由于今年的财政收入赤字，没有过多的预算，所以决定在每连通两个城市的时候判断一下，这两城市到底是不是互通的，以此来节省费用。比如：已经修建了A-B、B-C之间的道路，那么在判断A-C的时候，由于A和C都连接B，那么A-C是互通的，就不需要再修建道路。很多人在第一眼看到这个问题的时候，会感觉非常的棘手，毕竟有一些隐藏的连通关系需要自己去判断。

二、解法

①快速查找算法

#include <stdio.h>
#define N 10000

void main()
{
    int array[N],x,y,i,j,temp;
    //初始化数组
    for(i=0;i<N;i++)
        array[i]=i;
    while(scanf("%d-%d",&x,&y)==2){
        //如果两个值相等，说明两点连通
        if(array[x]==array[y])
            continue;
        for(temp=array[x],j=0;j<N;j++)
            //将x点连通的所有的点，也连通y。这里无论是统一成array[x]或者array[y]的值均可。
            if(array[j]==temp)
                array[j]=array[y];
        //打印出需要连通的点对
        printf("需要连通的点对：%d-%d
",x,y);
    }
}

结果：

 分析：数组索引表示不同城市，数组存放的值则用来指代是否连通。①一开始数组初始化为各自的索引（代表所有城市均未连通）②然后等待输入点对。③首先判断该点对（数组索引）存放的值是否相同。如果相同，则说明两点连通，继续等待输入；反之，将x点所有连通的点再连通y(即存放的值统一即可)。最后重复②③步骤

缺点：M次合并操作（输入次数），N个点所需要执行的指令数MN

②快速合并算法

#include <stdio.h>
#define N 10000

void main()
{
    int array[N],x,y,i,j;
    //初始化数组
    for(i=0;i<N;i++)
        array[i]=i;
    while(scanf("%d-%d",&x,&y)==2){
       //构造树
       //寻找x的根节点，只有当索引和对应存储的值相同的时候，该点才是该树的根节点
       for(i=x;i!=array[i];i=array[i]);
       //寻找y的根节点
       for(j=y;j!=array[j];j=array[j]);
       //根节点为同一个，说明俩点连通
       if(i==j)
        continue;
       //将x所在的树合并到y所在的树上
       array[i]=j;
       printf("所需要连通的点对：%d-%d
",x,y);
    }
}

结果：

分析：

①用图形表示整个流程：

1）初始：

（数组里的值）

0 1 2 3 4

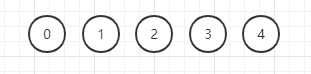
2）输入1-2，1的树连接到2的树上

0 2 2 3 4

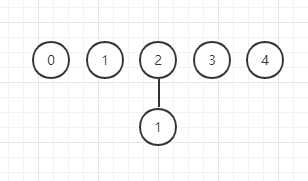
3）输入2-3，2的树连接到3的树上

0 2 3 3 4

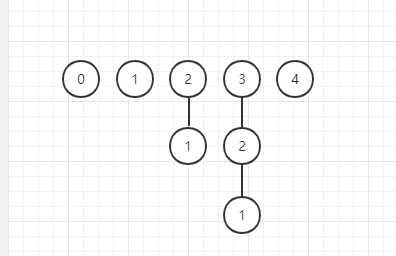
4）输入1-3，发现1-3已经连通，不操作；输入3-4，将3的树连接到4的树上 

0 2 3 4 4

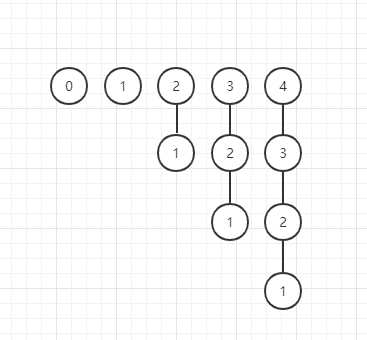
5）输入1-4、2-4，均已连通，不操作

0 2 3 4 4

 

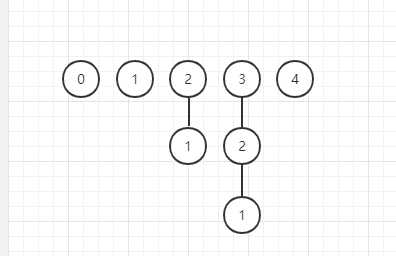
②输入点对过后，根据点向上找对应的根节点（如果两点是连通的，那么必定其根节点必定是同一个），来判断两点是否连通。如果连通，那么不操作；反之，将第一个点的树合并到第二个点的树上

缺点：可能会造成树的层越来越高，而这主要是由于合并操作的时候都是简单的把前者的树合并到后者上

 

③加权快速合并算法

#include <stdio.h>
#define N 10000

void main()
{
    int num[N],array[N],x,y,i,j;
    //初始化数组
    for(i=0;i<N;i++)
        array[i]=i;
    for(i=0;i<N;i++)
        num[i]=1;
    while(scanf("%d-%d",&x,&y)==2){
       //构造树
       //寻找x的根节点，只有当索引和对应存储的值相同的时候，该点才是该树的根节点
       for(i=x;i!=array[i];i=array[i]);
       //寻找y的根节点
       for(j=y;j!=array[j];j=array[j]);
       //根节点为同一个，说明俩点连通
       if(i==j)
        continue;
       //合并
       //x的树大，将y合并到x上
       if(num[i]>num[j]){
        array[j]=i;
        num[i]+=num[j];
       }
       //y的树大，将x合并到y上
       else {
        array[i]=j;
        num[j]+=num[i];
       }
       printf("所需要连通的点对：%d-%d
",x,y);
    }
}

结果：

 分析：

只需要多一个辅助记录（树的节点个数）的数组，在每次合并树的时候判断哪边的树大（小树合并到大树上，会使树的高度尽可能低），合并完后在该树的根节点加上被合并的节点数

缺点：

节点到根节点的距离可能还是过长

 

④等分路径压缩算法  

#include <stdio.h>
#define N 10000

void main()
{
    int num[N],array[N],x,y,i,j;
    //初始化数组
    for(i=0;i<N;i++)
        array[i]=i;
    for(i=0;i<N;i++)
        num[i]=1;
    while(scanf("%d-%d",&x,&y)==2){
       //构造树
       //寻找x的根节点，只有当索引和对应存储的值相同的时候，该点才是该树的根节点
       for(i=x;i!=array[i];i=array[i]);
        array[i]=array[array[i]];
       //寻找y的根节点
       for(j=y;j!=array[j];j=array[j]);
        array[j]=array[array[j]];
       //根节点为同一个，说明俩点连通
       if(i==j)
        continue;
       //合并
       //x的树大，将y合并到x上
       if(num[i]>num[j]){
        array[j]=i;
        num[i]+=num[j];
       }
       //y的树大，将x合并到y上
       else {
        array[i]=j;
        num[j]+=num[i];
       }
       printf("所需要连通的点对：%d-%d
",x,y);
    }
}

分析：等分路径压缩其实就是在每次找点对的根节点的时候，将当前的那个节点指向他的爷爷节点，最终经过一次又一次达到节点都直接指向他们的根节点

①用图形表示整个流程：

首先有5个线性连通的点

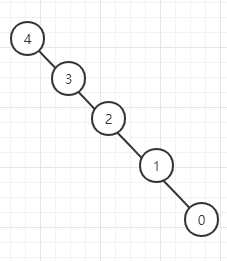
 当使用等分路径压缩后（当前节点指向自己的爷爷节点）

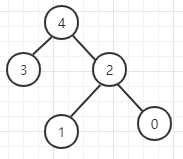
②用代码表示整个流程

#include <stdio.h>
#define N 10000

void main()
{
    int array[N],x,y,i,j;
    //初始化数组
    for(i=0;i<N;i++)
        array[i]=i;
    while(scanf("%d-%d",&x,&y)==2){
       //构造树
       //寻找x的根节点，只有当索引和对应存储的值相同的时候，该点才是该树的根节点
       for(i=x;i!=array[i];i=array[i])
            array[i]=array[array[i]];
       //寻找j的根节点
       for(j=y;j!=array[j];j=array[j])
            array[j]=array[array[j]];
       //根节点为同一个，说明俩点连通
       if(i==j)
        continue;
       //合并
       array[i]=array[j];
       printf("所需要连通的点对：%d-%d
",x,y);
       for(i=0;i<10;i++){
         printf("%d ",array[i]);
       }
       printf("
");
    }
}

结果：

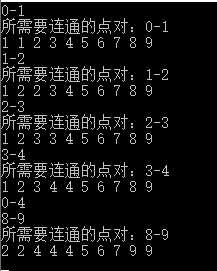
 能够很明显的看出来当执行0-4时，路径进行了压缩

1 2 3 4 4  ->  2 2 4 4 4

 

三、总结

最优的选择还是加权快速合并算法