逻辑回归

Posted 2021-03-20 xiaojingjingzhuanshu

逻辑回归(Logistic Regression)

在这节课中，我们会重温逻辑回归学习算法，该算法适用于二分类问题，本节将主要介绍逻辑回归的Hypothesis Function（假设函数）。

对于二元分类问题来讲，给定一个输入特征向量X，它可能对应一张图片，你想识别这张图片识别看它是否是一只猫或者不是一只猫的图片，你想要一个算法能够输出预测，你只能称之为y^（也就是预测值），也就是你对实际值 y 的估计。更正式地来说，你想让 y^ 表示 y 等于1的一种可能性或者是机会，前提条件是给定了输入特征X。换句话来说，如果X是我们在上个视频看到的图片，你想让 y ^来告诉你这是一只猫的图片的机率有多大。在之前的视频中所说的，X是一个n_x维的向量（相当于有n_x个特征的特征向量）。我们用w来表示逻辑回归的参数，这也是一个n_x维向量（因为w实际上是特征权重，维度与特征向量相同），参数里面还有b，这是一个实数（表示偏差）。所以给出输入x以及参数w和b之后，我们怎样产生输出预测值y^，一件你可以尝试却不知可不可行的事是让y^=(w^T) x+b。

 

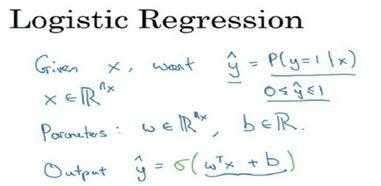
这时候我们得到的是一个关于输入x的线性函数，实际上这是你在做线性回归时所用到的，但是这对于二元分类问题来讲不是一个非常好的算法，因为你想让y^表示实际值y等于1的机率的话，y ^应该在0到1之间。这是一个需要解决的问题，因为(w^T)x+b可能比1要大得多，或者甚至为一个负值。对于你想要的在0和1之间的概率来说它是没有意义的，因此在逻辑回归中，我们的输出应该是^y等于由上面得到的线性函数式子作为自变量的sigmoid函数中，公式如上图最下面output所示，将线性函数转换为非线性函数（线性变成非线性函数，治这个手法要记得！也是一个重点的概念）。

Sigmoid函数

下图是sigmoid函数的图像，如果我把水平轴作为z轴，那么关于z的sigmoid函数是这样的，它是平滑地从0走向1，让我在这里标记纵轴，这是0，曲线与纵轴相交的截距是0.5，这就是关于z的sigmoid函数的图像。我们通常都使用z来表示(w^T) x+b的值。

 

 

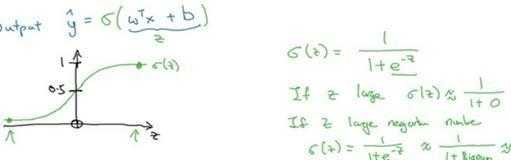
关于sigmoid函数的公式是这样的，σ(z)=1/(1+e^(-z) ),在这里z是一个实数，这里要说明一些要注意的事情，重点！仔细看了！

如果z非常大那么e^(-z)将会接近于0，关于z的sigmoid函数将会近似等于1除以1加上某个非常接近于0的项，因为e 的指数如果是个绝对值很大的负数的话，这项将会接近于0，所以如果z很大的话那么关于z的sigmoid函数会非常接近1。相反地，如果z非常小或者说是一个绝对值很大的负数，那么关于e^(-z)这项会变成一个很大的数，你可以认为这是1除以1加上一个非常非常大的数，所以这个就接近于0。实际上你看到当z变成一个绝对值很大的负数，关于z的sigmoid函数就会非常接近于0，

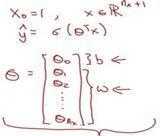
因此当你实现逻辑回归时，你的工作就是去让机器学习参数w以及b这样才使得y^成为对y=1这一情况的概率的一个很好的估计。

 

 

在继续进行下一步之前，介绍一种符号惯例，可以让参数w和参数b分开。在符号上要注意的一点是当我们对神经网络进行编程时经常会让参数w和参数b分开，在这里参数b对应的是一种偏置。在之前的机器学习课程里，你可能已经见过处理这个问题时的其他符号表示。比如在某些例子里，你定义一个额外的特征称之为x_0，并且使它等于1，那么现在X就是一个n_x加1维的变量，然后你定义y^=σ(θ^T x)的sigmoid函数。在这个备选的符号惯例里，你有一个参数向量θ_0,θ_1,θ_2,...,θ_(n_x )，这样θ_0就充当了b，这是一个实数，而剩下的θ_1 直到θ_(n_x )充当了w，结果就是当你实现你的神经网络时，有一个比较简单的方法是保持b和w分开。但是在这节课里我们不会使用任何这类符号惯例，所以不用去担心。

转自链接：https://www.jianshu.com/p/c37627a90d4c