ACM模板整理|2019/12/27

Posted 2021-03-19 fisherss

看到群里都是18、19级的学弟，才发现自己老了啊??
还算充实的一天，就是电影还没看。。

最短路

Floyd

应用
1.Floyd求有向图最小环：枚举g[i][i]
2.Floyd求无向图最小环：
if (f[k][i] && f[k][j] ) { ans = min(e[i][j]+2,ans); }

const int inf = 0x3f3f3f3f;
int g[MAX_N][MAX_N];  // 算法中的 G 矩阵
// 首先要初始化 g 矩阵
void init() {
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < n; ++j) {
            if (i == j) {
                g[i][j] = 0;
            } else {
                g[i][j] = inf;
            }
        }
    }    
}

// 插入一条带权有向边
void insert(int u, int v, int w) {
    g[u][v] = w;
}

// 核心代码
void floyd() {
    for (int k = 0; k < n; ++k) {
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                if (g[i][k] + g[k][j] < g[i][j]) {
                    g[i][j] = g[i][k] + g[k][j];
                }
            }
        }
    }    
}

int main(){
    //输入顶点个数//初始化//输入邻接矩阵
}

SPFA负权图最短路:

应用:
1.求负权图最短路
2.SPFA判断负环:每次入队 ++in[v]; if(in[v] > n) 存在负环

const int MAX_N = 10000;
const int MAX_M = 100000;
const int inf = 0x3f3f3f3f;
struct edge {
    int v, w, next;
} e[MAX_M];
int p[MAX_N], eid, n;
bool inq[MAX_N];
int d[MAX_N]; 
void mapinit() {
    memset(p, -1, sizeof(p));
    eid = 0;
}
void insert(int u, int v, int w) {  // 插入带权单向有向边
    e[eid].v = v;
    e[eid].w = w;
    e[eid].next = p[u];
    p[u] = eid++;
}
void spfa(int s) {
    memset(inq, 0, sizeof(inq));
    memset(d, 0x3f, sizeof(d));
    d[s] = 0;
    inq[s] = true;
    queue<int> q;
    q.push(s);
    while (!q.empty()) {
        int u = q.front();
        q.pop();
        inq[u] = false;
        for (int i = p[u]; i != -1; i = e[i].next) {
            int v = e[i].v;
            if (d[u] + e[i].w < d[v]) {
                d[v] = d[u] + e[i].w;
                if (!inq[v]) {
                    q.push(v);
                    inq[v] = true;
                }
            }
        }
    }
}

优先队列优化dijkstra

const int MAX_N = 10000;
const int MAX_M = 100000;
const int inf = 0x3f3f3f3f;
struct edge {
    int v, w, next;
} e[MAX_M];
int p[MAX_N], eid, n;
int dist[MAX_N];  // 存储单源最短路的结果
bool vst[MAX_N];  // 标记每个顶点是否在集合 U 中
struct node {// 记录点的结构体
    int u;
  int dist;
    node(int _u, int _dist) : u(_u), dist(_dist) {}
    bool operator < (const node &x) const {
        return dist > x.dist;
    }
}; 
bool dijkstra(int s) {
    // 初始化 dist、小根堆和集合 U
    memset(vst, 0, sizeof(vst));
    memset(dist, 0x3f, sizeof(dist));
    priority_queue<node> min_heap;
    dist[s] = 0;
    min_heap.push(node(s, 0));
    while (!min_heap.empty())
        // 获取堆顶元素，并将堆顶元素从堆中删除
        int v = min_heap.top().u;
        min_heap.pop();
        if (vst[v]) continue;
        vst[v] = true;
        // 进行和普通 dijkstra 算法类似的松弛操作
        for (int j = p[v]; j != -1; j = e[j].next) {
            int x = e[j].v;
            if (!vst[x] && dist[v] + e[j].w < dist[x]) {
                dist[x] = dist[v] + e[j].w;
                min_heap.push(node(x, dist[x]));
            }
        }
    }
    return true;
}

普通dijkstra：

int dist[MAX_N];  // 存储单源最短路的结果
bool vst[MAX_N];  // 标记每个顶点是否在集合 U 中
bool dijkstra(int s) {
    memset(vst, 0, sizeof(vst));
    memset(dist, 0x3f, sizeof(dist));
    dist[s] = 0;
    for (int i = 0; i < n; ++i) {
        int v, min_w = inf;  // 记录 dist 最小的顶点编号和 dist 值
        for (int j = 0; j < n; ++j) {
            if (!vst[j] && dist[j] < min_w) {
                min_w = dist[j];
                v = j;
            }
        }
        if (min_w == inf) {  // 没有可用的顶点，算法结束，说明有顶点无法从源点到达
            return false;
        }
        vst[v] = true;  // 将顶点 v 加入集合 U 中
        for (int j = p[v]; j != -1; j = e[j].next) {
            // 如果和 v 相邻的顶点 x 满足 dist[v] + w(v, x) < dist[x] 则更新 dist[x]，这一般被称作“松弛”操作
            int x = e[j].v;
            if (!vst[x] && dist[v] + e[j].w < dist[x]) {
                dist[x] = dist[v] + e[j].w;
            }
        }
    }
    return true;  // 源点可以到达所有顶点，算法正常结束
}

差分和前缀和

一维差分数组

#include<cstdio>

int n,m,q;
int a[100000],d[100000],f[100000],sum[100000];

int main(){
    int x,y,z;
    scanf("%d %d %d",&n,&m,&q); //输入数据 
    for(int i=1;i<=n;i++){
        scanf("%d",&a[i]);
        d[i]=a[i]-a[i-1]; //求d[i]数组 
    }
    
    //m个操作 [x,y]区间增加z 
    for(int i=1;i<=m;i++){
        scanf("%d %d %d",&x,&y,&z);
        d[x]+=z;
        d[y+1]-=z;
    }
    
    //求解f{i]数组 和 sum[i]数组   
    for(int i=1;i<=n;i++){
        f[i]=f[i-1]+d[i];
        sum[i]=sum[i-1]+f[i];
    }
    
    //q次询问 输出sum[x,y]区间和 
    for(int i=1;i<=q;i++)
    {
        scanf("%d %d",&x,&y);
        printf("%d
",sum[y]-sum[x-1]);
    }
}

二维前缀和

#include<bits/stdc++.h>
#define REP(i, a, b) for(register int i = (a); i < (b); i++)
#define _for(i, a, b) for(register int i = (a); i <= (b); i++)
using namespace std;

const int N = 100;
int a[N][N], n;

int main(){
    scanf("%d", &n);
    _for(i, 1, n)
        _for(j, 1, n){
            int x; scanf("%d", &x);
            a[i][j] = x + a[i-1][j] + a[i][j-1] - a[i-1][j-1];
        }
    
    int x1, y1, x2, y2;
    while(~scanf("%d%d%d%d", &x1, &y1, &x2, &y2))
        printf("%d
",a[x2][y2]-a[x1-1][y2]- a[x2][y1-1] + a[x1-1][y1-1]);
    return 0;
}

二维差分

const int N = 100;
int a[N][N], n, m;
int main(){
    scanf("%d%d", &n, &m);
    _for(i, 1, m){
        int x1, y1, x2, y2, p;
        scanf("%d%d%d%d%d", &x1, &y1, &x2, &y2, &p);
        a[x1][y1] += p; a[x2+1][y2+1] += p;
        a[x2+1][y1] -= p; a[x1][y2+1] -= p;
    } 
    _for(i, 1, n)
        _for(j, 1, n)
            a[i][j] += a[i-1][j] + a[i][j-1] - a[i-1][j-1];     
    Print a[i][j] //输出a[i][j]   
}

树状数组

Cf#609D：

ll sum1[2e5+5],sum2[maxn],a[maxn],pos[maxn];
int n;
ll lowbit(ll x){return x & -x;} 
void add(ll *sum,ll x,ll v){
    while(x <= n){
        sum[x] += v;
        x += lowbit(x);
    }
}
ll query(ll *sum,ll x){
    ll res = 0;
    while(x > 0){
        res += sum[x];
        x -= lowbit(x);
    }
    return res;
} 
int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a[i];
        pos[a[i]] = i;//值为a[i]的元素 "位置"在为i的地方 
    }
    ll ans1 = 0;
    for(int i=1;i<=n;i++){
        ans1 += i - 1 - query(sum1,pos[i]); //求逆序数 和相加 
        add(sum1,pos[i],1); //前i个位置中已经出现了的比当前数小的数的个数+1 
        add(sum2,pos[i],pos[i]); //比第i个位置小的 位置+pos[i] 
        int mid,l = 1,r = n;
        while(l<=r){ //二分需要靠拢的最中间的位置 
            mid = (l+r)>>1;
            if(query(sum1,mid)*2 <= i) l = mid+1;
            else r = mid - 1;
        }
        ll ans2 = 0,cnt = query(sum1,mid),sum = query(sum2,mid);
        ans2 += mid*cnt-sum-cnt*(cnt-1)/2;
        cnt = i-cnt,sum = query(sum2,n) - sum;
        ans2 += sum-cnt*(mid+1)-cnt*(cnt-1)/2;
        cout<<ans1+ans2<<" ";
    }
} 

树状数组板子

int lowbit(int x) {return x & -x;}

void add(int x, int k) {
  while (x <= n) {  //不能越界
    c[x] = c[x] + k;
    x = x + lowbit(x);
  }
}
int getsum(int x) {  // a[1]……a[x]的和
  int ans = 0;
  while (x >= 1) {
    ans = ans + c[x];
    x = x - lowbit(x);
  }
  return ans;
}

树状数组区间加 & 区间求和

int t1[MAXN], t2[MAXN], n;
inline int lowbit(int x) { return x & (-x); }
void add(int k, int v) {
  int v1 = k * v;
  while (k <= n) {
    t1[k] += v, t2[k] += v1;
    k += lowbit(k);
  }
}
int getsum(int *t, int k) {
  int ret = 0;
  while (k) {
    ret += t[k];
    k -= lowbit(k);
  }
  return ret;
}
void add1(int l, int r, int v) {
  add(l, v), add(r + 1, -v);  //将区间加差分为两个前缀加
}
long long getsum1(int l, int r) {
  return (r + 1ll) * getsum(t1, r) - 1ll * l * getsum(t1, l - 1) - (getsum(t2, r) - getsum(t2, l - 1));
}

线段树

线段树例题线段树单点更新区间求和HPU：

const int maxn=1000000+10;
const int INF=0x3f3f3f3f;
int a[maxn],k[maxn],N;
ll pre[maxn],nxt[maxn];
struct Tree{//
    ll x[maxn];
    void init(int x){//初始化 
        N=1;
        while(N<=x*2) N*=2;
    }
    void update(int k,int q){//单点更新 
        k+=N-1;
        x[k]=q;
        while(k){
            k=(k-1)/2;
            x[k]=min(x[k*2+1],x[k*2+2]);
        }
    }
    ll query(int a,int b,int l,int r,int k){//区间查询 
        if(r<a || b<l) return INF; //处理边界 
        if(a<=l && r<=b) return x[k]; //处理边界 
        else{
            ll vl=query(a,b,l,(l+r)/2,k*2+1);
            ll vr=query(a,b,(l+r)/2+1,r,k*2+2);
            return min(vl,vr);
        }
    }
}tp,tn;
int main(){
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%d",&k[i]);
    tp.init(n);
    ll sum=0; 
    for(int i=1;i<=n;i++){//前缀和 建线段树
        scanf("%d",&a[i]);
        sum+=a[i];
        tp.update(i,sum);
    }
    sum=0;
    for(int i=n;i>=1;i--){ //后缀和 建线段树 
        sum+=a[i]; tn.update(i,sum);}
    //i从1~n  sum为数组总和     定义的最大区间值 就=sum-最小前缀-最小后缀
    ll ans=0;
    for(int i=1;i<=n;i++){
        ans+=sum;
        ans-=tp.query(max(i-k[i]-1,0),max(i-1,0),0,N-1,0);
        ans-=tn.query(min(i+1,n+1),min(i+k[i]+1,n+1),0,N-1,0);
    }
    printf("%lld
",ans);
    return 0;
}

线段树区间更新，区间查询，维护赋值修改

void up(int p){
    if (!p) return;
    s[p] = s[p * 2] + s[p * 2 + 1];
}

void down(int p, int l, int r){
    if (col[p]) {
        int mid = (l + r) / 2;
        s[p * 2] = col[p] * (mid - l + 1);
        s[p * 2 + 1] = col[p] * (r - mid);
        col[p * 2] = col[p * 2 + 1] = col[p];
        col[p] = 0;
    }
}

void modify(int p, int l, int r, int x, int y, int c){
    if (x <= l && r <= y){
        s[p] = (r - l + 1) * c;  //仅修改该结点
        col[p] = c;  //增加标记，子结点待修改
        return;
    }
    down(p, l, r);  //下传lazy标记
      int mid = (l + r) / 2;
    if (x <= mid) modify(p * 2, l, mid, x, y, c);
    if (y > mid) modify(p * 2 + 1, mid + 1, r, x, y, c);
    up(p);
}

线段树单点更新区间查询，维护最小值

#include <iostream>
using namespace std;
const int inf = 0x3f3f3f3f;
const int maxn = 110;
int a[maxn];//原数组 
int minv[4 * maxn];//维护最小值

/*
单点更新
区间查询 
*/ 

//维护区间最小值
void pushup(int id) {
    minv[id] = min(minv[id << 1], minv[id << 1 | 1]);
}

//建树 
void build(int id, int l, int r) {
    if (l == r) {
        minv[id] = a[l];
        return;
    }
    int mid = (l + r) >> 1;
    build(id << 1, l, mid);
    build(id << 1 | 1, mid + 1, r);
    pushup(id);
}
//更新 
void update(int id, int l, int r, int x, int v) {
    if (l == r) {
        minv[id] = v;
        return;
    }
    int mid = (l + r) >> 1;
    if (x <= mid) {
        update(id << 1, l, mid, x, v);
    } else {
        update(id << 1 | 1, mid + 1, r, x, v);
    }
    pushup(id);
}
//查询 
int query(int id,int l,int r,int x,int y){
    if(x <= l && r <= y){
        return minv[id];
    }
    int mid = (l + r) >> 1;
    int ans = inf;
    if( x <= mid){
        ans = min(ans,query(id << 1, l, mid, x,y));
    }
    if( y > mid){
        ans = min(ans,query( id<< 1 | 1,mid + 1,r,x,y));
    }
    return ans;
}
int main() {
    int n;
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        cin >> a[i];
    }
    build(1, 1, n);
    int q;
    cin >> q;
    for (int i = 0; i < q; ++i) {
        int x, v;
        cin >> x >> v;
        update(1, 1, n, x, v);
    }
    int p;
    cin >> p;
    for (int i = 0; i < p; ++i) {
        int l, r;
        cin >> l >> r;
        cout << query(1, 1, n, l, r) << endl;
    }
    return 0;
}

数论

费马小定理降幂

KMP

KMP模板题:在S中找P第一次出现的位置

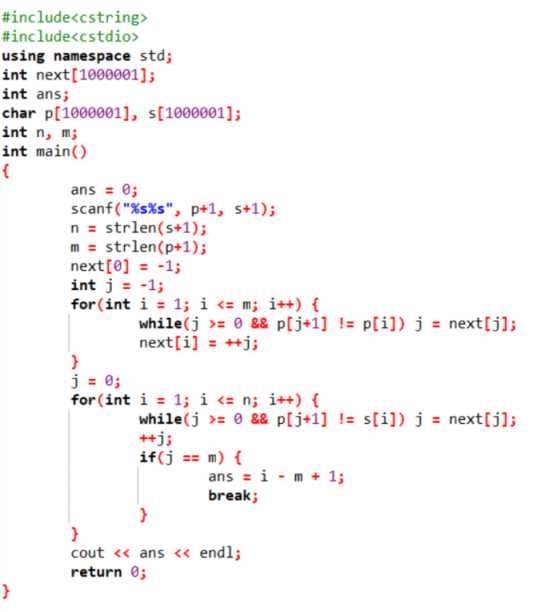
KMP模板题：求出P在S中出现了多少次，可以部分重叠

KMP模板题：求出P在S中出现了多少次，不可以部分重叠

KMP变形题1：

求出字符串A最少重复几次才能使得B是A的子串。
思路：先将A重复若干次，得到一个足够长的字符串S。S 最长 = A.len+B.len；用KMP成功匹配的第一次位置，计算最少次数。如果kmp匹配不成功就不满足。

KMP变形题2：

给定两个字符串P和S，找一个最长的字符串T，满足T是P的前缀，也是S的后缀。
思路：如果你对KMP的过程非常清楚的话，你会发现KMP用P去匹配S的过程中，如果S[i]匹配上了P[j]那就说明P[1..j]是S[1..i]的最长后缀，同时P[1..j]显然是P的前缀。所以我们只要找到最后一个匹配上S[n]的P[j]的即可，这时j就是答案。

if(++j == m){
    if(j == n) break;
    j = nxt[j];
}

LCA

LCA例题树上倍增求两点距离

#include<cstdio>
#include<algorithm>
using namespace std;
struct edge{
    int v,next,val;
}e[100005];
int n,m,heads[50005],q[50005],head,tail,fa[17][50005],dis[50005],dep[50005],cnt;
void add(int u,int v,int val){
    e[++cnt].next=heads[u];
    heads[u]=cnt;
    e[cnt].v=v;
    e[cnt].val=val;
}
int dfs(int u){
    for(int i=heads[u];i;i=e[i].next) {
        if(e[i].v!=fa[0][u]) {
            dep[e[i].v]=dep[u]+1;
            fa[0][e[i].v]=u;
            dis[e[i].v]=dis[u]+e[i].val;
            dfs(e[i].v);
        }
    }
}
int LCA(int u,int v){
    if(dep[u]>dep[v])swap(u,v);
    for(int i=16;~i;i--)
        if(dep[fa[i][v]]>=dep[u])
            v=fa[i][v];
    if(u==v)return u;
    for(int i=16;~i;i--)
        if(fa[i][u]!=fa[i][v])
        {
            u=fa[i][u];
            v=fa[i][v];
        }
    return fa[0][u];
}
int main(){
    scanf("%d",&n);
    for(int i=1;i<n;i++) {
        int x,y,z;
        x++;y++;
        scanf("%d%d%d",&x,&y,&z);
        add(x,y,z);
        add(y,x,z);
    }
    dep[1]=fa[0][1]=1;
    dfs(1);
    for(int i=1;i<=16;i++)
        for(int j=1;j<=n;j++)
            fa[i][j]=fa[i-1][fa[i-1][j]];
    scanf("%d",&m);
    while(m--){
        int x,y;
        x++;y++;
        scanf("%d%d",&x,&y);
        printf("%d
",dis[x]+dis[y]-2*dis[LCA(x,y)]);
    }
    return 0;
}

LCA性质

LCA例题：HPU-C:XOR PATH

#include<bits/stdc++.h>
using namespace std;
思路：DFS计算从根节点到每个节点的异或和,同时计算倍增。然后利用倍增可以实现O(logn)的查询。小结：学会了树链异或的lca优化方法、还需要熟悉和理解lca原理 
const int N = 1e6+100;
vector<int> G[N];
int pre[N],a[N],par[N];
long long bit[30];
int f[N][30];
int depth[N];

//初始化 
void init(){
    bit[0]=1;
    for(int i=1;i<=29;i++) bit[i]=(bit[i-1]<<1);
}
//倍增
void dfs(int u,int par){
    depth[u]=depth[par]+1;
    f[u][0]=par;
    for(int i=1;bit[i]<=depth[u];i++) f[u][i]=f[f[u][i-1]][i-1];
    for(int v:G[u]){
        if(v!=par) dfs(v,u);
    }
}
//lca
int lca(int x,int y){
    if(depth[x]<depth[y]) swap(x,y);
    for(int i=29;i>=0;i--){
        if(depth[x]-depth[y]>=bit[i]){
            x=f[x][i];
        }
    }
    if(x==y) return x;
    for(int i=29;i>=0;i--){
        if(depth[x]>=(1<<i)&&f[x][i]!=f[y][i]){
            x=f[x][i];
            y=f[y][i];
        }
    }
    return f[x][0];
}
//从根节点1出发 求每个点到根节点的路径异或和 
void DFS1(int u,int fa){
    par[u]=fa;
    pre[u]=pre[fa]^a[u];
    for(int v:G[u]){
        if(v==fa) continue;
        DFS1(v,u);
    }
}

int main(){
    int n,u,v,q;
    cin>>n;
    init();
    //建图 邻接表 
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=0;i<=n;i++) G[i].clear();
    for(int i=1;i<=n-1;i++){
        cin>>u>>v;
        G[u].push_back(v);
        G[v].push_back(u);
    }
    //lca
    dfs(1,0);
    //计算从根节点到每个结点的异或和 
    DFS1(1,0);
    int x,y;
    cin>>q;
    while(q--){
        cin>>x>>y;
        int c=lca(x,y); //lca求出最近公共祖先 
        int f=par[c]; //求出最近公共祖先的父节点  这里再求一次父节点的原因是: 消除祖先的父节点到根节点这段路径(异或了2次)的异或 
        cout<<(pre[x]^pre[f]^pre[c]^pre[y])<<endl; //画图理解:树链上异或两次就等于没有异或  
    }
    return 0;
}