SVD分解
Posted jasonpeng1
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了SVD分解相关的知识,希望对你有一定的参考价值。
奇异值分解(Singular Value Decomposition,SVD)是一种重要的矩阵分解(Matrix Decomposition)方法,可以看做对称方正在任意矩阵上的一种推广,该方法在机器学习的中占有重要地位。
首先讲解一下SVD的理论,然后用python实现SVD,并应用于图像压缩。
---------------------
作者:夕阳下江堤上的男孩
来源:CSDN
原文:https://blog.csdn.net/ye1215172385/article/details/79414702
版权声明:本文为博主原创文章,转载请附上博文链接!
1、奇异值分解(SVD):
设有 A是一个m×n 的实矩阵,则存在一个分解使得:
U 和 V 都是正交矩阵 ,即:
Σ 是一个非负实对角矩阵,U 和 V 的列分别叫做 A 的 左奇异向量和 右奇异向量,Σ 的对角线上的值叫做 A 的奇异值。关于这三个矩阵的求解,如下:
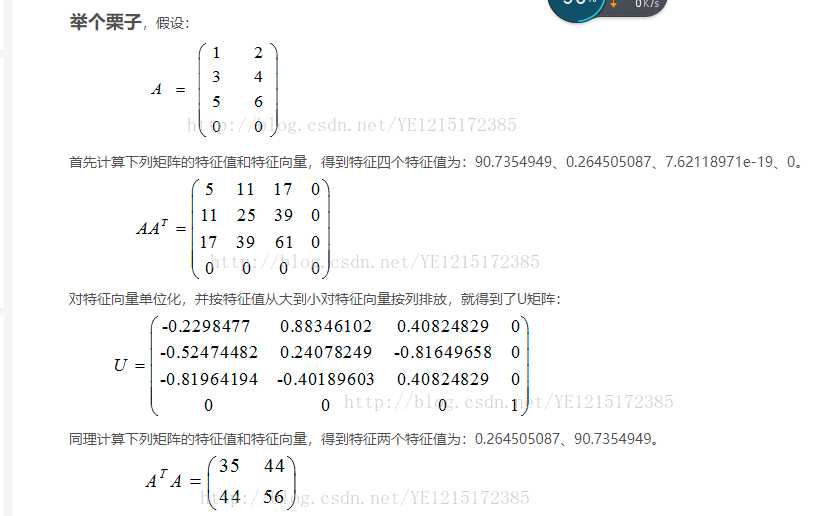
1)、U 的列由 AAT 的特征向量构成,且特征向量为单位列向量
2)、V 的列由 ATA 的特征向量构成,且特征向量为单位列向量
3)、Σ 的对角元素来源于 AAT 或 ATA 的特征值的平方根,并且是按从大到小的顺序排列的。值越大可以理解为越重要。
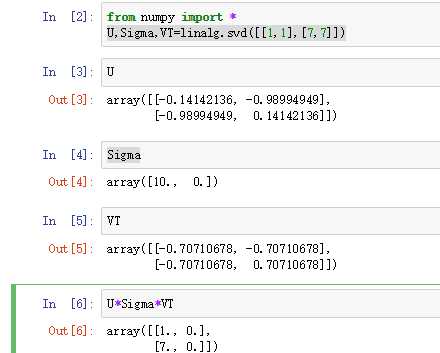
https://www.cnblogs.com/yuzhuwei/p/4126139.html
这里的矩阵相乘我怀疑是出错了。应该是这样使用矩阵相乘
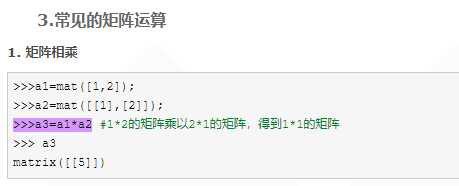
https://www.cnblogs.com/chamie/p/4870078.html
奇异值分解(Singular Value Decomposition,以下简称SVD)是在机器学习领域广泛应用的算法,它不光可以用于降维算法中的特征分解,还可以用于推荐系统,以及自然语言处理等领域。是很多机器学习算法的基石。本文就对SVD的原理做一个总结,并讨论在在PCA降维算法中是如何运用运用SVD的。
1. 回顾特征值和特征向量
我们首先回顾下特征值和特征向量的定义如下:
其中A是一个n×nn×n的矩阵,xx是一个nn维向量,则我们说λλ是矩阵A的一个特征值,而xx是矩阵A的特征值λλ所对应的特征向量。
求出特征值和特征向量有什么好处呢? 就是我们可以将矩阵A特征分解。如果我们求出了矩阵A的nn个特征值λ1≤λ2≤...≤λnλ1≤λ2≤...≤λn,以及这nn个特征值所对应的特征向量{w1,w2,...wn}{w1,w2,...wn},,如果这nn个特征向量线性无关,那么矩阵A就可以用下式的特征分解表示:
其中W是这nn个特征向量所张成的n×nn×n维矩阵,而ΣΣ为这n个特征值为主对角线的n×nn×n维矩阵。
一般我们会把W的这nn个特征向量标准化,即满足||wi||2=1||wi||2=1, 或者说wTiwi=1wiTwi=1,此时W的nn个特征向量为标准正交基,满足WTW=IWTW=I,即WT=W−1WT=W−1, 也就是说W为酉矩阵。
这样我们的特征分解表达式可以写成
注意到要进行特征分解,矩阵A必须为方阵。那么如果A不是方阵,即行和列不相同时,我们还可以对矩阵进行分解吗?答案是可以,此时我们的SVD登场了。

特征值和奇异值的关系:奇异值就是矩阵Data*Data.T特征值的平方根——《机器学习实战》
在科学和工程中,一直存在这样一个普遍事实:在某个奇异值的数目(r个)之后,其他的奇异值都置为0。这就意味着数据集中仅有r个重要特征,而其余特征则都是噪声或冗余特征。
SVD 和PCA 的关系:
现在来看一下SVD和PCA的关系。
我们讲到要用PCA降维,需要找到样本协方差矩阵X˜TX˜X~TX~的最大的k个特征向量,然后用这最大的k个特征向量张成的矩阵来做低维投影降维。
注意,SVD也可以得到协方差矩阵X˜TX˜X~TX~最大的k个特征向量张成的矩阵。
但是SVD有个好处,有一些SVD的实现算法可以不求先求出协方差矩阵,也能求出右奇异矩阵VV。也就是说,PCA算法可以不用做特征分解,而是做SVD来完成。这也是为什么很多工具包中PCA算法的背后真正的实现是用的SVD,而不是我们认为的暴力特征分解。
另一方面,注意到PCA仅仅使用了我们SVD的右奇异矩阵,没有使用左奇异矩阵。而左奇异矩阵可以用于行数的压缩,右奇异矩阵可以用于列数,也就是PCA降维。
所以,有了SVD就可以得到两个方向的PCA。
---------------------
作者:Hanna216
来源:CSDN
原文:https://blog.csdn.net/qq_24464989/article/details/79834564
版权声明:本文为博主原创文章,转载请附上博文链接!
https://blog.csdn.net/qq_24464989/article/details/79834564
重构原始矩阵:——《机器学习实战》
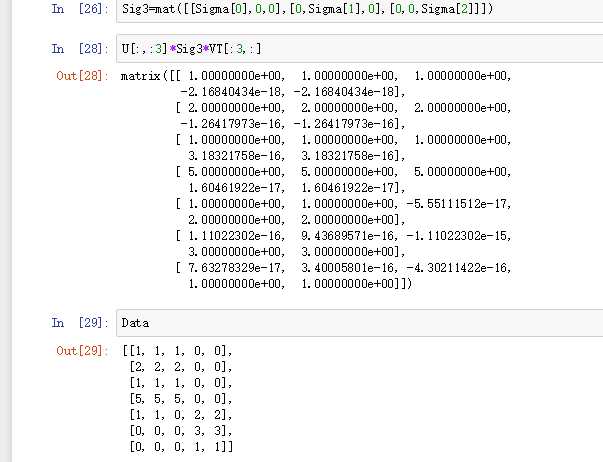
如何确定需要保留的奇异值个数?
我们是如何知道仅需保留前3个奇异值的呢?确定要保留的奇异值的数目有很多启发式的策略,其中一个典型的做法就是保留矩阵中90%的能量信息。为了计算总能量信息,我们将所有的奇异值求其平方和。于是可以将奇异值的平方和累加到总值的90%为止。另一个启发式策略就是,当矩阵上有上万的奇异值时,那么就保留前面的2000或3000个。
以上是关于SVD分解的主要内容,如果未能解决你的问题,请参考以下文章