梯度下降算法分类总结
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了梯度下降算法分类总结相关的知识,希望对你有一定的参考价值。
引言
梯度下降法 (Gradient Descent Algorithm,GD) 是为目标函数J(θ),如代价函数(cost function), 求解全局最小值(Global Minimum)的一种迭代算法。
为什么使用梯度下降法
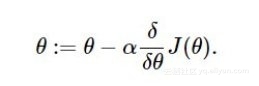
α表示学习速率(learning rate)。
梯度下降法的工作原理
梯度下降法的类型
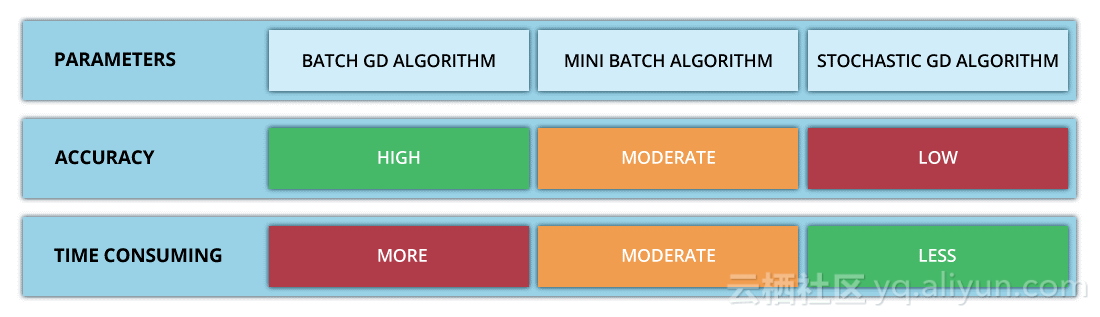
基于如何使用数据计算代价函数的导数,梯度下降法可以被定义为不同的形式(various variants)。确切地说,根据使用数据量的大小(the amount of data),时间复杂度(time complexity)和算法的准确率(accuracy of the algorithm),梯度下降法可分为:
1. 批量梯度下降法(Batch Gradient Descent, BGD);
2. 随机梯度下降法(Stochastic Gradient Descent, SGD);
3. 小批量梯度下降法(Mini-Batch Gradient Descent, MBGD)。
批量梯度下降法原理
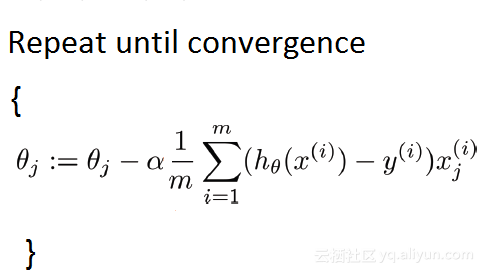
其中,m是训练样本(training examples)的数量。
Note:
1. 如果训练集有3亿条数据,你需要从硬盘读取全部数据到内存中;
2. 每次一次计算完求和后,就进行参数更新;
3. 然后重复上面每一步;
4. 这意味着需要较长的时间才能收敛;
5. 特别是因为磁盘输入/输出(disk I/O)是系统典型瓶颈,所以这种方法会不可避免地需要大量的读取。
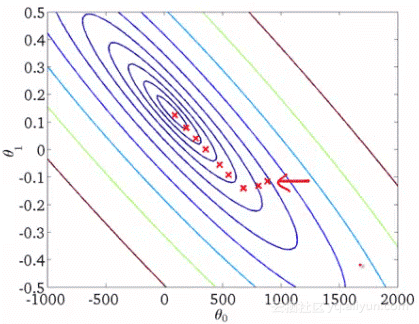
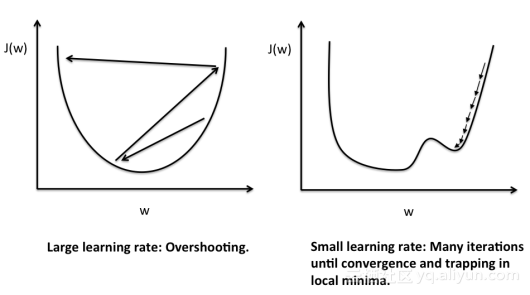
上图是每次迭代后的等高线图,每个不同颜色的线表示代价函数不同的值。运用梯度下降会快速收敛到圆心,即唯一的一个全局最小值。批量梯度下降法不适合大数据集。
随机梯度下降法原理

这里m表示训练样本的数量。
如下为随机梯度下降法的伪码:
1. 进入内循环(inner loop);
2. 第一步:挑选第一个训练样本并更新参数,然后使用第二个实例;
3. 第二步:选第二个训练样本,继续更新参数;
4. 然后进行第三步…直到第n步;
5. 直到达到全局最小值
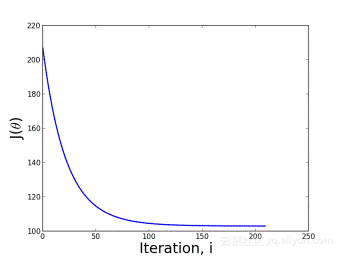
如下图所示,随机梯度下降法不像批量梯度下降法那样收敛,而是游走到接近全局最小值的区域终止。
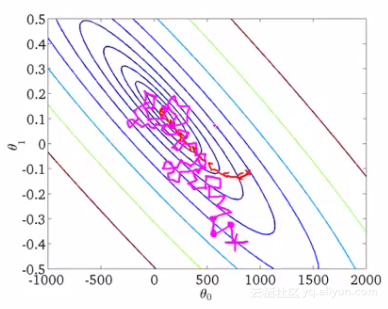
小批量梯度下降法原理
小批量梯度下降法是最广泛使用的一种算法,该算法每次使用m个训练样本(称之为一批)进行训练,能够更快得出准确的答案。小批量梯度下降法不是使用完整数据集,在每次迭代中仅使用m个训练样本去计算代价函数的梯度。一般小批量梯度下降法所选取的样本数量在50到256个之间,视具体应用而定。
1.这种方法减少了参数更新时的变化,能够更加稳定地收敛。
2.同时,也能利用高度优化的矩阵,进行高效的梯度计算。
随机初始化参数后,按如下伪码计算代价函数的梯度: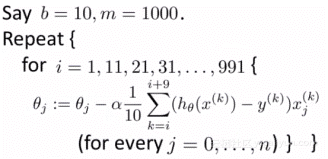
以上是关于梯度下降算法分类总结的主要内容,如果未能解决你的问题,请参考以下文章