[HDOJ 1003]动态规划法求和最大的连续子序列

Posted 2021-03-19 zhouyijoe

题目地址: http://acm.hdu.edu.cn/showproblem.php?pid=1003

Problem Description

Given a sequence a[1],a[2],a[3]......a[n], your job is to calculate the max sum of a sub-sequence. For example, given (6,-1,5,4,-7), the max sum in this sequence is 6 + (-1) + 5 + 4 = 14.

 

Input

The first line of the input contains an integer T(1<=T<=20) which means the number of test cases. Then T lines follow, each line starts with a number N(1<=N<=100000), then N integers followed(all the integers are between -1000 and 1000).

 

Output

For each test case, you should output two lines. The first line is "Case #:", # means the number of the test case. The second line contains three integers, the Max Sum in the sequence, the start position of the sub-sequence, the end position of the sub-sequence. If there are more than one result, output the first one. Output a blank line between two cases.

 

Sample Input

2

5 6 -1 5 4 -7

7 0 6 -1 1 -6 7 -5

 

Sample Output

Case 1:

14 1 4

 

Case 2:

7 1 6

 

题目的大致意思就是要你从给定的数组中找出一段连续的子序列，使得这段连续的子序列中所有数字的总和不小于数组中其他任何一段连续子序列中数字的总和。只有傻子(我QAQ)才会用暴力枚举的方法来做这题，必TLE。用分治法来做也是一种思路，不过我没试过，不知道会不会TLE。最好的方法就是动态规划。那么怎么做呢？

 

动态规划法其实在某种程度上也用的是枚举的思路，只不过枚举的方法比较巧妙而已。显然，不论是哪一段连续子序列都是有终点的(废话)，我们可以依次把数组中每一个元素都看作是连续子序列的终点，把以该元素为终点的所有连续子序列找出来。这样就可以枚举出数组中所有的连续子序列。

 

例如，有一个数组，它所包含的元素依次是5,9,2,4。以第一个元素为终点的连续子序列有"5"，以第二个元素为终点的连续子序列有"5,9","9"，以第三个元素为终点的连续子序列有"5,9,2","9,2","2"，以第四个元素为终点的连续子序列有"5,9,2,4","9,2,4","2,4","4"。于是以上找到的所有的连续子序列即为该数组中的所有连续子序列。

 

“讲了半天，你这不还是暴力枚举嘛......" 我们当然不是要以这种方式来暴力枚举，而是要通过这样一种思路，找到其中的递推关系。既然现在我们是通过终点来寻找连续子序列的话，那么就定义一个函数dp(i):以数组中第i个元素作为终点，找出所有以第i个元素为终点的连续子序列，并依次求出这些连续子序列中所有元素的总和，所有总和中的最大值即为dp(i)的值。

 

例如，一个数组中的元素有1,-2,4,3。以第3个元素，也就是4，作为终点，找出所有以它为终点的连续子序列:"1,-2,4","-2,4","4"。序列"1,-2,4"的所有元素总和为3，序列"-2,4"的所有元素总和为2，序列"4”的所有元素总和为4。而4>3>2，则4为所有总和中的最大值，于是dp(3)=4。

 

相信你已经明白了这里定义的函数dp(i)的含义了。那么如何找到这个函数的递推关系呢？

 

说到递推关系，首先当然要明确递推的起点。显然dp(1)的值就是数组中的第一个元素，这就是递推的起点。接下来就只需要找到dp(i - 1)与dp(i)之间的关系，我们就可以求出dp(1),dp(2), ...... ,dp(i), ...... ,dp(n)了。很容易就可以知道，当dp(i - 1) >= 0时,dp(i) = dp(i - 1) + arr[i](arr[i]表示数组中第i个元素);当dp(i - 1) < 0时,dp(i) = arr[i]。

 

不过求出这些dp的值有什么用呢？刚才讲过，依次以数组中每个元素为终点，找出以这些元素为终点的所有连续子序列，就能够枚举出数组的所有连续子序列。而求出所有dp值的过程其实就相当于把所有连续子序列都枚举了一遍。既然已经找出了所有"局部"的最大值，那我们把这些"局部"的最大值合起来，找到"全局"的最大值，不就得到了问题的最终答案了嘛？所以，接下来我们要做的，就是从所有的dp值中，找出最大的那一个dp值，这个最大的dp值，就是元素总和最大的连续子序列。

 

终于把最关键的讲完了，接下来放出代码~这里先暂时只考虑求最大和的问题，所以只演示一个用来求最大和的函数，其他的后面再说。代码可能写得比较啰嗦，不过这是为了让大家容易看得明白。

 1 #include <cstdio>
 2 #include <climits>
 3 #include <algorithm>
 4 using namespace std;
 5 
 6 int getMaxSum(int* arr,int high)
 7 {
 8     const int SIZE = 1e4;
 9     int dp[SIZE] = {0};
10 
11     for(int i = 0;i <= high;++i)
12     {
13         if(i == 0)
14         {
15             dp[i] = arr[i];
16         }
17         else if(i > 0)
18         {
19             dp[i] = max(dp[i - 1] + arr[i],arr[i]);
20         }
21     }
22 
23     int maxSum = INT_MIN;
24     for(int i = 0;i <= high;++i)
25     {
26         if(dp[i] > maxSum)
27         {
28             maxSum = dp[i];
29         }
30     }
31 
32     return maxSum;
33 }

 

现在我们已经解决了如何求最大和的问题了，不过这道oj题还要求我们给出所求连续子序列的起点位置和终点位置。如果是用暴力枚举法的话，很容易就可以记录下起点位置和终点位置。不过如果是用动态规划法的话，想要记录下位置，可能还得稍微动一下脑子。不过也不难。我们自己手动模拟一下求dp值的过程，就可以找到其中的规律了。

下图是计算一个数组的所有dp值的过程。

 

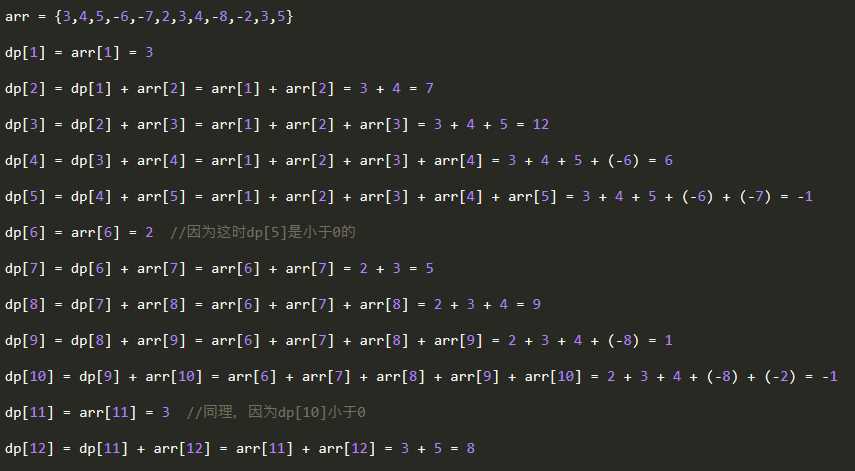
仔细观察上图，就可以找到其中的规律:计算一个数组的所有dp值的过程，其实是一个"从头加到尾"的过程，只不过在dp值小于零的地方需要"断开"。具体地说，计算一个数组的所有dp值时，我们需要做的是从第一个元素开始，依次取数，把这些数一个一个加起来。如果当加到第i个数时所得到的和为一个负数，则把前面i个数的和直接"丢掉"不要，然后从第i + 1个数开始，再从零开始加，之后循环往复地重复上述步骤。于是，我们就可以以这样一种方法得到每个dp值对应的连续子序列的起点位置和终点位置:一开始把起点位置设为1，也就是整个数组的起点。显然，dp(1)的终点位置也是1。然后求后面的dp值时，只要dp(i - 1)的值是非负的，那么dp(i)对应的起点位置就是dp(i - 1)的起点位置，而终点位置就是dp(i - 1)的终点位置 + 1。如果dp(i - 1)的值是负数，则dp(i)对应的起点位置就应该是i，终点位置也是i。

 

也许会有人觉得需要另外开两个数组，保存每个dp值对应的起点位置和终点。但其实没必要。我们只需要在每求出一个dp值时，都去更新一下最大值和起点终点位置即可。具体的做法见下面的代码。

 

 1 #include <cstdio>
 2 #include <climits>
 3 
 4 const int SIZE = 1e5 + 10;
 5 int arr[SIZE];
 6 int dp[SIZE];
 7 
 8 int main()
 9 {
10     int nCase = 0;
11     scanf("%d",&nCase);
12 
13     for(int i = 1;i <= nCase;++i)
14     {
15         int n = 0;
16         scanf("%d",&n);
17         for(int j = 0;j < n;++j)
18         {
19             scanf("%d",&arr[j]);
20         }
21 
22         int maxSum = INT_MIN;
23         int mLow = 0;  //和最大的连续子序列的下界
24         int mHigh = 0;  //和最大的连续子序列的上界
25         int tLow = 0;  //以第j个元素为结尾的和最大的连续子序列的下界
26         int tHigh = 0;  //以第j个元素为结尾的和最大的连续子序列的上界
27         for(int j = 0;j < n;++j)
28         {
29             if(j == 0)
30             {
31                 dp[j] = arr[j];
32                 tLow = j;
33                 tHigh = j;
34             }
35             else if(j > 0)
36             {
37                 if(dp[j - 1] >= 0)
38                 {
39                     dp[j] = dp[j - 1] + arr[j];
40                     tHigh = j;
41                 }
42                 else if(dp[j - 1] < 0)
43                 {
44                     dp[j] = arr[j];
45                     tLow = j;
46                     tHigh = j;
47                 }
48             }
49 
50             if(dp[j] > maxSum)
51             {
52                 maxSum = dp[j];
53                 mLow = tLow;
54                 mHigh = tHigh;
55             }
56         }
57 
58         if(i == nCase)
59         {
60             printf("Case %d:
%d %d %d
",i,maxSum,mLow + 1,mHigh + 1);
61         }
62         else
63         {
64             printf("Case %d:
%d %d %d

",i,maxSum,mLow + 1,mHigh + 1);
65         }
66     }
67 }

 

上面的代码就已经足够让这道oj题AC了。不过，其实上面的做法还不是最好的做法。我们其实没有必要开一个数组保存dp值。就像上面说过的，求dp值的过程其实就是"从头加到尾"的过程。我们只需要弄一个变量sum，从数组的第一个元素开始，一个一个取数加到sum中，每加一个数后都用sum去更新一下最大值。一旦sum的值为负数，就把sum重新置零，也就是把前面得到的总和"丢掉"不要，然后再从下一个数开始一个一个取数加到sum中......不断地重复这样的步骤即可。

 

下面的代码就是一种比较好的做法。

 

#include <cstdio>
#include <climits>

int main()
{
    int nCase = 0;
    scanf("%d",&nCase);

    for(int i = 1;i <= nCase;++i)
    {
        int n = 0;
        scanf("%d",&n);

        int high = 0;
        int low = 0;
        int lowTemp = 1;
        int maxSum = INT_MIN;
        int sum = 0;
        int ele = 0;
        for(int j = 1;j <= n;++j)
        {
            scanf("%d",&ele);
            sum += ele;
            if(sum > maxSum)
            {
                maxSum = sum;
                low = lowTemp;
                high = j;
            }
            if(sum < 0)
            {
                sum = 0;
                lowTemp = j + 1;
            }
        }

        if(i == nCase)
        {
            printf("Case %d:
%d %d %d
",i,maxSum,low,high);
        }
        else
        {
            printf("Case %d:
%d %d %d

",i,maxSum,low,high);
        }
    }
}

 

(完)