初探莫队

Posted 2021-03-18 lcez56jsy

2019年的某月某天某神仙讲了莫队，但是我一直咕咕咕到了2020年

什么是莫队

莫队是一种优雅的暴力，也是用来完成区间询问的。普通莫队复杂度(O(n sqrt n))。一种十分优美的离线做法

前置芝士

0.拥有脑子

1.(STL)中(sort)的(cmp)

2.看/写超长的三目运算符的耐心

3.分块的思想

当然了如果不会这些也没有关系，下面还会再讲的

正片开始

先来一道卡了莫队的莫队模板题
HH的项链


最最暴力的做法：显然我们可以对每个询问暴力跑一次，但显然(O(n^2))跑不起。
在上面的暴力中，我们浪费了大量之前遍历过的区间的信息，现在考虑利用起这些信息。我们可以设置两个指针(l,r)表示当前所处的区间左端点和右端点。初始化(l=1,r=0)。（为了避免某些神奇的(RE)）如果(l,r)不与询问区间的端点重合，就不断的跳(l,r)来更新答案。如果(l)在左端点右边，就不断向左跳，同时将(l)跳到的数统计进答案中，直到与左端点重合。如果(l)在左端点左边，就不断往右跳，同时将曾经待过的点从答案中删掉。对于这个题来说，可以用(cnt[x])表示(x)这个数出现的次数，如果某次增加时，(cnt[x]==0),(ans)就(+1),如果某次删除时发现删完后(cnt[x]==0),(ans)就(-1)。

我们发现上面这个优化对于这种图来说效率极高：

其中(x_i)表示第(i)次询问对应的区间

但是对于这种数据来说就凉了

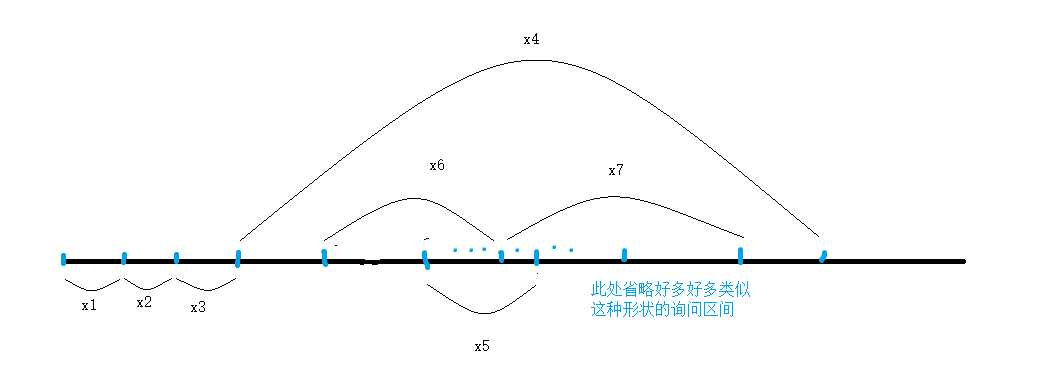
上面的优化方式在(x_4)里面不断得左右来回跳，导致浪费了大量的时间。

所以我们不妨把询问的区间进行排序。这样做就必须离线了。怎么排序呢？按照左端点单调递增？显然右端点无序会让这个优化只增加(O(nlogn))的排序复杂度。这时候，就要用到分块思想了。

我们把整个序列分成(sqrt n)个块，按照(l)所在的块升序排列为第一关键字，(r)升序排列为第二关键字排序。感觉好像没有什么用诶？但确实是个极大的优化至于为什么我也不知道

代码如下：

struct Q{
   int l,r,id,nub;//nub表示左端点在哪个块里
}qry[200009];
bool cmp(Q a,Q b)
{
    if(a.nub!=b.nub) return a.nub<b.nub;
    return a.r<b.r; 
}

当然卡常一点也可以写成这样：

bool cmp(Q a,Q b)
{ 
   return (a.nub^b.nub)?a.nub<b.nub:a.r<b.r;
}

过莫队板子的必备技能是卡常
这样基本的莫队就撒花完结了。

因为这道板子题卡了莫队，所以请走数据弱化版D_QUERY
板子题代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<vector>
#include<map>
#include<queue>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
inline ll read()
{
    char ch=getchar();
    ll x=0;bool f=0;
    while(ch<'0'||ch>'9')
    {
        if(ch=='-') f=1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        x=(x<<3)+(x<<1)+(ch^48);
        ch=getchar();
    }
    return f?-x:x;
}
int n,q,a[30009],ans[200009],cnt[1000009],all;
struct Q{
    int l,r,nub,id;
}qry[200009];
bool cmp(Q a,Q b)
{
    if(a.nub!=b.nub) return a.nub<b.nub;
    return a.r<b.r; //由于这题不卡常所以就没有卡
}
void add(int k)
{
    if(!cnt[a[k]]) all++;
    cnt[a[k]]++;
}
void del(int k)
{
    cnt[a[k]]--;
    if(!cnt[a[k]]) all--;
}
int main()
{
    n=read();
    for(int i=1;i<=n;i++)
     a[i]=read();
    q=read();
    int sn=sqrt(n);
    for(int i=1;i<=q;i++)
    {
        qry[i].id=i;qry[i].l=read();qry[i].r=read();
        qry[i].nub=qry[i].l/sn+1;
        if(qry[i].l%sn==0) qry[i].nub--;
    }   
    sort(qry+1,qry+1+q,cmp);
    int l=1,r=0;
    for(int i=1;i<=q;i++)
    {
        while(r<qry[i].r) add(++r);
        while(r>qry[i].r) del(r--);
        while(l<qry[i].l) del(l++);
        while(l>qry[i].l) add(--l);
        ans[qry[i].id]=all;
    }  
    for(int i=1;i<=q;i++)
     printf("%d
",ans[i]);
}

莫队的玄学优化

奇偶性排序

虽然上面的排序方法优化很大，但是能不能更快一点以便卡过毒瘤题呢？
方法当然是有的辣。
我们先来康康按照上面的排序方法会排出来个啥

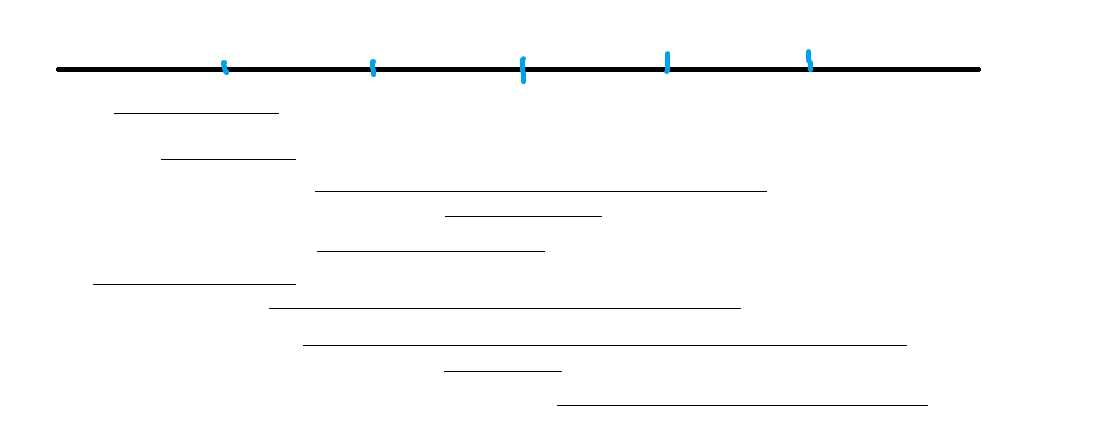
这是一堆询问区间以及并不优美的块的分界线
排序后：

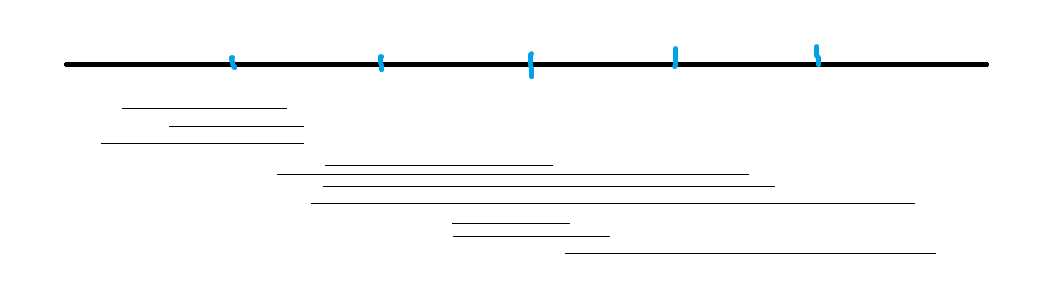
这样左端点跳动幅度不大，右端点在同一个块内也是递增的。但是当(r)从一个块跳到下一个块的时候发现有时候会倒退回来好多，然后又要重新向右跳。是不是有点浪费？所以奇偶性排序就是在奇数块内右端点按升序排序，偶数块内右端点按降序排序，这样右端点在往回跳的时候就能顺带跳完偶数块的询问。理论上能快一半

上面的按照奇偶性排序：

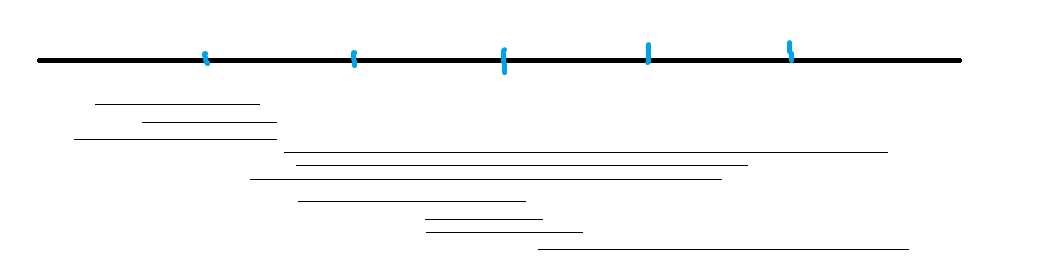
手动模拟(r)的跳跃发现真的优化了不少
代码：

bool cmp(Q a,Q b)
{
  return (a.nub^b.nub)?(a.nub<b.nub):((a.nub%2)?a.r<b.r:a.r>b.r);
}

乱七八糟系列

(pragma GCC optimize(2),pragma GCC optimize (3),register),快读快输，(inline),把(for)里的(i++)换成(++i),用三目运算符代替blabla(待会卡带修莫队板子要用)

带修莫队

现在毒瘤出题人要求修改，怎么办呢？
就像这道题：数颜色


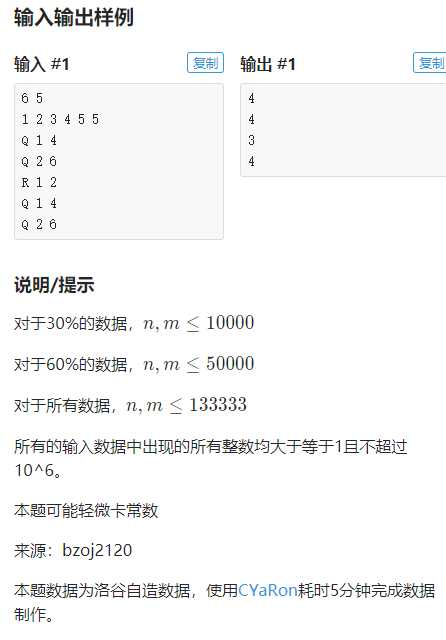
在很久很久以前，这道题是可以拿树套树卡过的你甚至只用去搞搞set，但是现在拿带修莫队都要吸氧了(qaq)

好了我们回到正题。
我们只需要在原来的莫队的基础上再加一维时间轴。将询问和修改分开存储。如果这次询问的时间在当前时间之后，就不断修改，直到时间相同。如果询问时间在当前时间之前，就再改回去，我们可以用(swap)做到，从而不用再开变量维护原来的值。

当然了，排序方式也有变化。这次我们按照(l)所在的块为第一关键字，(r)所在的块为第二关键字，时间为第三关键字进行排序。同时，奇偶性排序也不再适用。
排序：

bool cmp(Q a,Q b)
{
    return (bl[a.l]^bl[b.l])?bl[a.l]<bl[b.l]:((bl[a.r]^bl[b.r])?bl[a.r]<bl[b.r]:a.ti<b.ti);
}

注意块的大小会对复杂度有着极大的影响。据大佬证明当块的大小为(n^{frac{3}{4}})时，复杂度最优。但是我不会证。

由于这个题窝太菜了，不拿(O_2)实在是卡不过去，所以只好放上一份加(O_2)的代码了

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<vector>
#include<map>
#include<queue>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
inline int read()
{
    char ch=getchar();
    int x=0;bool f=0;
    while(ch<'0'||ch>'9')
    {
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        x=(x<<3)+(x<<1)+(ch^48);
        ch=getchar();
    }
    return f?-x:x;
}
int n,k,q,a[133339],bl[133339],ans[133339],cnt[1000009];
int all;
struct Q{
    int l,r,ti,id;
}qry[133339];
struct M{
    int p;
    int col;
}mdi[133339];
bool cmp(Q a,Q b)
{
    return (bl[a.l]^bl[b.l])?bl[a.l]<bl[b.l]:((bl[a.r]^bl[b.r])?bl[a.r]<bl[b.r]:a.ti<b.ti);
}
inline void add(int k)
{
    if(!cnt[a[k]]) all++;
    cnt[a[k]]++;
}
inline void del(int k)
{
    cnt[a[k]]--;
    if(!cnt[a[k]]) all--;
}
inline void modi(int i,int ti)
{
    if(mdi[ti].p>=qry[i].l&&mdi[ti].p<=qry[i].r)
    {
        int x=--cnt[a[mdi[ti].p]];
        int y=++cnt[mdi[ti].col];
        if(!x) all--;
        if(y==1) all++;
    }
    swap(a[mdi[ti].p],mdi[ti].col);
}
int main()
{
    n=read();q=read();
    for(int i=1;i<=n;i++)
     a[i]=read();
    int qc=0,mc=0;
    for(int i=1;i<=q;i++)
    {
        char k=getchar();
        while(k!='Q'&&k!='R') k=getchar();
        if(k=='Q')
        {
            qry[++qc].l=read();qry[qc].r=read();
            qry[qc].ti=mc;qry[qc].id=qc;
        }
        if(k=='R')
        {
            mdi[++mc].p=read();mdi[mc].col=read();
        }
    }   
    int sn=pow(n,3.0/4.0);
    for(int i=1;i<=n;i++)
    {
        bl[i]=(i-1)/sn+1;
    }
    sort(qry+1,qry+1+qc,cmp);
    int now=0,l=1,r=0;
    for(int i=1;i<=qc;i++)
    {
        while(r<qry[i].r) add(++r);
        while(r>qry[i].r) del(r--);
        while(l<qry[i].l) del(l++);
        while(l>qry[i].l) add(--l);
        while(now<qry[i].ti) modi(i,++now);
        while(now>qry[i].ti) modi(i,now--);
        ans[qry[i].id]=all;
    }
    for(int i=1;i<=qc;i++)
     printf("%d
",ans[i]);
}