P2725 邮票 Stamps

Posted 2021-03-18 xcg123

原题链接  https://www.luogu.com.cn/problem/P2725

 

 

题目大意

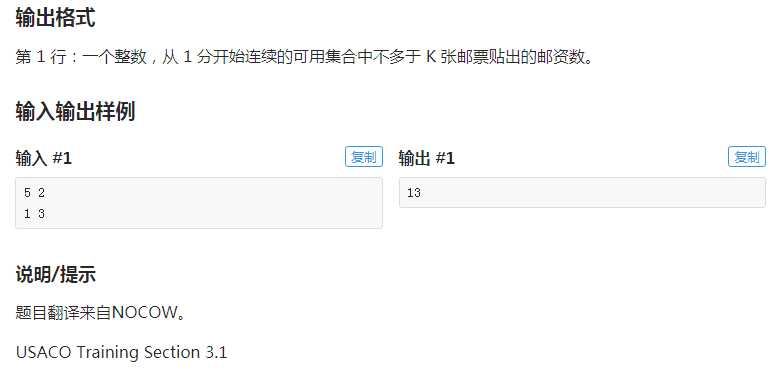
给你 m 个数，你可以从中任选不超过 n 个数（每个数可以重复选择），求最大的 k 使得 1~k 内的所有数都能被表示；

题解

70pts：

既然让求每个数能否被表示，那么我们可以顺着它的思路来设状态：

dp [ i ][ k ]：用 j 个数能否表达 k；

考虑怎么转移：

我们枚举所有的数 a [ j ]，如果说 i - a [ j ] 能用 k-1 个数来表达，那么我们再加上 a [ j ] 这个数就实现了用 k 个数表达 i；

给出状态转移方程的代码：

    for(int i=1;i<=n*maxn;i++)       //maxn是最大面值再+1 
    {
        for(int j=1;j<=m;j++)
        {
            if(i-a[j]<0) continue;
            for(int k=1;k<=n;k++)
            {
                dp[i][k]|=dp[i-a[j]][k-1];
            }
        }
    }

考虑到空间复杂度 O ( nm * 最大面值 )，会 MLE 的；

我们可以考虑滚动数组优化！

我们看这个状态转移方程，可以发现更新 i 的时候只会用到 i - a [ j ] 的数据，而 a [ j ] 最大为 10000，所以我们可以将第一维降到 10000；

注意要随时清空之前的信息；

#include<iostream>
#include<cstdio>
using namespace std;
int read()
{
    char ch=getchar();
    int a=0,x=1;
    while(ch<‘0‘||ch>‘9‘)
    {
        if(ch==‘-‘) x=-x;
        ch=getchar();
    }
    while(ch>=‘0‘&&ch<=‘9‘)
    {
        a=(a<<1)+(a<<3)+(ch-‘0‘);
        ch=getchar();
    }
    return a*x;
}
const int N=205;
int n,m,maxn;
int a[N];
bool dp[10005][55];              //dp[i][j]:能否用j张邮票表示i 
int main()
{
    n=read();m=read();
    for(int i=1;i<=m;i++) 
    {
        a[i]=read();
        maxn=max(maxn,a[i]);     //求最大面值 
    }
    dp[0][0]=1;
    maxn++;                      //这里maxn要再+1,不然i与i-maxn不会同时出现的 
    for(int i=1;i<=n*maxn;i++)   
    {
        int can=0;               //这个数能否被表示 
        for(int k=0;k<=n;k++)    //清空原有的信息 
            dp[i%maxn][k]=0;
        for(int j=1;j<=m;j++)    //枚举每个数 
        {
            if(i-a[j]<0) continue;
            for(int k=1;k<=n;k++)//枚举用多少个数表示i 
            {
                dp[i%maxn][k]|=dp[(i-a[j])%maxn][k-1];  //状态转移方程 
                can|=dp[i%maxn][k];
            }
        }
        if(can==0)               //如果当前数不能被表示,输出前一个数并结束程序 
        {
            printf("%d
",i-1);
            return 0;
        }
    }
    return 0;
}

 

100pts：

这 100pts 的做法就有点巧妙了。

一个显然贪心策略：

用尽量少的数来表示 i 更优。

举个例子：

假如我们可以用 3 个数，有 2 种不同的面值：1，2；

对于 3，我们可以将其表示为：3 = 1 + 1 + 1，这样的表示方法用了 3 个数；

但我们还可以这么表示：3 = 2 + 1，这样的表示方法只用了 2 个数；

如果我们采用第一种表示方法的话，我们再继续表示 4 的话就要用到 4 个数了，是不合法的；

而如果我们采用第二种表示方法的话，我们可以合法的表示了：4 = 2 + 1 + 1；

甚至有一个更优解：4 = 2 + 2；

所以说，用越少的数来表示一个数，就会留出更多的空间来表示后面的数；

那么，我们就无需去记录那些用很多数来表示的情况，只记录每个数最少能用几个数表示就好了；

 

状态设置

dp [ i ]：i 最少能用几个数表示；

状态转移

和上面的思路一样，只不过数组维护的东西改了而已；

dp[i]=min(dp[i],dp[i-a[j]]+1);

答案输出

如果一个数 i，最少表示 i 的数超过了 n 个，那么就说明 i 这个数无法被表示，我们输出 i-1 并结束程序；

那么，这个题就被我们转化成了完全背包问题；

Code：

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int read()
{
    char ch=getchar();
    int a=0,x=1;
    while(ch<‘0‘||ch>‘9‘)
    {
        if(ch==‘-‘) x=-x;
        ch=getchar();
    }
    while(ch>=‘0‘&&ch<=‘9‘)
    {
        a=(a<<1)+(a<<3)+(ch-‘0‘);
        ch=getchar();
    }
    return a*x;
}
const int N=205;
int n,m;
int a[N];
int dp[2000005];                 //dp[i]:最少能用多少个数来表示i 
int main()
{
    n=read();m=read();
    for(int i=1;i<=m;i++) a[i]=read();
    memset(dp,0x3f,sizeof(dp));  //初始化 
    dp[0]=0;                     //边界条件 
    for(int i=1;i<=n*10000;i++)  //枚举的最大范围 
    {
        for(int j=1;j<=m;j++)
            if(i-a[j]>=0)
                dp[i]=min(dp[i],dp[i-a[j]]+1);     //状态转移方程 
        if(dp[i]>n)              //i这个数无法被表示 
        {
            printf("%d
",i-1);
            return 0;
        }
    }
    return 0;
}