数据结构之递归案例一
Posted lyn4ever
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构之递归案例一相关的知识,希望对你有一定的参考价值。
什么是递归?
顾名思义,所谓递归就是一个函数(或方法)自己调用自己,最简的如下:
public void text() {
text();
}- 就是这么简单,但是一定要给这个递归函数一个出口,不然就会无限循环下去,最后的结果就是OutOfMemory(内存溢出),如果是在main函数中调用的话,就会出现栈空间已满的错误。
- 如何给一个递归的方法写一个出口呢?
只要在递归的过程中,有一个方法有一条return 语句,也就是有一个递归方法不再进行递归就会退出了。
我们给上方法添加一个返回的条件;
private int count = 0;
/*
* 每次让count累加,当它等于4时,就返回,这样就能这个递归函数了
*/
public void text() {
if (count == 4) {
return;
}
count++;
text();
}递归有什么用?
1.最著名的就是裴波那契数列
有如下问题:假设第一个月有一对刚出生的兔子,第二个月兔子进入成熟期,我三个月开始生育小兔子,而一对成熟的兔子会在每月生育一对小兔子,兔子永远不会死去。。。n月后会有多少只兔子
可以很容易地使用穷举来计算刚开始的几个月的兔子数
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 兔子对数 | 1 | 1 | 2 | 3 | 5 | 8 | 13 |
- 使用递归来解决这个问题的思路分析:
很容易得到一个算式就是:
当n=0时,有0对兔子;
当n=1时,有1对兔子;
当n=2时,有1对兔子,因为它是第三个月才开始生小兔子的
当n>2时,F(n)=F(n-1)+F(n-2)
当有了上面的式子后,我们就很容易地写出了如下代码:
public static int brithNew(int n) {
if (n < 0) {
return -1;
}
if (n == 0) {
return 0;
}
//这个其实就是递归退出的条件,因为n一直的在递减
if (n <= 2) {
return 1;
}
return brithNew(n-1)+brithNew(n-2);
}2.使用递归解决迷宫问题
先使用二维数组定义一个迷宫,有如下约定:
- 先使用0来表示这个迷宫中的所有位置
- 使用1来表示最外层的墙
- 使用2来表示这个点位已经走过了,而且是通的
- 使用3来表示这个点位已经走过,但是不通
定义的迷宫如下图:
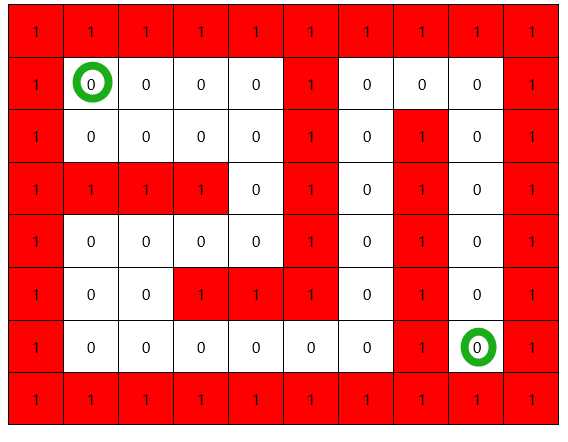
图中红色的部分表示墙,要从左上角移动到右下角,先使用二维数组定义一个迷宫。
private static void init(int[][] maze) {
//定义所有的墙
for (int i = 0; i < 10; i++) {
maze[0][i] = 1;
maze[7][i] = 1;
}
for (int i = 0; i < 8; i++) {
maze[i][0] = 1;
maze[i][9] = 1;
}
maze[3][1] = 1;
maze[3][2] = 1;
maze[3][3] = 1;
maze[5][3] = 1;
maze[5][4] = 1;
maze[5][5] = 1;
maze[4][5] = 1;
maze[3][5] = 1;
maze[2][5] = 1;
maze[1][5] = 1;
maze[2][7] = 1;
maze[3][7] = 1;
maze[4][7] = 1;
maze[5][7] = 1;
maze[6][7] = 1;
}打印下这个数组,就和上边的图片一样,如下:
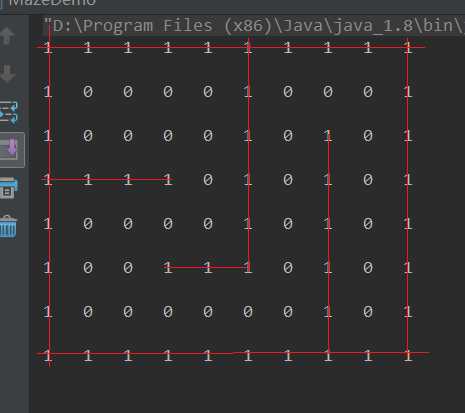
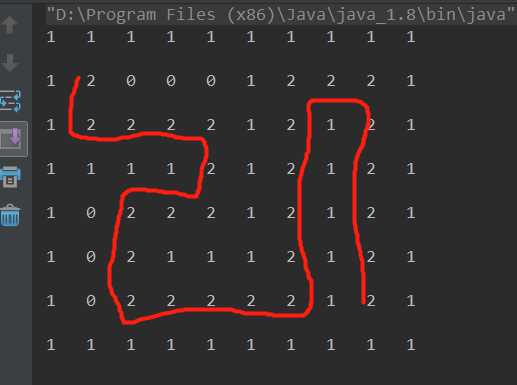
然后就开始找寻路径,具体有如下规则
- 每一个点都有下、右、上、左四条路径可选择,这个顺序是可以改变的;
- 更换这四个顺序,就会有不同的结果,所以可以试着更换这四个顺序来求现最短路径
- 当走到这个点时,我们先假设这个路径点是正确的,就是先给它赋值为2
- 每一个小递归退出的条件就是终点的值为2,即maze[9][7]==2
- 如果这个条路不通,就将当前这个点设置为3
private static boolean searchRoute(int maze[][], int x, int y) {
int i = maze.length;
int j = maze[0].length;
if (maze[i - 2][j - 2] == 2) {
//目标点的值为2,就说明这条路已经走完了
return true;
} else {
if (maze[x][y] == 0) {//为0说明这这条可走,而且没有走过
maze[x][y] = 2;
//按照下、右、上、左的顺序
if (searchRoute(maze, x + 1, y)) {//向下
return true;
} else if (searchRoute(maze, x, y+1)) {//向右
return true;
} else if (searchRoute(maze, x - 1, y)) {//向上
return true;
} else if (searchRoute(maze, x, y - 1)) {//向左
return true;
} else {
maze[x][y] = 3;
return false;
}
} else {
return false;
}
}
}
上边用到的打印数组的代码为:
public static void printlnArr(int arr[][]) {
for (int i = 0; i < arr.length; i++) {
for (int j = 0; j < arr[i].length; j++) {
System.out.print(arr[i][j] + " ");
}
System.out.println();
System.out.println();
}
}
以上是关于数据结构之递归案例一的主要内容,如果未能解决你的问题,请参考以下文章