Topological Sort (25分)

Posted 2021-03-17 nonlinearthink

Write a program to find the topological order in a digraph.

Format of functions:

bool TopSort( LGraph Graph, Vertex TopOrder[] );

where LGraph is defined as the following:

typedef struct AdjVNode *PtrToAdjVNode; 
struct AdjVNode{
    Vertex AdjV;
    PtrToAdjVNode Next;
};

typedef struct Vnode{
    PtrToAdjVNode FirstEdge;
} AdjList[MaxVertexNum];

typedef struct GNode *PtrToGNode;
struct GNode{  
    int Nv;
    int Ne;
    AdjList G;
};
typedef PtrToGNode LGraph;

The topological order is supposed to be stored in TopOrder[] where TopOrder[i] is the i-th vertex in the resulting sequence. The topological sort cannot be successful if there is a cycle in the graph -- in that case TopSort must return false; otherwise return true.

Notice that the topological order might not be unique, but the judge‘s input guarantees the uniqueness of the result.

Sample program of judge:

#include <stdio.h>
#include <stdlib.h>

typedef enum {false, true} bool;
#define MaxVertexNum 10  /* maximum number of vertices */
typedef int Vertex;      /* vertices are numbered from 0 to MaxVertexNum-1 */

typedef struct AdjVNode *PtrToAdjVNode; 
struct AdjVNode{
    Vertex AdjV;
    PtrToAdjVNode Next;
};

typedef struct Vnode{
    PtrToAdjVNode FirstEdge;
} AdjList[MaxVertexNum];

typedef struct GNode *PtrToGNode;
struct GNode{  
    int Nv;
    int Ne;
    AdjList G;
};
typedef PtrToGNode LGraph;

LGraph ReadG(); /* details omitted */

bool TopSort( LGraph Graph, Vertex TopOrder[] );

int main()
{
    int i;
    Vertex TopOrder[MaxVertexNum];
    LGraph G = ReadG();

    if ( TopSort(G, TopOrder)==true )
        for ( i=0; i<G->Nv; i++ )
            printf("%d ", TopOrder[i]);
    else
        printf("ERROR");
    printf("
");

    return 0;
}

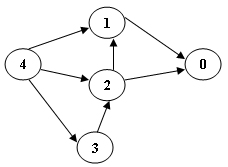
/* Your function will be put here */

Sample Input 1 (for the graph shown in the figure):

5 7
1 0
4 3
2 1
2 0
3 2
4 1
4 2

Sample Output 1:

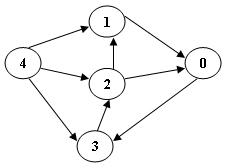
4 3 2 1 0 

Sample Input 2 (for the graph shown in the figure):

5 8
0 3
1 0
4 3
2 1
2 0
3 2
4 1
4 2

Sample Output 2:

ERROR

第一版的代码没有过，是因为超时，原因是我写了一个O(V^2)的算法，这道题必须要使用O(V+E)的算法。

int Incoming[MaxVertexNum];
int Queue[MaxVertexNum], head = 0, tail = 0;

bool FindNextIncomingZero(LGraph Graph) {
    for (int i = 0; i < Graph->Nv; i++) {
        if (!Incoming[i]) Queue[tail++] = i, Incoming[i]--;
    }
}

bool TopSort(LGraph Graph, Vertex TopOrder[]) {
    for (int i = 0; i < Graph->Nv; i++) {
        for (PtrToAdjVNode ptr = Graph->G[i].FirstEdge; ptr != NULL; ptr = ptr->Next) {
            Incoming[ptr->AdjV]++;
        }
    }

    FindNextIncomingZero(Graph);
    int temp = 0;
    while (head < tail) {
        TopOrder[temp++] = Queue[head++];
        for (PtrToAdjVNode ptr = Graph->G[Queue[head - 1]].FirstEdge; ptr != NULL; ptr = ptr->Next) {
            Incoming[ptr->AdjV]--;
        }
        FindNextIncomingZero(Graph);
    }

    return temp==Graph->Nv;
}

注意到其实在第一版的代码中FindNextIncomingZero这个函数是多余的，完全可以把这个函数合并到while循环中，这样就好了：

int Incoming[MaxVertexNum];
int Queue[MaxVertexNum], head = 0, tail = 0;

bool TopSort( LGraph Graph, Vertex TopOrder[] ){
    for(int i=0;i<Graph->Nv;i++)
        for(PtrToAdjVNode ptr = Graph->G[i].FirstEdge;ptr!=NULL;ptr = ptr->Next)
            Incoming[ptr->AdjV]++;

    for(int i=0;i<Graph->Nv;i++)
        if(!Incoming[i]) Queue[tail++] = i,Incoming[i]--;

    int temp=0;
    while(head<tail){
        TopOrder[temp++]=Queue[head++];
        for(PtrToAdjVNode ptr = Graph->G[Queue[head-1]].FirstEdge;ptr!=NULL;ptr = ptr->Next)
            if(!--Incoming[ptr->AdjV]) Queue[tail++] = ptr->AdjV,Incoming[ptr->AdjV]--;
    }

    if(temp!=Graph->Nv) return false;
    return true;
}