稠密线性方程求解

Posted 2021-03-17 lovebay

一、稠密矩阵分解

方法有PartialPivLU、FullPivLU、HouseholderQR、ColPivHouseholderQR、FullPivHouseholderQR、CompleteOrthogonalDecomposition、LLT、LDLT、BDCSVD、JacobiSVD、

 

 

 

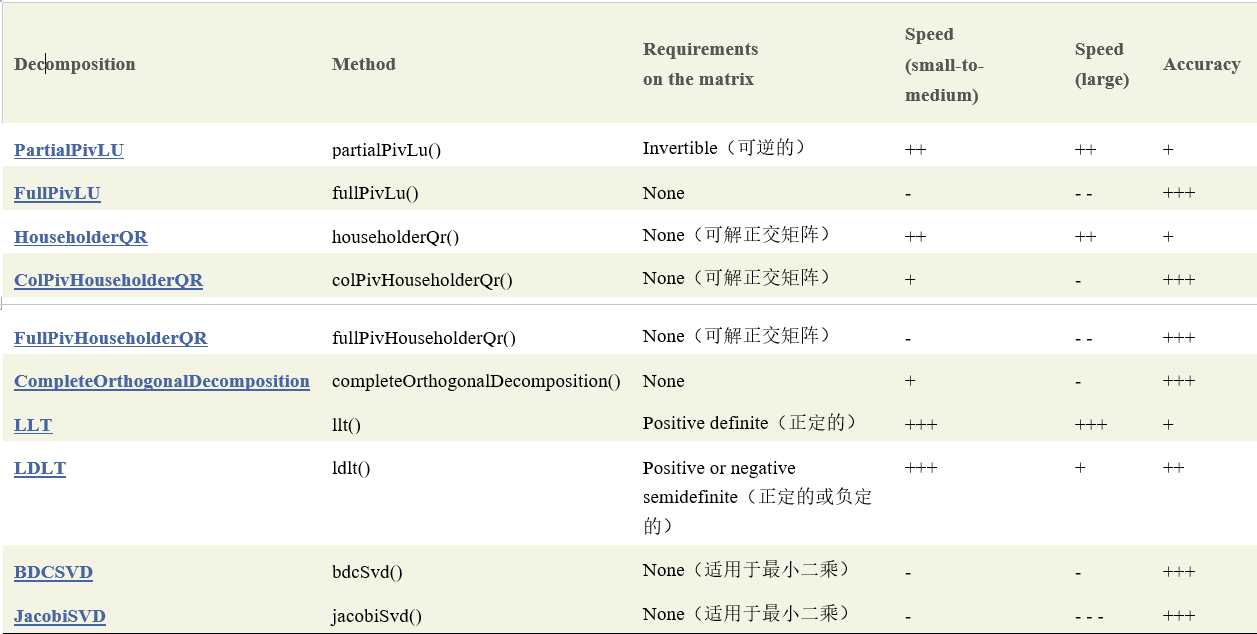
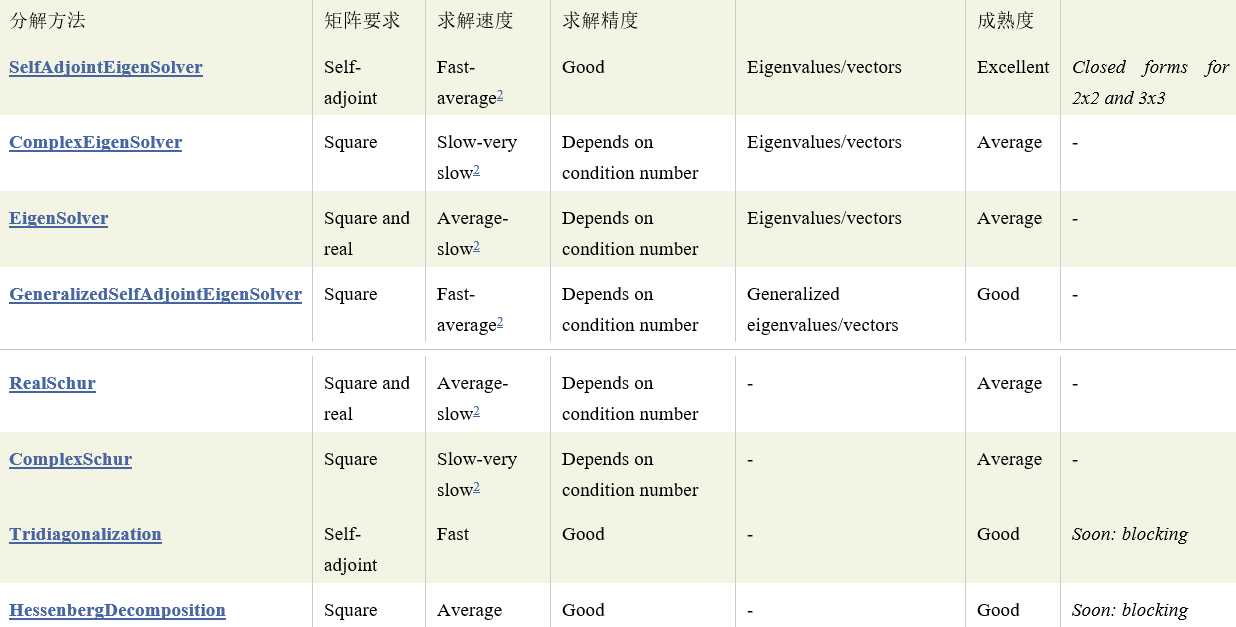
 以下线性求解器eigen没有提供

 

 

 

示例：

1、colPivHouseholderQr()

#include <iostream>

#include <Eigen/Dense>

using namespace std;

using namespace Eigen;

int main()

{

Matrix3f A;

Vector3f b;

A << 1,2,3, 4,5,6, 7,8,10;

b << 3, 3, 4;

cout << "Here is the matrix A: " << A << endl;

cout << "Here is the vector b: " << b << endl;

Vector3f x = A.colPivHouseholderQr().solve(b);

cout << "The solution is: " << x << endl;

}

 

2、ldlt()

#include <iostream>

#include <Eigen/Dense>

using namespace std;

using namespace Eigen;

int main()

{

Matrix2f A, b;

A << 2, -1, -1, 3;

b << 1, 2, 3, 1;

cout << "Here is the matrix A: " << A << endl;

cout << "Here is the right hand side b: " << b << endl;

Matrix2f x = A.ldlt().solve(b);

cout << "The solution is: " << x << endl;

}

 

3、fullPivLu()

#include <iostream>

#include <Eigen/Dense>

using namespace std;

using namespace Eigen;

int main()

{

MatrixXd A = MatrixXd::Random(100,100);

MatrixXd b = MatrixXd::Random(100,50);

MatrixXd x = A.fullPivLu().solve(b);

double relative_error = (A*x - b).norm() / b.norm(); // norm() is L2 norm

cout << "The relative error is: " << relative_error << endl;

}

 

4、计算特征值和特征向量eigenvalues  eigenvectors

#include <iostream>

#include <Eigen/Dense>

using namespace std;

using namespace Eigen;

int main()

{

Matrix2f A;

A << 1, 2, 2, 3;

cout << "Here is the matrix A: " << A << endl;

SelfAdjointEigenSolver<Matrix2f> eigensolver(A);

if (eigensolver.info() != Success) abort();

cout << "The eigenvalues of A are: " << eigensolver.eigenvalues() << endl;

cout << "Here‘s a matrix whose columns are eigenvectors of A "

<< "corresponding to these eigenvalues: "

<< eigensolver.eigenvectors() << endl;

}

 

5、计算逆和行列式  inverse and determinant

#include <iostream>

#include <Eigen/Dense>

using namespace std;

using namespace Eigen;

int main()

{

Matrix3f A;

A << 1, 2, 1,

2, 1, 0,

-1, 1, 2;

cout << "Here is the matrix A: " << A << endl;

cout << "The determinant of A is " << A.determinant() << endl;

cout << "The inverse of A is: " << A.inverse() << endl;

}

 

6、计算最小二乘解bdcSvd  JacobiSVD

 

#include <iostream>

#include <Eigen/Dense>

using namespace std;

using namespace Eigen;

int main()

{

MatrixXf A = MatrixXf::Random(3, 2);

cout << "Here is the matrix A: " << A << endl;

VectorXf b = VectorXf::Random(3);

cout << "Here is the right hand side b: " << b << endl;

cout << "The least-squares solution is: "

<< A.bdcSvd(ComputeThinU | ComputeThinV).solve(b) << endl;

}

 

7、LLT

#include <iostream>

#include <Eigen/Dense>

using namespace std;

using namespace Eigen;

int main()

{

Matrix2f A, b;

LLT<Matrix2f> llt;

A << 2, -1, -1, 3;

b << 1, 2, 3, 1;

cout << "Here is the matrix A: " << A << endl;

cout << "Here is the right hand side b: " << b << endl;

cout << "Computing LLT decomposition..." << endl;

llt.compute(A);

cout << "The solution is: " << llt.solve(b) << endl;

A(1,1)++;

cout << "The matrix A is now: " << A << endl;

cout << "Computing LLT decomposition..." << endl;

llt.compute(A);

cout << "The solution is now: " << llt.solve(b) << endl;

}

 

线性最小二乘的求解

       下面讨论线性最小二乘的求解的三种方法的使用---SVD分解、QR分解、法线方程。

SVD分解

#include <iostream>

#include <Eigen/Dense>

using namespace std;

using namespace Eigen;

int main()

{

MatrixXf A = MatrixXf::Random(3, 2);

cout << "Here is the matrix A: " << A << endl;

VectorXf b = VectorXf::Random(3);

cout << "Here is the right hand side b: " << b << endl;

cout << "The least-squares solution is: "

<< A.bdcSvd(ComputeThinU | ComputeThinV).solve(b) << endl;

}

    还有一种方法JacobiSVD速度慢些。

QR分解

MatrixXf A = MatrixXf::Random(3, 2);

VectorXf b = VectorXf::Random(3);

cout << "The solution using the QR decomposition is: "

<< A.colPivHouseholderQr().solve(b) << endl;

HouseholderQR (no pivoting, so fast but unstable), ColPivHouseholderQR (column pivoting, thus a bit slower but more accurate) and FullPivHouseholderQR (full pivoting, so slowest and most stable)

法线方程     A^TAx = A^Tb

MatrixXf A = MatrixXf::Random(3, 2);

VectorXf b = VectorXf::Random(3);

cout << "The solution using normal equations is: "

<< (A.transpose() * A).ldlt().solve(A.transpose() * b) << endl;

 

小结：the SVD decomposition is generally the most accurate but the slowest, normal equations is the fastest but least accurate, and the QR decomposition is in between.