深度学习之BN（批量标准化）

Posted 2021-03-16 jimchen1218

     BN作为最近一年来深度学习的重要成果，已经广泛被证明其有效性和重要性。虽然还解释不清其理论原因，但是实践证明好用才是真的好。

一、什么是BN

     机器学习领域有个很重要的假设：独立同分布假设，就是假设训练数据和测试数据是满足相同分布的，这是通过训练数据获得的模型能够在测试集获得好的效果的一个基本保障。BN就是深度神经网络训练过程中使得每层网络的输入保持相同分布。

二、为什么要使用BN

     根据论文《Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift》所讲内容，BN主要是解决Internal Convariate Shift问题。那么什么是Internal Convariate Shift呢? 可以这样解释：如果ML系统实例集合<X,Y>中的输入值X的分布老是变，这不符合IID假设，网络模型很难学习到有效的规律。对于深度学习这种包含很多隐层的网络结构，在训练过程中，因为各层参数不停在变化，所以每个隐层都会面临covariate shift的问题，也就是在训练过程中，隐层的输入分布老是变来变去，这就是所谓的“Internal Covariate Shift”，Internal指的是深层网络的隐层，是发生在网络内部的事情，而不是covariate shift问题只发生在输入层。由此提出了BN：让每个隐层节点的激活输入分布在固定区域。

      图像白化：对输入数据分布变换到0均值，1方差的正态分布。在神经网络的输入层中引入白化操作后收敛会加快，所以，进一步想：如果在神经网络的各层都加入，是不是可以较快的提高收敛速度呢？这就是提出BN的最初想法。

       BN的基本思想：深层神经网络在做非线性变换前的激活输入值（就是y=Wx+B，x是输入）随着网络深度加深或者在训练过程中，其分布逐渐发生偏移或者变动，之所以训练收敛慢，一般是整体分布逐渐往非线性函数的取值区间的上下限两端靠近。

       对于Sigmoid函数来说，意味着激活输入值Wx+B是大的负值或正值，所以这导致反向传播时低层神经网络的梯度消失，这是训练深层神经网络收敛越来越慢的本质原因.BN就是通过一定的规范化手段，把每层神经网络任意神经元这个输入值的分布强行拉回到均值为0方差为1的标准正态分布，其实就是把越来越偏的分布强制拉回比较标准的分布，这样使得激活输入值落在非线性函数对输入比较敏感的区域，这样输入的小变化就会导致损失函数较大的变化，意思是这样让梯度变大，避免梯度消失问题产生，而且梯度变大意味着学习收敛速度快，能大大加快训练速度。BN说到底就是这个机制，方法很简单，道理很深刻。

      把激活输入x调整到这个正态分布有什么用？首先我们看下均值为0，方差为1的标准正态分布代表什么含义：

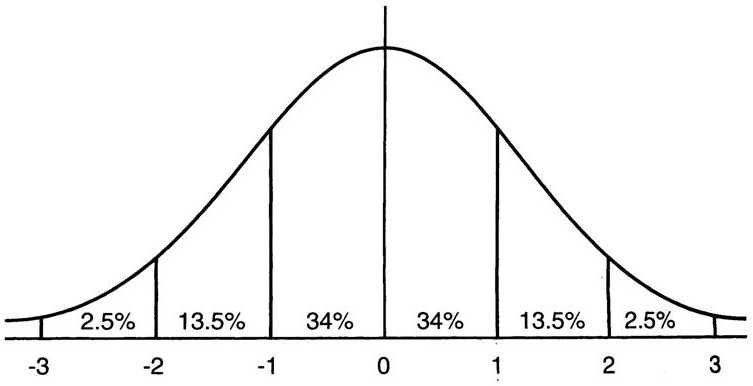
图:均值为0方差为1的标准正态分布图

　　这意味着在一个标准差范围内，也就是说64%的概率x其值落在[-1,1]的范围内，在两个标准差范围内，也就是说95%的概率x其值落在了[-2,2]的范围内。那么这又意味着什么？我们知道，激活值x=WU+B,U是真正的输入，x是某个神经元的激活值，假设非线性函数是sigmoid，那么看下sigmoid(x)其图形：

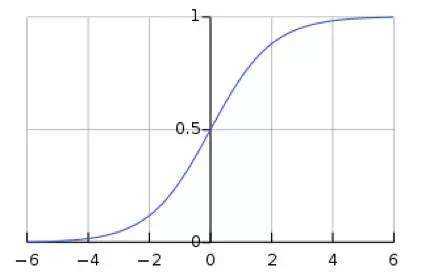
图: Sigmoid(x)

及sigmoid(x)的导数为：G’=f(x)*(1-f(x))，因为f(x)=sigmoid(x)在0到1之间，所以G’在0到0.25之间，其对应的图如下：

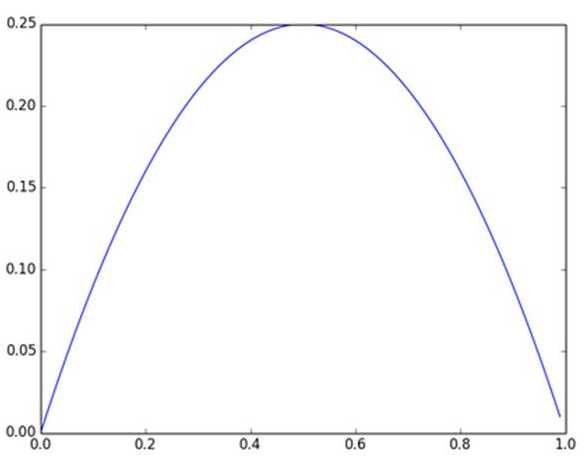
图:Sigmoid(x)导数图

　　假设没有经过BN调整前x的原先正态分布均值是-6，方差是1，那么意味着95%的值落在了[-8,-4]之间，那么对应的Sigmoid（x）函数的值明显接近于0，这是典型的梯度饱和区，在这个区域里梯度变化很慢，为什么是梯度饱和区？请看下sigmoid(x)如果取值接近0或者接近于1的时候对应导数函数取值，接近于0，意味着梯度变化很小甚至消失。而假设经过BN后，均值是0，方差是1，那么意味着95%的x值落在了[-2,2]区间内，很明显这一段是sigmoid(x)函数接近于线性变换的区域，意味着x的小变化会导致非线性函数值较大的变化，也即是梯度变化较大，对应导数函数图中明显大于0的区域，就是梯度非饱和区。

　　从上面几个图应该看出来BN在干什么了吧？其实就是把隐层神经元激活输入x=WU+B从变化不拘一格的正态分布通过BN操作拉回到了均值为0，方差为1的正态分布，即原始正态分布中心左移或者右移到以0为均值，拉伸或者缩减形态形成以1为方差的图形。什么意思？就是说经过BN后，目前大部分Activation的值落入非线性函数的线性区内，其对应的导数远离导数饱和区，这样来加速训练收敛过程。

　　但是很明显，看到这里，稍微了解神经网络的读者一般会提出一个疑问：如果都通过BN，那么不就跟把非线性函数替换成线性函数效果相同了？这意味着什么？我们知道，如果是多层的线性函数变换其实这个深层是没有意义的，因为多层线性网络跟一层线性网络是等价的。这意味着网络的表达能力下降了，这也意味着深度的意义就没有了。所以BN为了保证非线性的获得，对变换后的满足均值为0方差为1的x又进行了scale加上shift操作(y=scale*x+shift)，每个神经元增加了两个参数scale和shift参数，这两个参数是通过训练学习到的，意思是通过scale和shift把这个值从标准正态分布左移或者右移一点并长胖一点或者变瘦一点，每个实例挪动的程度不一样，这样等价于非线性函数的值从正中心周围的线性区往非线性区动了动。核心思想应该是想找到一个线性和非线性的较好平衡点，既能享受非线性的较强表达能力的好处，又避免太靠非线性区两头使得网络收敛速度太慢。