POJ-1330&HDU-2586 最近公共祖先（不带权+带权）树剖式写法求LCA

Posted 2021-03-16 lonely-wind-

其实敲树剖敲多了就会手敲，然后就发现其实树剖也是可以求LCA的，根据树剖的经验，我们两遍dfs后关于询问l,r的情况我们就开始跳链，当l,r处于同一个链的时候返回深度较小的那个点就好了，这里给个例题：

题目链接：http://poj.org/problem?id=1330

Description

A rooted tree is a well-known data structure in computer science and engineering. An example is shown below: 

 
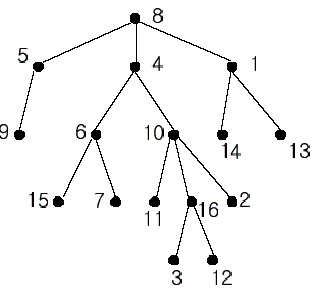
In the figure, each node is labeled with an integer from {1, 2,...,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is. 

For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y. 

Write a program that finds the nearest common ancestor of two distinct nodes in a tree. 

Input

The input consists of T test cases. The number of test cases (T) is given in the first line of the input file. Each test case starts with a line containing an integer N , the number of nodes in a tree, 2<=N<=10,000. The nodes are labeled with integers 1, 2,..., N. Each of the next N -1 lines contains a pair of integers that represent an edge --the first integer is the parent node of the second integer. Note that a tree with N nodes has exactly N - 1 edges. The last line of each test case contains two distinct integers whose nearest common ancestor is to be computed.

Output

Print exactly one line for each test case. The line should contain the integer that is the nearest common ancestor.

Sample Input

2
16
1 14
8 5
10 16
5 9
4 6
8 4
4 10
1 13
6 15
10 11
6 7
10 2
16 3
8 1
16 12
16 7
5
2 3
3 4
3 1
1 5
3 5

Sample Output

4
3



其题目大意是给你T组数据，n，n-1条边，其中第一个点是第二个点的父节点，最后询问a,b的最近公共祖先
那么我们先找到根节点，即没有父节点的那个点就是了，然后走一波树剖的准备过程。。。
以下是树剖式AC代码：

#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;

const int mac=1e4+10;

struct node
{
    int to,next;
}eg[mac<<1];
int head[mac],num=0,top[mac],son[mac],dson[mac];
int father[mac],d[mac],cnt=0,f[mac];

void add(int u,int v)
{
    eg[++num]=node{v,head[u]};
    head[u]=num;
}

void dfs2(int x,int tp)
{
    top[x]=tp;
    if (!dson[x]) return;
    dfs2(dson[x],tp);
    for (int i=head[x]; i!=-1; i=eg[i].next){
        int v=eg[i].to;
        if (v==father[x] || v==dson[x]) continue;
        dfs2(v,v);
    }
}

void dfs1(int x,int fa,int dp)
{
    d[x]=dp;father[x]=fa;son[x]=1;
    int maxson=-1;
    for (int i=head[x]; i!=-1; i=eg[i].next){
        int v=eg[i].to;
        if (v==fa) continue;
        dfs1(v,x,dp+1);
        son[x]+=son[v];
        if (son[v]>maxson) dson[x]=v,maxson=son[v];
    }
}

int lca(int l,int r)
{
    while (top[l]!=top[r]){
        if (d[top[l]]<d[top[r]]) swap(l,r);
        l=father[top[l]];
    }
    if (d[l]<d[r]) return l;
    return r;
}

void init()
{
        memset(head,-1,sizeof head);
        num=0;cnt=0;
        memset(f,0,sizeof f);
        memset(son,0,sizeof son);
        memset(dson,0,sizeof dson);
        memset(d,0,sizeof d);
        memset(top,0,sizeof top);
}

int main()
{
    //freopen("in.txt","r",stdin);
    int t;
    scanf ("%d",&t);
    while (t--){
        int n;
        scanf ("%d",&n);
        init();
        for (int i=1; i<=n-1; i++){
            int u,v;
            scanf("%d%d",&u,&v);
            add(u,v);add(v,u);f[v]=u;
        }
        int rt;
        for (int i=1; i<=n; i++) if (!f[i]) {rt=i;break;}
        dfs1(rt,0,1);
        dfs2(rt,rt);
        int l,r;
        scanf("%d%d",&l,&r);
        printf ("%d
",lca(l,r));
    }

    return 0;
}

View Code

 

接下来就是带权的情况了，实际上我们只需要多加一个dfs就好了，这个dfs求每个点到根节点的距离，那么我们求一波LCA,设该点为p,后用dis[l]+dis[r]-dis[p]*2就完事了。

给个例题：

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=2586

Problem Description

There are n houses in the village and some bidirectional roads connecting them. Every day peole always like to ask like this "How far is it if I want to go from house A to house B"? Usually it hard to answer. But luckily int this village the answer is always unique, since the roads are built in the way that there is a unique simple path("simple" means you can‘t visit a place twice) between every two houses. Yout task is to answer all these curious people.

 

Input

First line is a single integer T(T<=10), indicating the number of test cases.
  For each test case,in the first line there are two numbers n(2<=n<=40000) and m (1<=m<=200),the number of houses and the number of queries. The following n-1 lines each consisting three numbers i,j,k, separated bu a single space, meaning that there is a road connecting house i and house j,with length k(0<k<=40000).The houses are labeled from 1 to n.
  Next m lines each has distinct integers i and j, you areato answer the distance between house i and house j.

 

Output

For each test case,output m lines. Each line represents the answer of the query. Output a bland line after each test case.

 

Sample Input

2

3 2 

1 2 10

3 1 15

1 2

2 3

2 2

1 2 100

1 2

2 1

 

Sample Output

10

25

100

100

 

题目大意：T组数据，每组n,q，接下来n-1行，为u,v,w，接下来q行询问a到b的最短距离。

以下是AC代码：

#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;

const int mac=4e4+10;

struct node
{
    int to,next,w;
}eg[mac<<1];
int head[mac],num=0,top[mac],son[mac],dson[mac];
int father[mac],d[mac],cnt=0,dis[mac];

void add(int u,int v,int w)
{
    eg[++num]=node{v,head[u],w};
    head[u]=num;
}

void dfs2(int x,int tp)
{
    top[x]=tp;
    if (!dson[x]) return;
    dfs2(dson[x],tp);
    for (int i=head[x]; i!=-1; i=eg[i].next){
        int v=eg[i].to;
        if (v==father[x] || v==dson[x]) continue;
        dfs2(v,v);
    }
}

void dfs1(int x,int fa,int dp)
{
    d[x]=dp;father[x]=fa;son[x]=1;
    int maxson=-1;
    for (int i=head[x]; i!=-1; i=eg[i].next){
        int v=eg[i].to;
        if (v==fa) continue;
        dfs1(v,x,dp+1);
        son[x]+=son[v];
        if (son[v]>maxson) dson[x]=v,maxson=son[v];
    }
}

void dfs(int x)
{
    for (int i=head[x]; i!=-1; i=eg[i].next){
        int v=eg[i].to;
        if (v==father[x]) continue;
        dis[v]=dis[x]+eg[i].w;
        dfs(v);
    }
}

int lca(int l,int r)
{
    while (top[l]!=top[r]){
        if (d[top[l]]<d[top[r]]) swap(l,r);
        l=father[top[l]];
    }
    if (d[l]<d[r]) return l;
    return r;
}

void init()
{
        memset(head,-1,sizeof head);
        num=0;cnt=0;
        memset(son,0,sizeof son);
        memset(dson,0,sizeof dson);
        memset(d,0,sizeof d);
        memset(top,0,sizeof top);
}

int main()
{
    //freopen("in.txt","r",stdin);
    int t;
    scanf ("%d",&t);
    while (t--){
        int n,q;
        scanf ("%d%d",&n,&q);
        init();
        for (int i=1; i<=n-1; i++){
            int u,v,w;
            scanf("%d%d%d",&u,&v,&w);
            add(u,v,w);add(v,u,w);
        }
        int rt=1;
        dfs1(rt,0,1);
        dfs2(rt,rt);
        dfs(rt);
        int l,r;
        for (int i=1; i<=q; i++){
            scanf("%d%d",&l,&r);
            int anc=lca(l,r);
            printf("%d
",dis[l]+dis[r]-dis[anc]*2);
        }
    }

    return 0;
}

View Code