数据结构初探

Posted 2021-03-15 s3320

理解程序的本质

• 程序是为了实际的问题而存在
• 从本质上而言，程序是解决问题的步骤描述

首先理解实际问题

• 确认问题类型
• 确认求解的步骤

程序评鉴初探

• 用尽量少的内存空间解决问题
• 用尽量少的步骤解决问题

小结

• 程序是为了具体问题而存在的
• 程序需要围绕问题的解决进行设计
• 同一个问题可以有多种解决方案

数据结构起源

??数据结构主要研究非数值计算程序问题中的操作对象以及它们之间的关系。

• 计算机从解决数值计算问题到解决生活中的问题
• 现实生活中的问题涉及不同个体间的复杂联系
• 需要在计算机程序中描述生活中个体间的联系

关键概念

• 数据 – 程序的操作对象，用于描述客观事物 ，用于描述客观事物
• 数据的特点：
  • 可以输入到计算机
  • 可以被计算机程序处理
• 数据元素 – 组成数据的基本单位
• 数据项：一个数据元素由若干数据项组成 ：一个数据元素由若干数据项组成
• 数据对象 – 性质相同的数据元素的集合

struct Student              ===>            一种数据类型
{
    char* name;
    int age;
};

struct Student s;           ===>            数据元素

struct Student stu[100];    ===>            数据对象

s.name = "delphi Tang";     ===>            数据项
s.age = 30;

• 数据元素之间不是独立的，存在特定的关系，这些关系即结构
• 数据结构指数据对象中数据元素之间的关系
  • 如：数组中各个元素之间存在固定的线性关系

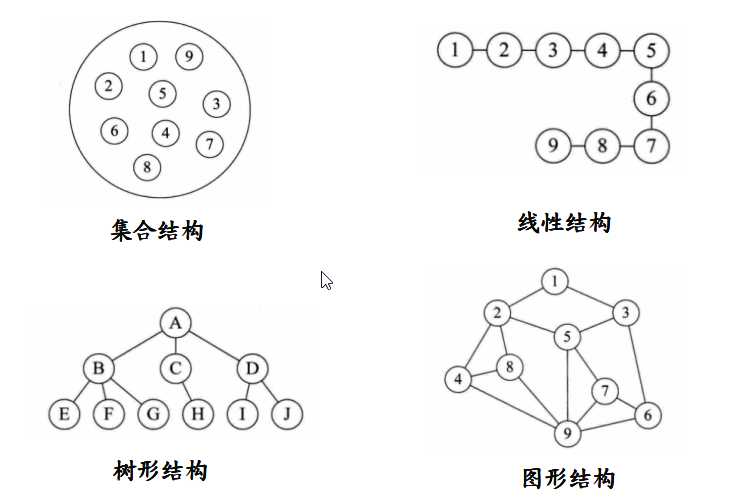
逻辑结构

• 集合结构
  • 数据元素之间没有特别的关系，仅同属相同集合
• 线性结构
  • 数据元素之间是一对一的关系
• 树形结构
  • 数据元素之间存在一对多的层次关系
• 图形结构
  • 数据元素之间是多对多的关系

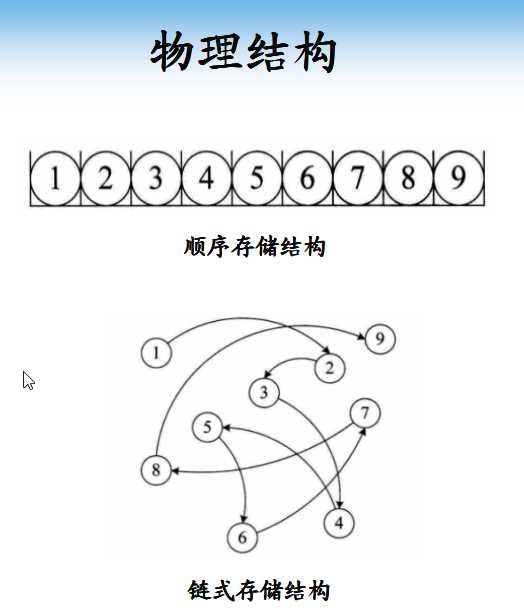
物理结构

??物理结构,逻辑结构在计算机中的存储形式

• 顺序存储结构
  • 将数据存储在地址连续的存储单元里
• 链式存储结构
  • 将数据存储在任意的存储单元里，通过保存地址的方式找到 ，通过保存地址的方式找到相关联的数据元素

小结

• 数据结构是相互之间存在一种或多种特定关系的数据元素的集合。
• 按照视点的不同，数据结构可以分为逻辑结构和物理 ，数据结构可以分为逻辑结构和物理结构。

逻辑结构	物理结构
集合结构	顺序结构
线性结构	链接结构
树形结构
图形结构

算法

数据结构与算法

• 数据结构只是静态的描述了数据元素之间的关系
• 高效的程序需要在数据结构的基础上设计和选择算法

高效的程序 = 恰当的数据结构 + 合适的算法

算法的定义

• 算法是特定问题求解步骤的描述
• 在计算机中表现为指令的有限序列
• 算法是独立存在的一种解决问题的方法和思想
• 对于算法而言，语言并不重要，重要的是思想

算法的特性

• 输入
  • 算法具有0个或多个输入
• 输出
  • 算法至少有1个或多个输出
• 有穷性
  • 算法在有限的步骤之后会自动结束而不会无限循环
• 确定性
  • 算法中的每一步都有确定的含义，不会出现二义性 ，不会出现二义性
• 可行性
  • 算法的每一步都是可行的

算法设计的准则

• 正确性
  1. 算法对于合法数据能够得到满足要求的结果
  2. 算法能够处理非法输入，并得到合理的结果 ，并得到合理的结果
  3. 算法对于边界数据和压力数据都能得到满足要求的结果
• 注意：
  1. 正确性是算法最需要满足的基本的准则，但是作为计算机程序，不可能无限制的满足这条准则 ，不可能无限制的满足这条准则。

算法设计的准则

• 可读性
  • 算法要方便阅读，理解和交流
• 健壮性
  • 算法不应该产生莫名其妙的结果
• 高性价比
  • 利用最少的时间和资源得到满足要求的结果
• 注意：
  • 算法可读性是最容易被忽视的，然而，程序是写给人看的，而不是计算机 ，而不是计算机。

小结

• 算法是为了解决实际问题而设计的
• 数据结构是算法需要处理的问题载体
• 数据结构与算法相辅相成

程序 = 数据结构 + 算法

审判程序的灵魂

算法效率的度量

事后统计法

• 比较不同算法对同一组输入数据的运行处理时间
• 缺陷
  • 为了获得不同算法的运行时间必须编写相应程序
  • 运行时间严重依赖硬件以及运行时的环境因素
  • 算法的测试数据的选取相当困难

事后统计法虽然直观，但是实施困难且缺陷多 ，但是实施困难且缺陷多，一般不予考虑。

事前分析估算

• 依据统计的方法对算法效率进行估算
• 影响算法效率的主要因素
  • 算法采用的策略和方法
  • 问题的输入规模
  • 编译器所产生的代码
  • 计算机执行速度

算法效率的简单估算

• 启示
  • 练习中的程序关键部分的操作数量为n*n
  • 三种求和算法中求和的关键部分的操作数量分别为2n, n和1

??随着问题规模n的增大，它们操作数量的差异 ，它们操作数量的差异会越来越大，因此实际算法在时间效率上的 ，因此实际算法在时间效率上的差异也会变得非常明显！

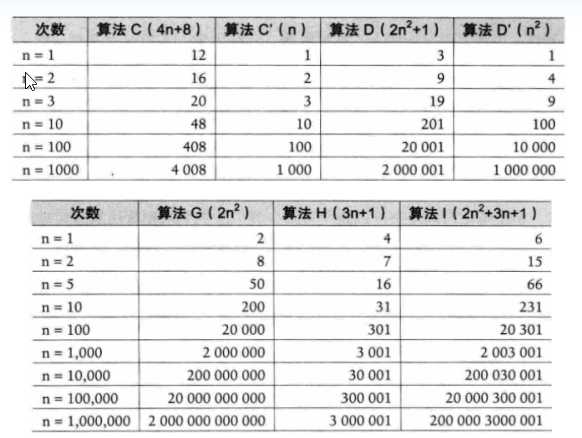
??判断一个算法的效率时，往往只需要关注操作数量的 ，往往只需要关注操作数量的
最高次项，其它次要项和常数项可以忽略 ，其它次要项和常数项可以忽略。

大O表示法

• 算法效率严重依赖于操作(Operation)数量
• 在判断时首先关注操作数量的最高次项
• 操作数量的估算可以作为时间复杂度的估算

O(5) = O(1)
O(2n + 1) = O(2n) = O(n)
O(n2 + n + 1) = O(n2)
O(3n3+1) = O(3n3) = O(n3)

常见时间复杂度类型

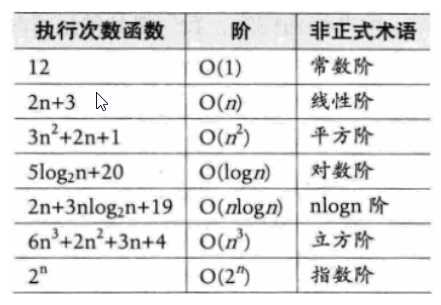
• 关系
  

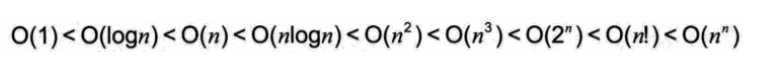
??在没有特殊说明时，我们所分析的算法的时 ，我们所分析的算法的时间复杂度都是指最坏时间复杂度。

算法的空间复杂度

??算法的空间复杂度通过计算算法的存储空间实现

S(n) = O(f(n))
其中，n为问题规模，f(n)为在问题规模为 为在问题规模为n时所占用存储空间的函数

大O表示法同样适用于算法的空间复杂度 表示法同样适用于算法的空间复杂度
当算法执行时所需要的空间是常数时，空间复杂度为 ，空间复杂度为O(1)

空间与时间的策略

• 多数情况下，算法执行时所用的时间更令人关注 ，算法执行时所用的时间更令人关注
• 如果有必要，可以通过增加空间复杂度来降低时间复杂度 ，可以通过增加空间复杂度来降低时间复杂度
• 同理，也可以通过增加时间复杂度来降低空间复杂度

??在实现算法时,需要分析具体问题对执行时间和空间的要求。
空间换时间 ? 时间换空间？