最短路问题--Floyd 畅通工程续

Posted 2021-03-15 very-beginning

畅通工程续

某省自从实行了很多年的畅通工程计划后，终于修建了很多路。不过路多了也不好，每次要从一个城镇到另一个城镇时，都有许多种道路方案可以选择，而某些方案要比另一些方案行走的距离要短很多。这让行人很困扰。

现在，已知起点和终点，请你计算出要从起点到终点，最短需要行走多少距离。

Input

本题目包含多组数据，请处理到文件结束。
每组数据第一行包含两个正整数N和M(0<N<200,0<M<1000)，分别代表现有城镇的数目和已修建的道路的数目。城镇分别以0～N-1编号。
接下来是M行道路信息。每一行有三个整数A,B,X(0<=A,B<N,A!=B,0<X<10000),表示城镇A和城镇B之间有一条长度为X的双向道路。
再接下一行有两个整数S,T(0<=S,T<N)，分别代表起点和终点。

Output

对于每组数据，请在一行里输出最短需要行走的距离。如果不存在从S到T的路线，就输出-1.

 

明天就要讲图论了，之前虽然听过一遍，但是没有搞懂，感觉很难的样子。介于之前本人还写过两三道有关树，最小生成树，树状数组这类的题，晚上就先预习一下最短路径问题，先就着这一道题来系统的梳理一下Floyd把

Floyd：

动态转移方程 dist[i][j] = min(dist[i][j],dist[i][k] + dist[k][j]);

初始化//dist[i][j] 表示从i到j之间的最短距离 

1 //dist[i][j] 表示从i到j之间的最短距离 
2 int dist[maxn][maxn]; 
3 for (int i = 0; i< n ;i++) 
4     for (int j = 0 ;j< n ;j++) 
5         dist[i][j] = edge[i][j];

时间复杂度 节点个数 N，边个数 M O(N3)

• 求所有节点到节点 1 的最短距离

 

 

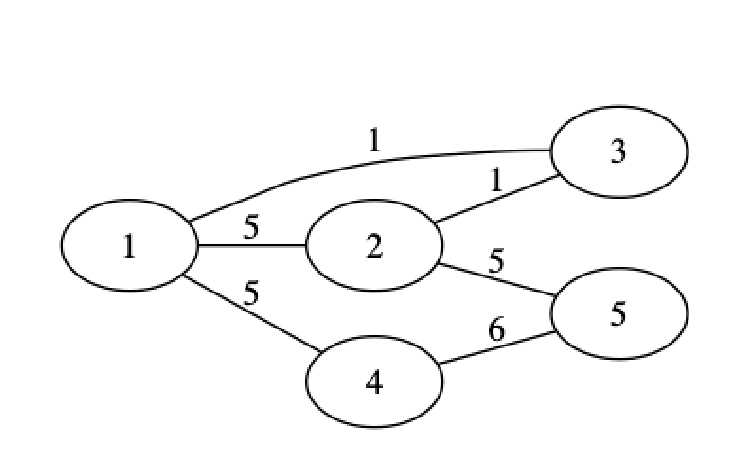
 1. 初始化
• dist 矩阵 – dist[i][j] 表示节点 i 到节点 j 之间的最短路径长度 – dist 初始化为 edge

 

 2. 流程
(a) step 1 • 通过节点 1 作为中转节点更新 dist • 更新公式 dist[i][j] = min(dist[i][1] + dist[1][j],dist[i][j]);

 

 (b) step 2 • 通过节点 2 作为中转节点更新 dist • 更新公式 dist[i][j] = min(dist[i][2] + dist[2][j],dist[i][j]);

 

 (c) step 3 • 通过节点 3 作为中转节点更新 dist • 更新公式 dist[i][j] = min(dist[i][3] + dist[3][j],dist[i][j]);

 

 

(d) step 4 • 通过节点 4 作为中转节点更新 dist • 更新公式 dist[i][j] = min(dist[i][4] + dist[4][j],dist[i][j]);

 

 (e) step 5 • 通过节点 5 作为中转节点更新 dist • 更新公式 dist[i][j] = min(dist[i][5] + dist[5][j],dist[i][j]);

 

 有一说一，这道题显然代码为：

 1 #include <iostream>
 2 #include <cstdio>
 3 #include <cmath>
 4 #include <cstring>
 5 #include <algorithm>
 6 using namespace std;
 7 int const maxn=1000;
 8 int const INF=1e9; 
 9 int dist[maxn][maxn];
10 int n,m; 
11 int floyd(int s,int t){    
12  for(int t = 0;t < n;t++)        
13      for(int i = 0;i < n;i++)            
14          for(int j = 0;j < n;j++)                
15          if(dist[i][j] > dist[i][t] + dist[t][j])                    
16              dist[i][j] = dist[i][t] + dist[t][j];    
17              if(dist[s][t] == INF)        
18              return -1;    
19              else       
20               return dist[s][t];
21 }
22 int main(){    
23     int a,b,x,s,t,ans;    
24     while(scanf("%d %d",&n,&m) != EOF)    {        
25         for(int i = 0;i < n;i++)            
26         for(int j = 0;j < n;j++)                
27             dist[i][j] = (i == j ? 0 : INF);        
28         while(m--)        
29         {            
30             scanf("%d %d %d",&a,&b,&x);            
31             if(x < dist[a][b])        
32                 dist[a][b] = dist[b][a] = x;        
33             }        
34             scanf("%d %d",&s,&t);        
35             ans = floyd(s,t);        
36             printf("%d
",ans);    
37             }    
38     return 0;
39 }