6442. GDOI2020模拟01.18钩子

Posted 2021-03-15 gmh77

题目描述

Description

Input

Output

Sample Input
Sample Input1
3 1000000007

Sample Input2
4 1000000007

Sample Output
Sample Output1
0 1 0
500000004 0 500000004
500000004 0 500000004

Sample Output2
0 500000004 500000004 0
333333336 166666668 166666668 333333336
333333336 166666668 166666668 333333336
333333336 166666668 166666668 333333336

Data Constraint

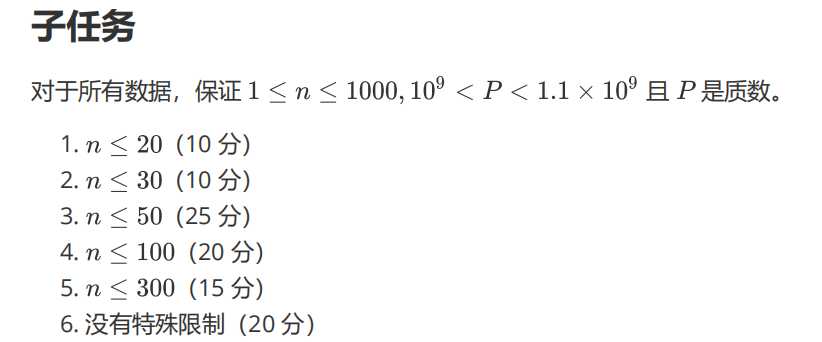
题解

怒刚3h爆0

可以发现，操作的段可以分成log层，不同层之间段的先后顺序固定，同一层的可以互换

随便模拟一下可以得到每一层的奇数段数s1和偶数段数s2，考虑计算本层的概率

设(f[i][j])表示已经放了i个奇数段，j个偶数段，那么当前可以放的位置数为((s1-i)+2(s2-j))，每个位置概率相等

设前面层的总人数为sum，那么在(f[i][j])转移时就轮到第(sum+i+j+1)个人，可以算出每个人放在奇数段和偶数段的概率

显然放在奇数段的时候每个奇数段被放到的概率相等，所以可以求出第(sum+1sim sum+s1+s2)个人的概率

往下做时，先假设偶数段只能放左边，做完之后把第(sum+s1+s2+1sim n)个人在偶数段中的对称位置概率平均一下即可

code

#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define add(a,b) a=((a)+(b))%mod
#define min(a,b) (a<b?a:b)
#define max(a,b) (a>b?a:b)
//#define file
using namespace std;

long long f[1001][1001];
long long g[1001][1001];
long long h[1002][2]; //0=odd 1=even
long long w[1001];
bool bz[1001];
int g1[21][1002];
int g2[21][1002];
int G[21][1002];
int n,i,j,k,l;
long long mod,Mod;

long long qpower(long long a,int b)
{
    long long ans=1;
    
    while (b)
    {
        if (b&1)
        ans=ans*a%mod;
        
        a=a*a%mod;
        b>>=1;
    }
    
    return ans;
}

void dg(int t,int sum)
{
    int i,j,k,l,mx=0,tot=0,s1=0,s2=0;
    
    fo(i,1,n) g1[t][i]=!bz[i]?g1[t][i-1]+1:0;
    fd(i,n,1) g2[t][i]=!bz[i]?g2[t][i+1]+1:0;
    fo(i,1,n) G[t][i]=min(g1[t][i],g2[t][i]);
    
    fo(i,1,n)
    mx=max(mx,G[t][i]);
    
    if (mx==1)
    {
        fo(i,1,n) tot+=!bz[i];
        
        fo(i,sum+1,n)
        {
            fo(j,1,n)
            if (!bz[j])
            f[i][j]=w[tot];
        }
        
        return;
    }
    
    fo(i,1,n)
    if (G[t][i]==mx)
    {
        if (G[t][i-1]!=mx && G[t][i+1]!=mx)
        ++s1;
        else
        if (G[t][i+1]==mx)
        ++s2;
    }
    
    memset(g,0,sizeof(g));
    g[0][0]=1;
    
    fo(i,0,s1)
    {
        fo(j,0,s2)
        if (i+j<=s1+s2)
        {
            if (i<s1)
            {
                add(g[i+1][j],g[i][j]*w[(s1-i)+(s2-j)*2]%mod*(s1-i)%mod);
                add(h[sum+i+j+1][0],g[i][j]*w[(s1-i)+(s2-j)*2]%mod*(s1-i)%mod);
            }
            if (j<s2)
            {
                add(g[i][j+1],g[i][j]*w[(s1-i)+(s2-j)*2]%mod*((s2-j)*2)%mod);
                add(h[sum+i+j+1][1],g[i][j]*w[(s1-i)+(s2-j)*2]%mod*((s2-j)*2)%mod);
            }
        }
    }
    
    fo(i,sum+1,sum+s1+s2)
    {
        fo(j,1,n-1)
        if (G[t][j]==mx)
        {
            if (G[t][j-1]!=mx && G[t][j+1]!=mx)
            f[i][j]=h[i][0]*w[s1]%mod;
            else
            if (G[t][j+1]==mx)
            {
                f[i][j]=h[i][1]*w[s2+s2]%mod;
                f[i][j+1]=h[i][1]*w[s2+s2]%mod;
            }
        }
    }
    
    fo(i,1,n)
    if (G[t][i]==mx && G[t][i-1]!=mx && G[t][i+1]!=mx || G[t][i]==mx && G[t][i+1]==mx)
    bz[i]=1;
    
    dg(t+1,sum+s1+s2);
    
    fo(j,1,n-1)
    if (G[t][j]==mx && G[t][j+1]==mx)
    {
        fo(i,sum+s1+s2,n)
        {
            fo(k,0,mx-1)
            {
                f[i][j-k]=(f[i][j-k]+f[i][j+k+1])*w[2]%mod;
                f[i][j+k+1]=f[i][j-k];
            }
        }
    }
}

int main()
{
    #ifdef file
    freopen("a.in","r",stdin);
    #endif
    
    scanf("%d%lld",&n,&mod);Mod=mod-2;
    
    w[1]=1;
    fo(i,2,1000)
    w[i]=mod-w[mod%i]*(mod/i)%mod;
    
    dg(1,0);
    
    fo(i,1,n)
    {
        fo(j,1,n)
        printf("%lld ",(f[i][j]+mod)%mod);
        printf("
");
    }
}