并查集

Posted 2021-03-15 nioh

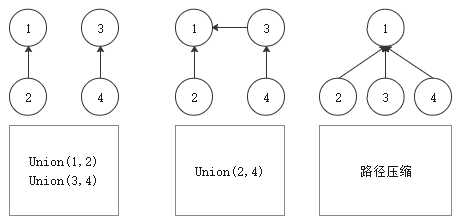
void init() {
    for(int i = 1; i <= N; i++)
        f[i] = i;
}

int find(int k) {
    return f[k] == k? k : f[k] = find(f[k]);
}

int union(int a, int b) {
    f[find(b)] = find(a);
}

 

带权并查集

假定a、b是两个结点且a > b，a -> b表示区间[b, a)的和，b -> a表示负的区间[b, a)的和。
需要将结点对转化为一种左开右闭的形式以方便连接。

假设W1是要添加的边，W4是实际添加的边，它们之间的关系如下图所示。

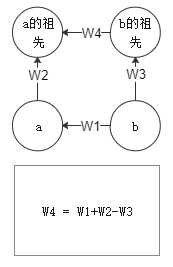
 对于路径压缩，直接累加各边权即可。

例题：HDU3038
http://acm.hdu.edu.cn/showproblem.php?pid=3038

//样例输入
10 5
1 10 100
7 10 28
1 3 32
4 6 41
6 6 1
 
//样例输出
1

将这个求解过程可视化。

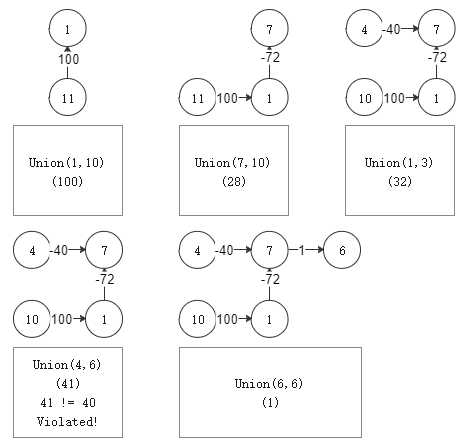
#include<bits/stdc++.h>
using namespace std;

int f[200010], w[200010];

int find(int k) {
    if(k != f[k]) {
        int a = find(f[k]);
        w[k] += w[f[k]];
        f[k] = a;
    }
    return f[k];
}

int N, M, A, B, S;
int main() {
    while(~scanf("%d%d", &N, &M)) {
        for(int i = 1; i <= N + 1; i++) {
            f[i] = i;
            w[i] = 0;
        }
        int ans = 0;
        while(M--) {
            scanf("%d%d%d", &A, &B, &S);
            B++;
            int Aa = find(A), Ba = find(B);
            if(Aa != Ba) {
                f[Ba] = Aa;
                w[Ba] = S + w[A] - w[B];
            }
            else if(w[B] - w[A] != S) ans++;
        }
        cout << ans << endl;
    }
}