有关强连通分量
Posted mgtnb
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了有关强连通分量相关的知识,希望对你有一定的参考价值。
定义
在有向图G中,如果两个顶点vi,vj间(vi>vj)有一条从vi到vj的有向路径,同时还有一条从vj到vi的有向路径,则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通,称G是一个强连通图。有向图的极大强连通子图,称为强连通分量(strongly connected components)。——以上来自百度百科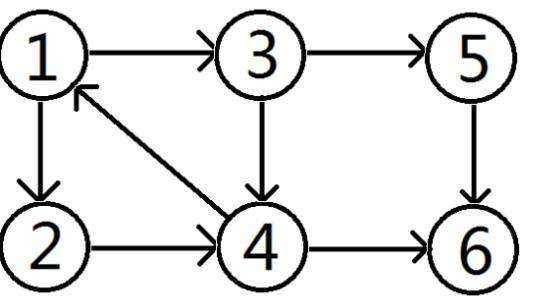
如上图,强连通分量有{1,2,3,4},{5},{6}。
Tarjan 算法
Tarjan算法基于有向图的深度优先遍历,能够在线性时间内求出一张图的各个强连通分量。
基本思路是对于每个点,找到与它一起能构成环的节点。一个环一定是强连通分量。
记录一个时间戳dfn[x],在深度优先遍历时,按每个节点第一次被访问的时间顺序依次标记。
维护一个栈。
x的追溯值low[x]记录x在栈中且存在一条从以x为根的子树出发以该点为终点的节点的最小时间戳。
当节点x第一次被访问时,将x入栈,初始化low[x]=dfn[x]。
找x的每一条出边y,如果y没被访问,则递归访问y,从y回溯后,令low[x]=min(low[x],low[y]);如果y被访问,且在栈中,则令low[x]=min(low[x],dfn[y])。
在x回溯之前,判断low[x]是否等于dfn[x],如果是,则不断弹出栈中元素,直至x被弹出。
此时弹出的所有节点,便构成了一个强连通分量,用一个vector型的scc[i]数组保存。
c[x]数组表示x所在的强连通分量的编号。
ins[x]数组记录x点是否入栈。
void tarjan(int x) { dfn[x]=low[x]=++num; stack[++top]=x; ins[x]=1; for(int i=head[x];i;i=next[i]) { int y=ver[i]; if(!dfn[y]) { tarjan(y); low[x]=min(low[x],low[y]); } else if(ins[y]) low[x]=min(low[x],dfn[y]); if(dfn[x]==low[x]) { cnt++;int k; do { k=stack[top--]; ins[k]=0; c[k]=cnt; scc[cnt].push_back(k); } while(x!=k) } } } for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i);
缩点
将有向图中的每个强连通分量缩成一个点。
对于每个强连通分量,在它们之间连一条边,得到一个有向无环图,保存在另一个邻接表中。
for(int x=1;x<=n;x++) { for(int i=head[x];i;i=next[i]) { int y=ver[i]; if(c[x]==c[y]) continue; add(c[x],c[y]);//保存在邻接表中 } }
Kosaraju 算法
首先有对于一张有向图,它的原图和反图的强连通分量是一样的。
利用此原理,Kosaraju算法先对原图做dfs,记录各点退出dfs的时间顺序
求反图。
对反图再次进行dfs,按照第一次保存的顺序由大到小访问顶点。
void dfs1(int x)
{
vis[x]=1;
for(int i=0;i<g[x].size();i++)
{
if(vis[g[x][i]])
dfs1(g[x][i]);
}
vs.push_back(x);
}
void dfs2(int x,int y)
{
vis[x]=y;
cmp[x]=y;
for(int i=0;i<rg[x].size();i++)
{
if(!vis[g2[x][i]])
dfs2(g2[x][i],y);
}
}
int scc()
{
memset(vis,0,sizeof(vis));
vs.clear();
for(int i=0;i<V;i++)
{
if(!vis[i])
dfs1(i);
}
memset(vis,0,sizeof(vis));
int k=0;
for(int i=vs.size()-1;i>=0;i--)
{
if(!vis[vs[i]])
dfs2(vs[i],k++);
}
return k;
}
一些例题
受欢迎的牛
https://www.luogu.com.cn/problem/P2341
模板题,用tarjan算法或者Kosaraju算法都可以。
真的很模板,就不贴代码了。
稳定婚姻
https://www.luogu.com.cn/problem/P1407
啧,不得不吐槽一下,这道题三观真不正。
建图,夫妻之间由man指向woman,情人之间由woman指向man(反过来也行)。
再判断强联通分量,如果夫妻之间在同一强连通分量中,就说明婚姻是不安全的,不在就是安全的。
#include<bits/stdc++.h> using namespace std; const int N=300002; map<string,int> a; int ver[N],next[N],head[N]; int dfn[N],low[N],s[N],ins[N],c[N]; int tot,cnt,idx,top; void add(int x,int y) { ver[++tot]=y; next[tot]=head[x]; head[x]=tot; } void tarjan(int x) { dfn[x]=low[x]=++idx; s[++top]=x; ins[x]=1; for(int i=head[x];i;i=next[i]) { int y=ver[i]; if(dfn[y]==0) { tarjan(y); low[x]=min(low[y],low[x]); } else if(ins[y]) low[x]=min(low[x],dfn[y]); } if(dfn[x]==low[x]) { cnt++; while(1) { c[s[top]]=cnt; ins[s[top]]=0; if(s[top--]==x) break; } } } int main() { int n,m ; scanf("%d",&n); string s1,s2; for(int i=1;i<=n ;i++) { cin>>s1>>s2; a[s1]=i; a[s2]=i+n; add(i,i+n); } scanf("%d",&m ); for(int i=1;i<=m ;i++) { cin>>s1>>s2; add(a[s2],a[s1]); } for(int i=1;i<=n*2;i++) { if(dfn[i]==0) tarjan(i); } for(int i=1;i<=n;i++) { if(c[i]==c[i+n]) puts("Unsafe"); else puts("Safe"); } return 0; }
HXY烧情侣
https://www.luogu.com.cn/problem/P2194
怎么最近做的题都奇奇怪怪的[不解]。
求强连通分量就行了,也挺模板的一道题。
#include<bits/stdc++.h>
using namespace std;
const int N=300005;
int n,w[N],m,ans1,ans2;
int ver[N],next[N],head[N],tot;
void add(int x,int y)
{
ver[++tot]=y;
next[tot]=head[x];
head[x]=tot;
}
const int mod=1e9+7;
int dfn[N],low[N],num,belong[N],all[N],cnt;
bool vis[N];
stack<int>s;
vector<int>G[N];
void tarjan(int x)
{
dfn[x]=low[x]=++num;
s.push(x);
vis[u]=1;
for(int i=head[x];i;i=next[i])
{
int y=ver[i];
if(!dfn[y])
{
tarjan(y);
low[x]=min(low[x],low[y]);
}
else if(vis[y])
low[x]=min(low[x],dfn[y]);
}
if(low[x]==dfn[y])
{
int k=x;
++cnt;
do{
v=s.top();s.pop();
vis[k]=c[k]=cnt;all[cnt]++;
G[cnt].push_back(k);
}while(k!=x);
}
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&w[i]);
scanf("%d",&m);
for(int a,b,i=1;i<=m;i++)
{
scanf("%d%d",&a,&b);
add(a,b);
}
for(int i=1;i<=n;i++)
if(!dfn[i]) tarjan(i);
ans2=1;
for(int i=1;i<=cnt;i++)
{
int l=G[i].size(),k=0,minn=999999999;
for(int j=0;j<l;j++)
{
if(w[G[i][j]]<minn)
{
minn=w[G[i][j]];
k=1;
}
else if(minn==w[G[i][j]] k++;
}
ans1+=minn;
ans2=(ans2%mod*k%mod)%mod;
}
printf("%d %d",ans1,ans2);
return 0;
}
我觉得差不多了 嗯。
赶在十点之前交。
新年快乐。
以上是关于有关强连通分量的主要内容,如果未能解决你的问题,请参考以下文章