编码的简单总结

Posted 2021-03-14 qi-lin

说明

• 下面对于各种编码分类并不完全对，仅仅为了便于比较总结记忆
• 编码的前缀也不是严格非要那样，为了在碰到时，或许可以一眼看出这是哪种编码
• 对于编码方式没有详细解释，只是简短的大概说明，关于编码具体过程，网上有很多资料
• utf编码有大小端的问题https://blog.csdn.net/byf0521hlyp/article/details/80365045
• base家族https://blog.csdn.net/lili13897741554/article/details/82177472

字符及网络上常用编码

编码	目的	前缀或特点	编码形式	常见或特殊记忆
url编码	对ascii中的一些可打印字符进行编码	前缀%	以％为前缀，其后是字符的两16进制的ascii码	％20空格 ％00空字节 ％25百分号 +也代表url的空格
html编码	为在html文档中安全的使用某些字符	&或&#或&#x	后跟字符10进制的ascii码，&#x为前缀，后跟字符的16进制的ascii码	"为&quot或&#34或&#x22 >为&gt <为&lt
16进制编码			对二进制数据进行16进制编码
base64	对二进制数据进行编码，用来将非ASCII字符的数据转换成ASCII字符	末尾经常出现=	大写字母A~Z,小写字母a~z,数字0~9以及"+","/"及用来填充的=
base32	对二进制数据进行编码，用来将非ASCII字符的数据转换成ASCII字符	末尾经常出现=	大写字母A~Z和数字2~7及用来填充的=
base16	对二进制数据进行编码，用来将非ASCII字符的数据转换成ASCII字符		数字0~9和字母A~F
unicode	对世界所有的字符编码	U+	用四个字节为每个字符进行编码，一般用16进制字符表示
utf8	把unicode字符进行编码，便于存储传输的编码方式	%	使用一至四个字节为每个字符编码
utf16	把unicode字符进行编码，便于存储传输的编码方式	%u	使用二或四个字节为每个字符编码
utf32	把unicode字符进行编码，便于存储传输的编码方式	%u	使用四个字节为每个字符编码
ascii码	对键盘的128个字符编码		使用7位二进制数来表示所有的大写和小写字母，数字0 到9、标点符号，以及在美式英语中使用的特殊控制字符
gbk	对中文字符编码		使用两个字节编码
bcd码	对二进制数据进行编码		用4位二进制数来表示一位十进制数中的0~9十个数码，有8421码，2421码，余3循环码等方式

数字信号编码

非归零编码NRE——高低电平分别用0和1表示

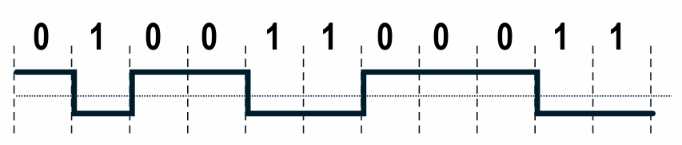
曼彻斯特编码——从高电平跳到低电平表示0，从低电平跳到高电平表示1

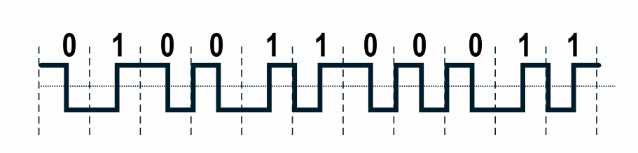
差分曼彻斯特编码——每一位中间有跳变，用来表示时钟，每一位开始时有跳变表示0，无表示1

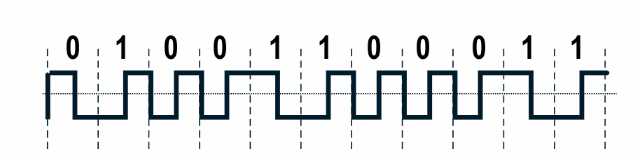
其它常见编码

霍夫曼编码

用于压缩，MP3编码等
简单的二元霍夫曼编码过程如下

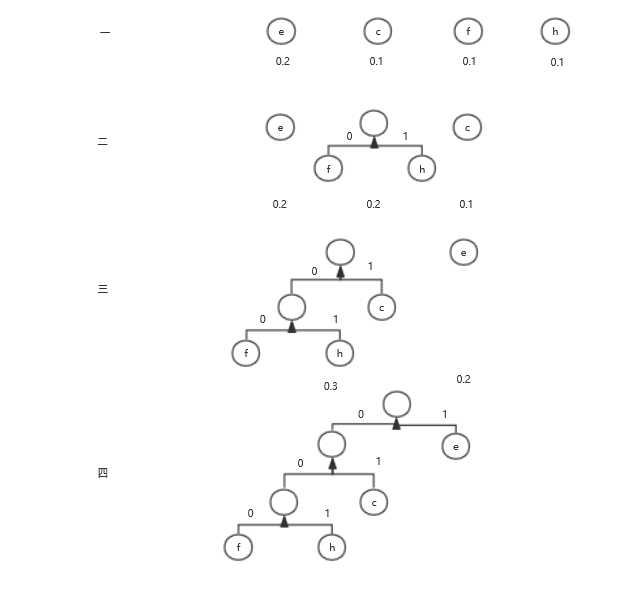
所以e的编码为1，c的编码为01，f的编码为000，h的编码为001

费诺编码

简单的二元费诺编码过程如下，不断分为概率相近的两组

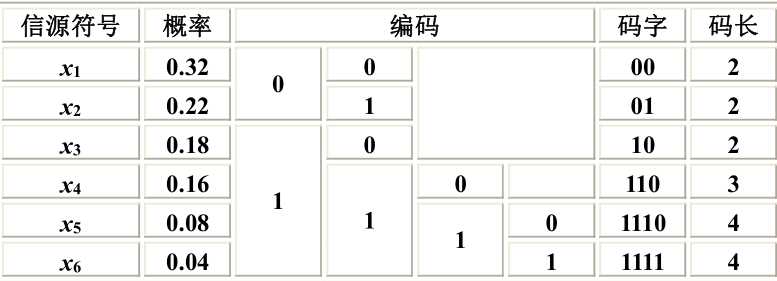
游程编码

用于卫星，医学图像等的编码，利用游程，例如图像像素为
3333
4333
2211
1111
灰度：3，4，3，2，1，1
长度：4，1，3，2，2，4
灰度用两位，长度用两位为1011，1100，1010，0101，0001，0011

差错控制码

奇偶校验码

增加一位奇（偶）校验位并一起存储或传送
比如：1111000中1位偶数添加一位为0表示1的位数为偶数，变为11110000，如果传输过程中发生了错误变为10110000，那么就可以知道有一位发生了错误。如果偶数个位错误，是无法发现的

循环冗余码crc

一个k位的二进制数据，左移r位，除以一个给定的r+1位的多项式相除，得到的r位余数就为校验码，拼到k位的二进制数后面
只要将接受到的数据和校验位用约定好的同样的生成多项式除，如果能除尽，表明没有发生错误（不一定，也有可能错误）；若除不尽，则表明某些数据位发生了错误
如信息码为1100，生成多项式为(x^{3}+x+1)
则1100平移3位1100000 除以1011，余数为010，拼在1100后面为1100010

海明校验码

能够纠正一位错误或者检测两位错误并纠一正位错误
设信息码为k位，校验码为r位，海明码为k＋r位
如果能够纠正一位错则应满足(2^{r}-1geq k+r)
如果能够发现两位错并纠正一位错则应满足(2^{r-1}geq k+r)
编码规律为

• 每个校验位(p_{i})放在海明码中位号为(2^{i-1})的位置
• 海明码的每一位（数据位和校验位）由多个校验位进行校验：被校验位的位号=校验位位号之和

例如求01101110的海明码，使其能纠正一位错误
一 确定校验位数
(2^{4}-1geq 8+4) 所以r为4
二 确定校验位所在位置
(2^{1-1})，(2^{2-1})，(2^{3-1})，(2^{4-1})所以海明码的1，2，4，8为校验位
三 分组

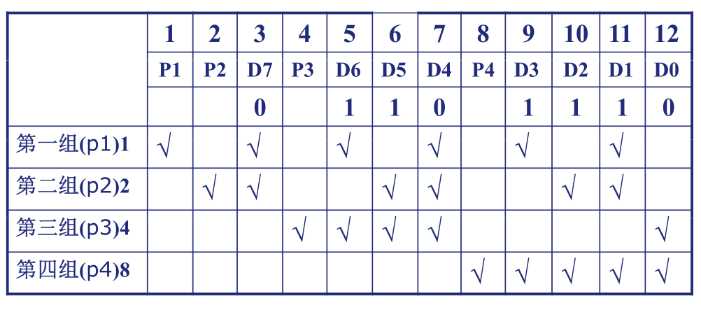
四 确定校验位
每一组除本身校验位外，所有位异或，如第一组为({D}_{7} oplus{D}_{6} oplus{D}_{4} oplus{D}_{3} oplus{D}_{1}={1})
四个校验码分别为1101，所以海明码为110011011110
五 校验
将每一组与本组的校验位异或，即({P}_{1} oplus{D}_{7} oplus{D}_{6} oplus{D}_{4} oplus{D}_{3} oplus{D}_{1})，如果校验位都为0，则无错,如果有错，校验位二进制编码即为出错位号，如，如果校验位为1010，则第第10位错，即({D}_{2})出错