十背包问题

Posted 2021-03-14 hbhszxyb

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了十背包问题相关的知识，希望对你有一定的参考价值。

12.1 `0/1` 背包问题

12.1.1 题目模型

有 N 件物品和一个容量为 V 的背包。第 i 件物品的体积是 v[i] ，价值是 cost[i]。求解将哪些物品装入背包可使价值总和最大。

12.1.2 基本思路

这是最基础的背包问题，特点是：每种物品仅有一件，可以选择放或不放。
用子问题定义状态：即 f[i][j] 表示前 i 件物品恰放入一个容量为 j 的背包可以获得的最大价值。则其状态转移方程便是：f[i][j]=max{f[i-1][j],f[i-1][j-v[i]]+cost[i]}
这个方程非常重要，基本上所有跟背包相关的问题的方程都是由它衍生出来的。所以有必要将它详细解释一下：
1. “将前 i 件物品放入容量为 j 的背包中”这个子问题，若只考虑第 i 件物品的策略（放或不放），那么就可以转化为一个只牵扯前 i-1 件物品的问题。
2. 如果不放第 i 件物品，那么问题就转化为“前 i-1 件物品放入容量为 j 的背包中”，价值为 f[i-1][j] ；
3. 如果放第 i 件物品，那么问题就转化为“前 i-1 件物品放入剩下的容量为 j-v[i] 的背包中”，此时能获得的最大价值就是 f[i-1][j-v[i]] + cost[i]。

12.1.3 例题

Description

给定 n 种物品和一个容量为 V 的背包，物品 i 的体积是 (v_i) ，其价值为 (c_i)。问：应该如何选择装入背包的物品，使得装入背包中的物品的总价值最大？

Input

第一行为两个正整数 n ，V ,表示有 n 件物品，背包容量为 V (( 1le nle 1000, 1le Vle 10000))

接下来n 行，每行两个正整数 (v_i, c_i) 表示第i 件物品的体积和价值。

Output

只有一行，为能放入背包的最大价值。

Sample Input
4 8
2 3
3 4
4 5
5 6
Sample Output
10

分析思路：
1. 定义 f[i][j] 表示前 i 件物品放入体积为 j 的背包中能获得的最大价值
2. 初始化时，i==0 || j==0 时f[i][j]=0，显然，没有物品，或背包为空时，价值为0 。
3. 我们从 1～n 枚举每一件物品，对当前的第 i 件物品进行分析：
  - 如果第 i 件物品的体积大于背包容量 j ，则当前的最优等价于前 i-1 件物品放入 j 的背包中,即f[i][j]=f[i-1][j]
  - 如果 v[i]<=j ，此时对第 i 件物品，我们有两种决策：
    1. 第 i 件物品放入容量为 j 的背包，则前 i-1 件物品能使用的背包容量只有 j-v[i] ，此时：f[i][j]=f[i-1][j-v[i]] + cost[i] 。
    2. 不放入第i 件物品，有可能让背包多放几件前 i-1 件物品，此时：f[i][j]=f[i-1][j] 。
    3. 对上面两种方案都有可能是最优，所以我们取其较大者,即:f[i][j]=max(f[i-1][j],f[i-1][j-v[i]]+cost[i])
4. 如图所示：
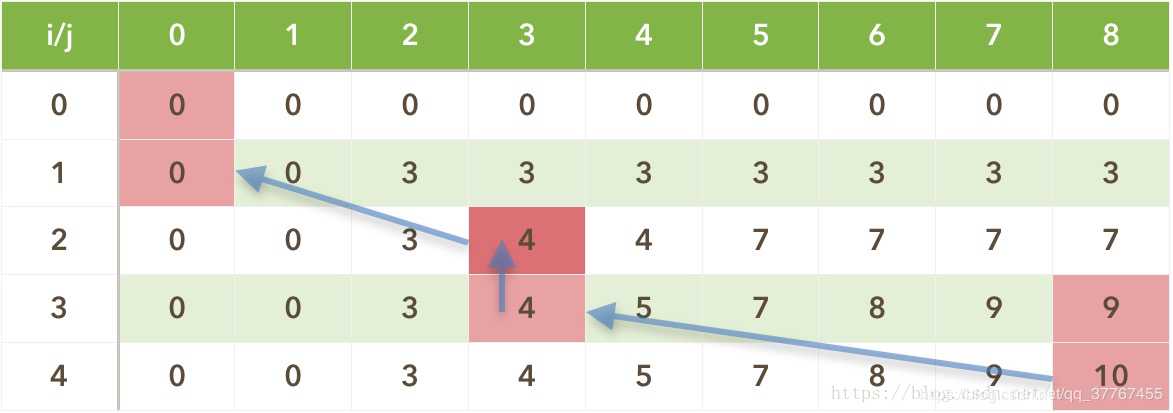
5. 代码实现：
```
#include <cstdio>
#include <cstring>
#include <algorithm>
const int maxn=1000+5,maxv=10000+5;
int v[maxn],c[maxn],f[maxn][maxv];
void Bag(int n,int V){
    for(int i=1;i<=n;++i)//依次枚举前i件物品
        for(int j=1;j<=V;++j)//从1~V枚举背包容量
            if(j<v[i])f[i][j]=f[i-1][j];//如果无法放进第i件物品
                        else f[i][j]=std::max(f[i-1][j],f[i-1][j-v[i]]+c[i]);
}
void Solve(){
    int n,V;scanf("%d%d",&n,&V);
    for(int i=1;i<=n;++i) scanf("%d%d",&v[i],&c[i]);
    Bag(n,V);
    printf("%d
",f[n][V]);
}
int main(){
    Solve();
    return 0;
}
```
6. 时间效率：O(n*V) ，内存：n * V

12.1.4 空间优化

以上方法的时间和空间复杂度均为 O(N*V) ，其中时间复杂度基本已经不能再优化了，但空间复杂度却可以优化到 O(V)。
先考虑上面讲的基本思路如何实现:
- 有一个主循环 i=1..N，每次算出来二维数组f[i][0..V] 的所有值。
- 那么，如果只用一个数组f[0..V] ，能不能保证第i 次循环结束后 f[j] 中表示的就是我们定义的状态f[i][j] 呢？
- f[i][j] 是由f[i-1][j] 和 f[i-1][j-v[i]] 两个子问题递推而来，能否保证在推 f[i][j] 时（也即在第 i次主循环中推 f[j]时）能够得到 f[i-1][j]和 f[i-1][j-v[i]] 的值呢？
- 事实上，这要求在每次主循环中我们以 j=V..0 的顺序推 f[j]，这样才能保证推 f[j] 时 f[j-v[i]] 保存的是状态f[i-1][j-v[i]]的值。

主要代码如下：

void Bag(int n,int V){
    for(int i=1;i<=n;++i)//依次枚举前i件物品
        for(int j=V;j>=v[i];--j)//从V~v[i]枚举背包容量
            f[j]=std::max(f[j],f[j-v[i]]+c[i]);
}

其中的 f[j]=max{f[j],f[j-v[i]]+cost[i]}一句恰就相当于我们的转移方程f[i][j]=max{f[i-1][j],f[i-1][j-v[i]]+cost[i]}，因为现在的 f[j-v[i]]就相当于原来的f[i-1][j-v[i]]。
如果将j的循环顺序从上面的逆序改成顺序的话，那么则成了 f[i][j] 由 f[i][j-v[i]] 推知，与本题意不符，但它却是另一个重要的背包问题最简捷的解决方案，故学习只用一维数组解 01背包问题是十分必要的。
时间效率：O(n*V) ，内存：V

12.1.5 `0/1` 背包初始化细节

我们看到的求最优解的背包问题题目中，事实上有两种不太相同的问法。
1. 题目要求“恰好装满背包”时的最优解
  - 初始化时除了f[0]为0其它f[1..V]均设为-∞，这样就可以保证最终得到的f[V]是一种恰好装满背包的最优解。
2. 题目并不有要求必须把背包装满，只要能装下即可。
  - 初始化时应该将f[0..V]全部设为0。
为什么呢？可以这样理解：
- 初始化的f数组事实上就是在没有任何物品可以放入背包时的合法状态。
- 如果要求背包恰好装满，那么此时只有容量为0的背包可能被价值为0的nothing“恰好装满”，其它容量的背包均没有合法的解，属于未定义的状态，它们的值就都应该是-∞了。
- 如果背包并非必须被装满，那么任何容量的背包都有一个合法解“什么都不装”，这个解的价值为0，所以初始时状态的值也就全部为0了。
- 这个小技巧完全可以推广到其它类型的背包问题，后面也就不再对进行状态转移之前的初始化进行讲解。

12.2 完全背包

12.2.1 题目模型

有 N 种物品和一个容量为 V 的背包，每种物品都有无限件可用，第 i 件物品的体积是 (v_i)，价值是 (c_i) 。求解将哪些物品装入背包可使价值总和最大。

12.2.2 基本思路

这个问题非常类似于01背包问题，所不同的是每种物品有无限件。
从每种物品的角度考虑，与它相关的策略已并非取或不取两种，而是有取0件、取1件、取2件……等。
按照解01背包时的思路，令 f[i][j] 表示前 i 种物品恰放入一个容量为 j 的背包的最大权值。
状态转移方程：f[i][j]=max{f[i-1][j-k*v[i]]+k*c[i]}(0<=k*v[i]<=j)

核心代码：

void Bag(int n,int V){//n件物品,背包荣咯昂为V
    for(int i=1;i<=n;++i){//枚举物品
        for(int k=0;k*v[i]<=V;++k)//取0~V/v[i]件i物品,k=0相当与不去第i件，此时f[i][j]=f[i-1][j]
            for(int j=k*v[i];j<=V;++j){//枚举容量 
                f[i][j]=std::max(f[i][j],f[i-1][j-k*v[i]]+k*c[i]);
        }
    }
}

时间效率：O(N*V*k)

12.2.3 优化

简单优化

若两件物品 i,j满足 v[i]<=v[j]且 c[i]>=c[j]，则将物品j去掉，不用考虑。
- 显然任何情况下都可将价值小费用高得j换成物美价廉的i，得到至少不会更差的方案。
- 对于随机生成的数据，这个方法往往会大大减少物品的件数，从而加快速度。
- 并不能改善最坏情况的复杂度，因为有可能特别设计的数据可以一件物品也去不掉。
将费用大于V的物品去掉。
使用类似计数排序的做法，计算出费用相同的物品中价值最高的是哪个，可以O(V+N)地完成这个优化。

注意：以上优化并不能从实质上提高时间效率，不过也是在数据比较大的情况下，特别是随机数据有很明显的提升。

二进制拆分优化

分拆方法：
- 把第i种物品拆成费用为 (v[i]*2^k) 、价值为 $ c [i]*2^k$ 的若干件物品，其中k满足 (v[i]*2^k<=V) 。
- 这是二进制的思想，因为不管最优策略选几件第 i 种物品，总可以表示成若干个(2^k) 件物品的和。
- 这样把每种物品拆成 (O(log(V/v[i])))件物品，是一个很大的改进。
- 注意：使用二进制拆分后不适合用二维数组表示，为啥呢？

核心代码实现：

void Bag(int n,int V){//n种物品,背包荣咯昂为V
    for(int i=1;i<=n;++i){//枚举物品
       for(int k=1;k*v[i]<=V;k<<=1)//枚举第i种物品个数
           for(int j=V;j>=k*v[i];--j)//枚举容量
                f[i][j]=std::max(f[i-1][j],f[i-1][j-k*v[i]]+k*c[i]);//此表达式有误
                            //因为此种定义方式使第i种物品只能取2^1,2^2……中的一种，而改为一维即正确
                            f[j]=std::max(f[j],f[j-k*v[i]]+k*c[i]);//正确，比较下两种写法的区别，自己思考        
        }
    }
}多重背包问题

O(VN)的算法

我们只需把01 背包的一维数组写法的容量枚举的顺序由倒序变为正序即可。
- 核心代码
```
void Bag(int n,int V){
    for(int i=1;i<=n;++i)//依次枚举前i件物品
        for(int j=v[i];j<=V;++j)//从v[i]~V枚举背包容量
            f[j]=std::max(f[j],f[j-v[i]]+c[i]);
}
```
  - 代码只有v的循环次序不同而已。为什么这样一改就可行呢？
  - 首先想想为什么0/1背包中要按照j=V..0的逆序来循环。这是因为要保证第i次循环中的状态f[i][j]是由状态f[i-1][j-v[i]]递推而来。换句话说，这正是为了保证每件物品只选一次，保证在考虑“选入第i件物品”这件策略时，依据的是一个绝无已经选入第 i件物品的子结果f[i-1][j-v[i]]。
  - 完全背包的特点恰是每种物品可选无限件，所以在考虑“加选一件第i种物品”这种策略时，却正需要一个可能已选入第i种物品的子结果f[i][j-v[i]]，所以就可以并且必须采用j=0..V的顺序循环。这就是这个简单的程序为何成立的道理。
  - 这个算法也可以以另外的思路得出。例如，基本思路中的状态转移方程可以等价地变形成这种形式：
    
    f[i][j]=max{f[i-1][j],f[i][j-v[i]]+c[i]}
    - f[i-1][j] ：表示第i 种物品一件也不取
    - f[i][j-v[i]] 表示前i种物品，包括第i种已取若干的基础上再取一件第i种物品

12.3 多重背包问题

12.3.1 题目模型

有 N 种物品和一个容量为 V 的背包，第i种物品最多有cnt[i]件可用，第 i 件物品的体积是 (v_i)，价值是 (c_i) 。求解将哪些物品装入背包可使价值总和最大。

12.3.2 基本思路

和完全背包问题很类似。基本的方程只需将完全背包问题的方程略微一改即可
因为对于第i种物品有cnt[i]+1种策略：取0件，取1件……取cnt[i]件。
令 f[i][j]表示前i种物品恰放入一个容量为j的背包的最大权值，则有状态转移方程：
- f[i][j]=max{f[i-1][j-k*v[i]]+k*c[i]} (0<=k<=n[i])
- 时间复杂度：(O(V*sum_1^ncnt[i]))。

12.3.3 二进制拆分优化

将第i种物品分成若干件物品，其中每件物品有一个系数
这些系数分别为(2^0,2^1,2^2,...,2^{k-1},cnt[i]-2^k+1)，且k是满足(cnt[i]ge 2^k)的最大整数。
- 例如，如果cnt[i]为13，就将这种物品分成系数分别为1,2,4,6的四件物品。
- 1,2,4,6 能组合成1~13 之间的任何一个数。
这样就将第i种物品分成了O(log cnt[i])种物品，将原问题转化为了复杂度为 (O(V*sum_1^n log ctn[i]))的01背包问题，是很大的改进。

核心代码实现：

void Bag(int n,int V){
    for(int i=1;i<=n;++i){//枚举物品
        int tot=0;//统计第i种物品已经分解出tot件
        for(int k=1;tot+k<=cnt[i] && k*v[i]<=V;k<<=1){//要分解出k件第i物品
            tot+=k;
            for(int j=V;j>=k*v[i];--j)//对分解出来的k件i物品做01背包
                f[j]=std::max(f[j],f[j-k*v[i]]+k*c[i]);
        }
        int x=cnt[i]-tot;//二进制分解剩下部分，x有可能很大
        if(x)//剩下部分不为0，再跑一次01背包
            for(int j=V;j>=x*v[i];--j)
                f[j]=std::max(f[j],f[j-x*v[i]]+x*c[i]);
    }
}

12.3.4 O(VN)的算法

多重背包问题同样有O(VN)的算法。这个算法基于基本算法的状态转移方程，但应用单调队列的方法使每个状态的值可以以均摊O(1)的时间求解。
由于用单调队列优化的DP 目前对大家有一定难度，以后再讲

12.4 混合三种背包问题

有的物品只可以取一次（01背包），有的物品可以取无限次（完全背包），有的物品可以取的次数有一个上限（多重背包）。应该怎么求解呢？

显然，枚举每件物品时根据物品的件数，选择相应的背包。

代码实现

#include <cstdio>
#include <cstring>
#include <algorithm>
const int maxn=1000+5,maxv=10000+5,Inf=0x7fffffff;
int f[maxv],v[maxn],c[maxn],cnt[maxn];
void multi_bag(int i,int V){//多重背包
    int tot=0;//统计第i种物品已经分解出tot件
    for(int k=1;tot+k<=cnt[i] && k*v[i]<=V;k<<=1){//要分解出k件第i物品
        tot+=k;
        for(int j=V;j>=k*v[i];--j)//对分解出来的k件i物品做01背包
            f[j]=std::max(f[j],f[j-k*v[i]]+k*c[i]);
        }
    int x=cnt[i]-tot;//二进制分解剩下部分
    if(x)//剩下部分不为0，再跑一次01背包
        for(int j=V;j>=x*v[i];--j)
            f[j]=std::max(f[j],f[j-x*v[i]]+x*c[i]);
    }
void zero_bag(int i,int V){//01背包
    for(int j=V;j>=v[i];--j)
        f[j]=std::max(f[j],f[j-v[i]]+c[i]);
    }
void complete_bag(int i,int V){//完全背包
    for(int j=v[i];j<=V;++j)
        f[j]=std::max(f[j],f[j-v[i]]+c[i]);
    }
void Solve(){
    int n,V;scanf("%d%d",&V,&n);
    for(int i=1;i<=n;++i){
        scanf("%d%d%d",&cnt[i],&v[i],&c[i]);
        if(cnt[i]==1) zero_bag(i,V);
        else if(cnt[i]>=V/v[i]) complete_bag(i,V);
        else multi_bag(i,V);
    }
    printf("%d
",f[V]);
}
int main(){
    Solve();
    return 0;
}

12.5 二维费用的背包问题

12.5.1 题目模型

对于每件物品，具有两种不同的费用；选择这件物品必须同时付出这两种代价；对于每种代价都有一个可付出的最大值（背包容量）。问怎样选择物品可以得到最大的价值。设这两种代价分别为代价1和代价2，第i件物品所需的两种代价分别为a[i]和b[i]。两种代价可付出的最大值（两种背包容量）分别为V和U。物品的价值为c[i]。

12.5.2 基本思路

费用加了一维，只需状态也加一维即可。
设f[i][v][u]表示前i件物品付出两种代价分别为 v 和 u 时可获得的最大价值。状态转移方程就是：

f[i][v][u]=max{f[i-1][v][u],f[i-1][v-a[i]][u-b[i]]+w[i]}
当前状态只跟上一行状态相关，所以我们可以省略第一维：
1. 当每件物品只可以取一次时变量 v 和 u 采用逆序的循环。
2. 当物品有无数件时采用顺序的循环。
3. 当物品有有限件时，拆分物品。

12.6 分组的背包问题

12.6.1 题目模型

有N 件物品和一个容量为 V 的背包。第 i 件物品的体积v[i]，价值是c[i]。这些物品被划分为若干组，每组中的物品互相冲突，最多选一件。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。

12.6.2 基本思路

这个问题变成了每组物品有两种策略：
1. 选择本组的某一件
2. 一件都不选
也就是说设f[k][v] 表示前 k 组物品用容量为 v的背包装，能取得的最大权值，则有：

f[k][V]=max{f[k-1][V],f[k-1][V-v[i]]+c[i]} 物品i属于第k组
使用一维数组的伪代码如下：
```
for 所有的组k
    for v=V..0
        for 所有的i属于组k
            f[v]=max{f[v],f[v-v[i]]+c[i]}
```
- 注意这里的三层循环的顺序。for v=V..0 这一层循环必须在for 所有的i属于组k 之外。这样才能保证每一组内的物品最多只有一个会被添加到背包中。

12.7 例题

12.7.1 HDU - 2546 饭卡

题目大意

电子科大本部食堂的饭卡有一种很诡异的设计，即在购买之前判断余额。如果购买一个商品之前，卡上的剩余金额大于或等于5元，就一定可以购买成功（即使购买后卡上余额为负），否则无法购买（即使金额足够）。所以大家都希望尽量使卡上的余额最少。
某天，食堂中有 (n) 种菜出售，每种菜可购买一次。已知每种菜的价格以及卡上的余额，问最少可使卡上的余额为多少。

样例

样例输入 1

10
1 2 3 2 1 1 2 3 2 1
50

样例输出 1

样例 1 说明

有 10 种菜，结果自己算吧

样例输入2

1
50
5

样例输出2

-45

样例 2 说明

只有一种菜，价格为 (50)，卡上余额 (5) 元，此时买这个菜，剩余 (-45)。

分析

此题不难，先自己想想实际生活中，如果卡里余额不小于 5 块钱，而且什么都能买，但是只能买一件，你会怎么买？
很显然，如果钱足够，所有东西都买；如果不够，肯定要用尽量用 (money-5) 这么多钱买东西，最后剩下的钱买最贵的，非常贪婪。
怎么实现最后买最贵的？显然把物品排序，最贵的放最后，因为我们跑背包是按照物品逐个处理的，因此，可以把前 (n-1) 个物品跑 01 背包，看看 (money) 这么多钱最多能花多少，假设花了 (x)，再计算 (money-x-price[n]) 即可。
证明稍后再加

部分代码

暂时不想写了

12.7.2 POJ - 2184 Cow Exhibition 题解

题目大意

有 (N(N le 100)) 头奶牛，没有头奶牛有两个属性 (s_i) 和 (f_i)，两个范围均为 ([-1000, 1000])。
从中挑选若干头牛，(TS = sum s[choose], TF = sum f[choose])。
求在保证 (TS) 和 (TF) 均为非负数的前提下，(TS+TF)最大值。

样例

有 5 头牛，下面分别是每头牛的两个属性
5
-5 7
8 -6
6 -3
2 1
-8 -5
选择第 1、3、4 三头牛为最优解
虽然加上 2 号，总和会更大，但是 TF 会变成负数，不合法

分析

首先从问题入手，先搞特殊情况：如果两个属性均为负数，果断舍弃，因为它一直在做负贡献
一个物品有两个属性，会很自然想到二维费用背包，每个物品的价值为两个属性的和，也就是两种费用的和，这样定义其实意义并不大，而且时间复杂度为 (O(N*S*F))，最大会到 (10^8)，应该会超时。
由于价值直接是两者的和，所以我们没必要单独构造一个价值，而是把其中的一维改成价值即可，即用 (S_i) 当作费用，(F_i) 当作价值，最后扫一遍求最大和就可以了
另外一个棘手的问题就是负数的问题：
- 对于价值来说，正负都不影响，直接正常跑背包求最大值即可
- 当费用为非负数时，没什么影响，正常跑 01 背包求最值，背包容积倒叙处理即可，(f[j] = max {f[j], f[j-s_i]+f_i})。
- 当费用为负数时，如果直接用上述的式子，(j-S_i > j)，而背包容积倒叙的话，(f[j-s_i]) 会先于 (f[j]) 被计算。如果直接这样写，会变成完全背包的样子，不妥。因此只需要把容积改成正序循环即可。
- 由于下标不能为负数，我们可以将 (0) 点改成 (100*1000)，这样的话，即使所有物品的费用都为负数，下标也依旧处在合法的范围内。此时背包的容积也就相应变成了 ([0~200000])。
- 注意跑背包的时候的边界即可
- 最后统计时，当费用不小于 (100000) 时才表示 (TS) 的和为非负数，找到所有价值为非负数的那些，最后求两者和的最大值即可。

部分代码

心情好的时候再加

12.7.3 HDU - 3591 Coins 题解

题目大意

有 (N) 种不同面值的硬币，分别给出每种硬币的面值 (v_i) 和数量 (c_i)。同时，售货员每种硬币数量都是无限的，用来找零。
要买价格为 (T) 的商品，求在交易中最少使用的硬币的个数（指的是交易中给售货员的硬币个数与找回的硬币个数之和）。
个数最多不能超过 (20000)，如果不能实现，输出 (-1)；否则输出此次交易中使用的最少的硬币个数。

样例

有 (3) 种硬币，面值分别为 (5, 25 50)，个数分别为 (5, 2, 1)，要买 (70) 的商品，不存在给小费的情况下，最少的硬币个数为 (3)。
自己使用 (25) 和 (50) 各一个，找回一个面值为 (5) 的硬币。

分析

这个问题在普通背包的基础上，加入了找零的情况，很显然，如果自己拥有的硬币，即使恰好能购买商品，也不一定是使用硬币最少的，例如样例中，自己恰好买的话，使用硬币数为 (4)，即 (5) 的 (4) 个，(50) 的 (1) 个，共 (5) 个。
既然要求最后支出 (pay_{T+i}) 与找回 (back_i) 的硬币总和最少，即求 (min{pay_{T+i} + back_i})。
对于样例来说，我们还需要考虑：
- 付 (75) 使用的个数 + 找 (5) 的个数
- 付 (80) 使用的个数 + 找 (10) 的个数
- ...
- 其中有些数是达不到的，因此需要加判断。
我们可以对自己的硬币跑多重背包，最大容量为 (20000)，(pay_i) 表示恰好付钱为 (i) 的时候所需要的最好硬币个数；对售货员跑完全背包，(back_i) 表示找回 (i) 所需要的的最少硬币个数。最后扫一遍，最小化 (min{pay_{T+i} + back_i})。

部分代码

还没顾上写;

以上是关于十背包问题的主要内容，如果未能解决你的问题，请参考以下文章

十：贪心算法-背包问题

dp（未完成）

算法系列学习[kuangbin带你飞]专题十二基础DP1 F - Piggy-Bank 完全背包问题

如何完成活动？（喷气背包导航）

防止导航到同一个片段

SpringCloud系列十一：SpringCloudStream（SpringCloudStream 简介创建消息生产者创建消息消费者自定义消息通道分组与持久化设置 RoutingKey）(代码片段

十背包问题

12.1 0/1 背包问题

12.1.1 题目模型

12.1.2 基本思路

12.1.3 例题

12.1.4 空间优化

12.1.5 0/1 背包初始化细节

12.2 完全背包

12.2.1 题目模型

12.2.2 基本思路

12.2.3 优化

12.3 多重背包问题

12.3.1 题目模型

12.3.2 基本思路

12.3.3 二进制拆分优化

12.3.4 O(VN)的算法

12.4 混合三种背包问题

12.5 二维费用的背包问题

12.5.1 题目模型

12.5.2 基本思路

12.6 分组的背包问题

12.6.1 题目模型

12.6.2 基本思路

12.7 例题

12.7.1 HDU - 2546 饭卡

题目大意

样例

样例输入 1

样例输出 1

样例 1 说明

样例输入2

样例输出2

样例 2 说明

分析

部分代码

12.7.2 POJ - 2184 Cow Exhibition 题解

题目大意

样例

分析

部分代码

12.7.3 HDU - 3591 Coins 题解

题目大意

样例

分析

部分代码

12.1 `0/1` 背包问题

12.1.5 `0/1` 背包初始化细节