Codeforces Round #614 (Div. 2) A-E简要题解

Posted 2021-03-13 aaronchang

链接：https://codeforces.com/contest/1293

 

A. ConneR and the A.R.C. Markland-N

题意：略

思路：上下枚举1000次扫一遍，比较一下上下最近的房间

AC代码：

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<algorithm>
 4 #include<cmath>
 5 #include<map>
 6 #include<utility>
 7 #include<string>
 8 #include<vector>
 9 #include<cstring>
10 #include<iostream>
11 #include<vector>
12 #include<algorithm>
13 #include<cmath>
14 #include<cstring>
15 #include<queue>
16 #include<cstdio>
17 #include<unordered_map>
18 using namespace std;
19 const int maxn=1e5;
20 typedef long long ll;
21 
22 int main()
23 {
24     int t;
25     cin >> t;
26     while(t--)
27     {
28         map<int,int> v;
29         int n,s,k;
30         scanf("%d%d%d",&n,&s,&k);
31         int x;
32         for(int i=1; i<=k; i++)
33         {
34 
35             scanf("%d",&x);
36             v[x]++;
37         }
38         int l,r;
39         l=r=s;
40         if(!v[s])
41             cout << 0 << endl;
42         else
43         {
44             while(v[l]&&v[r])
45             {
46                 if(l-1>=1)
47                     l--;
48                 if(r+1<=n)
49                     r++;
50 
51             }
52             if(!v[r]&&!v[l])
53             {
54                 cout << min(s-l,r-s) << endl;
55             }
56             else if(!v[r]&&v[l])
57             {
58                 cout << r-s<< endl;
59             }
60             else if(v[r]&&!v[l])
61                 cout << s-l << endl;
62         }
63     }
64     return 0;
65 }

 

B. JOE is on TV!

 

题意：略

思路：比较简单，推结论 max （n） = i/n+(i-1)/n + ...n/n

AC代码：

 1 #include<iostream>
 2 #include<vector>
 3 #include<algorithm>
 4 #include<cmath>
 5 #include<cstring>
 6 #include<queue>
 7 #include<cstdio>
 8 #include<unordered_map>
 9 using namespace std;
10 typedef long long ll;
11 int main(){
12     int t;
13     float ans = 0;
14     scanf("%d",&t);
15     float i = 1;
16     while(i<=t){
17         ans+=(1/i);
18         i+=1;
19     }
20     printf("%.12lf",ans);
21     return 0;
22 }

 

 

C. NEKO‘s Maze Game

题意：有一个2×n的网格迷宫，网格可以翻动，由正常区域和堵塞区域切换，问从（1，1）能否到（2，n）

思路：一个网格如果翻动，如果这个网格是在第二列，那么这个网格可以和其左上角、正上方、右上角构成堵塞，这样算是三个“堵塞贡献”，如果位于第一列翻动由正常区域变成堵塞，那么这个网格可以和左下角、正下方、右下方的网格构成堵塞区域，这样也是三个贡献，每次放置网格就计算上这些贡献，换回正常的时候就减去，如果总的贡献是0，那么就可以到达（2，n）

AC代码：

 1 #include<iostream>
 2 #include<vector>
 3 #include<algorithm>
 4 #include<cmath>
 5 #include<cstring>
 6 #include<queue>
 7 #include<cstdio>
 8 #include<unordered_map>
 9 using namespace std;
10 typedef long long ll;
11 const int maxn = 1e5+15;
12 int grid[2][maxn];
13 int can[maxn];
14 int main(){
15     int n,q;
16     int cnt = 0;
17     scanf("%d%d",&n,&q);
18     while(q--){
19         int x,y;
20         scanf("%d%d",&x,&y);
21         x = x - 1;
22         if((grid[0][y]+grid[1][y]) == 2){
23             cnt--;
24         }
25         if(grid[x][y]+grid[(x+1)%2][y-1] == 2){
26             cnt--;
27         }
28         if(grid[x][y]+grid[(x+1)%2][y+1] == 2){
29             cnt--;
30         }
31         grid[x][y] = (grid[x][y]+1)%2;
32         if((grid[0][y]+grid[1][y]) == 2 ){
33             cnt++; 
34         }
35         if(grid[x][y]+grid[(x+1)%2][y-1] == 2 ){
36             cnt++; 
37         }
38         if(grid[x][y]+grid[(x+1)%2][y+1] == 2 ){
39             cnt++; 
40         }
41         if(cnt == 0){
42             printf("YES
");
43         }
44         else printf("NO
");
45     }
46     return 0;
47 }

 

D. Aroma‘s Search

题意：二维平面上有若干个点，第i个点的坐标(xi,yi)满足xi=xi-1*ax+bx,yi=y-1*ay+by，已知 ax,bx,ay,by,x0,y0 以及初始位置(xs,ys)，每秒钟可以往上下左右走1个单位，则在t秒内最多可以走到多少个点

思路：所有点之间的曼哈顿距离是乘指数级别增长的，不能到了一个点之后再回到初始点，也不能从距离最近的点开始出发去枚举。考虑到数据范围，其实点的极限数量大概在60多，所以可以构造一个暴力的算法去枚举。最佳的方案是先从起点到其中一个点，再从这个点向下面的点移动，因为向上比向下距离远，如果下方所有的点都可以到达，再往上走，这样是最佳的方案。所有需要枚举起点到每一个点，再从该点先向下方移动再向上移动

AC代码：

 

 1     #include<bits/stdc++.h>
 2     using namespace std;
 3     typedef long long ll;
 4     ll x0,y0,ax,ay,bx,by,xs,ys,t;
 5     vector<pair<ll,ll> > v;
 6     ll solve(int x){
 7         ll remain = t;
 8         remain -= abs(v[x].first-xs)+abs(v[x].second-ys);
 9         if(remain<0) return 0;
10         ll res = 1;
11         int last = x;
12         for(int i = x-1;i>=0;i--){
13             ll can = abs(v[i].first-v[last].first)+abs(v[i].second-v[last].second);//先向下方的点移动
14             if(remain-can<0) break;
15             res++;
16             remain-=can; 
17             last = i;
18         }
19         for(int i = x+1;i<v.size();i++){
20             ll can = abs(v[i].first-v[last].first)+abs(v[i].second-v[last].second);//如果还有时间剩余向上方点移动
21             if(remain-can<0) break;
22             res++;
23             remain-=can; 
24             last = i;    
25         }
26         return res;
27     }
28     int main(){
29         cin>>x0>>y0>>ax>>ay>>bx>>by;
30         cin>>xs>>ys>>t;
31         ll curx = x0,cury = y0;
32         while(1){
33             ll disX = abs(curx-xs);
34             ll disY = abs(cury-ys);
35             if(curx>xs && cury>ys && disX+disY > t) break;//如果移动到该点就超过了t秒，break
36             v.push_back({curx,cury});
37             curx = ax*curx+bx;
38             cury = ay*cury+by;
39         }
40         ll ans = 0;
41         for(int i = 0;i<v.size();i++){
42             ans = max(ans,solve(i));//枚举到每个点
43         }
44         cout<<ans;
45         return 0;
46     }

 

 

 

 

E. Xenon‘s Attack on the Gangs

题意：给出一颗树，树上随机分配边权值，不存在权值相同的两条边，定义mex（u，v）表示点u到点v经过边的边权集合S中没有出现的最小非负整数，求S = ∑mex（u，v） （1<=u<=v<=n）的最大值。

思路：这道题没有太明白，看官方题解首先要推出一个组合公式，问题转化为求一条边的贡献，对u到v的路径进行dp，枚举u到v的每一条路径的贡献。

放个官方题解吧

 

 

 

 

 

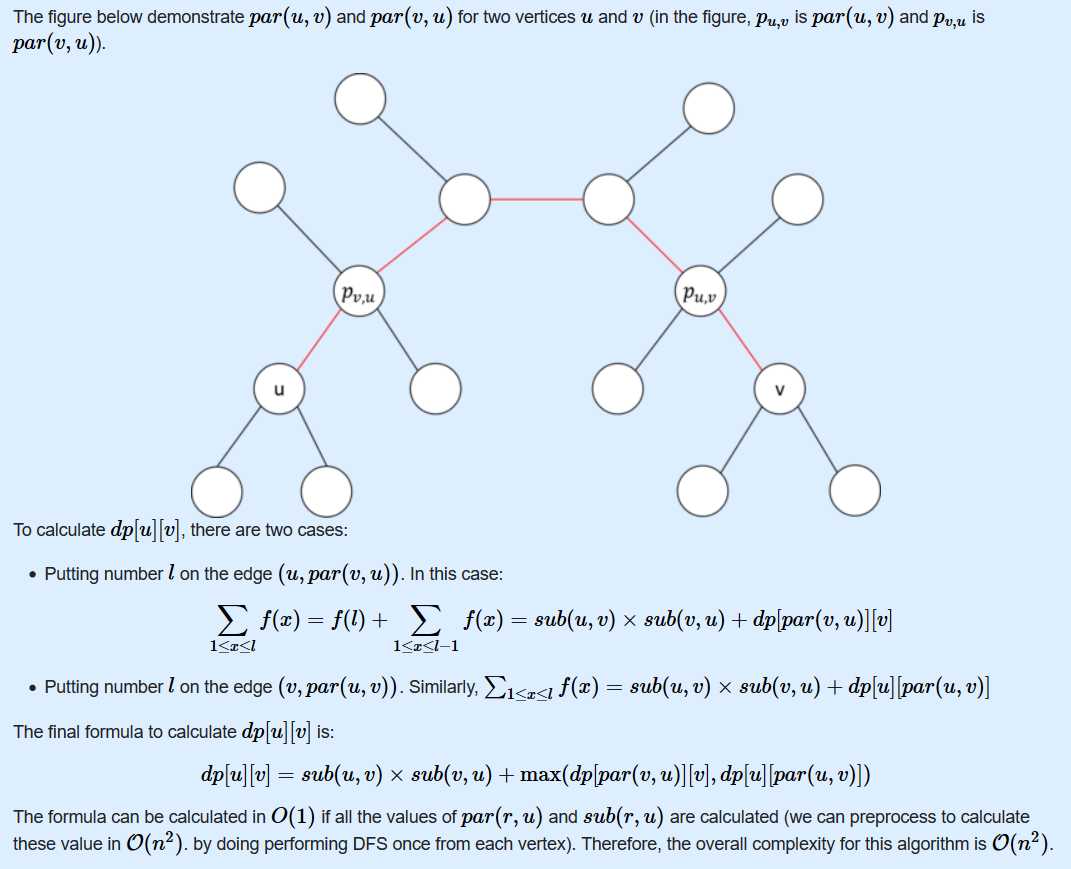
AC代码：

 1 #include<bits/stdc++.h> 
 2 using namespace std;
 3 const int maxn = 3005;
 4 typedef long long ll;
 5 int fa[maxn][maxn],sub[maxn][maxn];
 6 ll dp[maxn][maxn];
 7 vector<int> G[maxn]; 
 8 int n,root;
 9 int dfs(int cur,int father){
10     sub[root][cur] = 1;
11     for(int i = 0;i<G[cur].size();i++){
12         if(G[cur][i]!=father){
13             fa[root][G[cur][i]] = cur;
14             sub[root][cur]+=dfs(G[cur][i],cur);
15         }
16     }
17     return sub[root][cur];
18 }
19 ll getDp(int u,int v){
20     if(u == v) return 0;
21     if(dp[u][v] ) return dp[u][v];
22     return dp[u][v] = sub[u][v]*sub[v][u] + max(getDp(fa[v][u],v),getDp(fa[u][v],u));
23 }
24 int main(){
25     scanf("%d",&n);
26     for(int i = 1;i<n;i++) {
27         int u,v;
28         cin>>u>>v;
29         G[u].push_back(v),G[v].push_back(u);  
30     }
31     for(int i = 1;i<=n;i++){
32         root = i;
33         dfs(i,-1);
34     }
35     ll res = 0;
36     for(int i = 1;i<=n;i++){
37         for(int j = 1;j<=n;j++){
38             res = max(res,getDp(i,j));
39         }
40     }
41     printf("%lld",res);
42     return 0;
43 }