线性表的简单应用

Posted 2021-03-13 jlnu-cn

线性表

•线性表是我们最先接触，也是最简单的一种数据结构的表现方式。

•线性表分为顺序表和链表，也就是顺序存储结构和链式存储结构的两种表现形式。

 

1.顺序表

　　•顺序表是在计算机内存中以数组的形式保存的线性表，线性表的顺序存储是指用一组地址连续的存储单元依次存储线性表中的各个元素、使得线性表中在逻辑结构上相邻的数据元素存储在相邻的物理存储单元中，即通过数据元素物理存储的相邻关系来反映数据元素之间逻辑上的相邻关系，采用顺序存储结构的线性表通常称为顺序表。顺序表是将表中的结点依次存放在计算机内存中一组地址连续的存储单元中。

 

1.定义顺序表结构体:

#define MAXN 100100
typedef struct list
{
    int data[MAXN]; //存储空间
    int last; //当前最后一个元素的下标(last+1表示当前表的长度)
    int maxsize; //最大元素个数(表的最大长度)
}squenlist;

 

2.初始化结构体

void init(squenlist *L,int maxsize)
{
    L->last = -1; //将last赋值为-1为了方便访问数组下标
    L->maxsize = maxsize; //获取表的最大长度
}

 

3.建表

定义了结构体并且初始化了之后，就要开始建表了，建立顺序表的过程可以简化为一个给数组赋值的过程

int create_list(squenlist *L,int x)
{
    if(L->last >= L->maxsize - 1) //如果需要存储的元素个数超过最大表长则不插入该元素并返回0
    {
        printf("The list is full!,cant‘t insert element %d
",x);
        return 0;
    }
    L->last++; //下标右移
    L->data[L->last] = x; //给当前存储空间赋值
    return 1;
}

 

4.顺序表的操作(index--需要做操作的位置，此处位置为数组下标位置，x--需要操作的元素值)

1)判断下标是否符合要求

如果给定的下标在表外则返回0

int judge_index_over(squenlist *L,int index)
{
    if(index > L->last || index < -1)
        return 0;
    else
        return 1;
}

2）增添元素

int insert_element_index(squenlist *L,int index,int x)
{
    if(!judge_index_over(L,index))
        return 0;
    L->last++;
    for(int i = L->last ;i >= index; i--)
        L->data[i+1] = L->data[i];
    L->data[index] = x;
    return 1;
}

3）删除元素

int delete_element_index(squenlist *L,int index)
{
    int remember_element;
    if(!judge_index_over(L,index))
        return 0;
    remember_element = L->data[index]; //记录已删除的元素
    for(int i = index; i < L->last; i++)
        L->data[i] = L->data[i+1];
    L->data[L->last] = NULL; 
    L->last--; //下标左移
    return remember_element; //返回删除元素的值
}

4）修改元素

int change_element_index(squenlist *L,int index,int x)
{
    if(!judge_index_over(L,index))
        return 0;
    L->data[index] = x;
    return 1;
}

5）查询元素

int query_element_index(squenlist *L,int index)
{
    if(!judge_index_over(L,index))
        return 0;
    return L->data[index]; //返回查询位置的元素值
}

6）打印顺序表

void print_list(squenlist *L)
{
    for(int i = 0; i <= L->last; i++)
        printf("%d ",L->data[i]);
    putchar(‘
‘);
}

7）获取当前顺序表长度

 

int get_length(squenlist *L)
{
    return L->last + 1;
}

 

 

2.链表

　　•链表分为很多种，有单向链表，双向链表，环形链表，二叉链表等，这里我们先介绍最简单的单向链表。

　　•单链表是一种链式存取的数据结构，用一组地址任意的存储单元存放线性表中的数据元素。链表中的数据是以结点来表示的，每个结点的构成：元素(数据元素的映象) +指针(指示后继元素存储位置)，元素就是存储数据的存储单元，指针就是连接每个结点的地址数据。

 

/*
单链表:
单向链表,有表头与表尾
例1:head|next -> 1|next -> 2|next ->   3|next -> 4|next -> NULL(带头节点的单链表)
例2:head -> 1|next -> 2|next ->   3|next -> 4|next -> NULL(不带头节点的单链表)
链表相较于顺序表具有便于删改的特点,即链表的删改仅需涉及到待删改元素或位置附近元素的修改;
若需要测试没有在主函数中调用的函数请自行调用函数测试;
*/

1.定义结点：

结点由两部分组成：

1).数据域；

2).指针域；

typedef struct node//申请结点
{
    int data;//数据域
    struct node *next;//指针域
}linklist;

 

2.建立链表

1）头插法

原理:

 

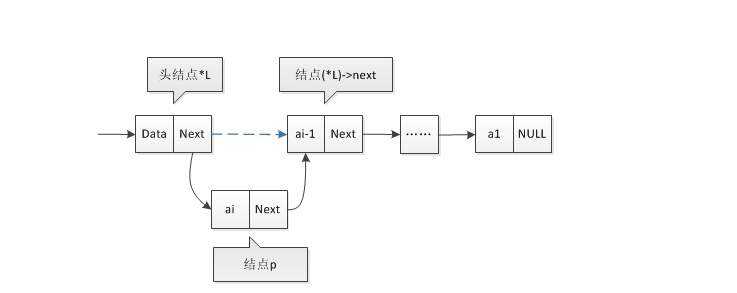
代码实现：

linklist *create_list_front()//头插法建表
{
    int n;
    linklist *s, *head;
    head = (linklist*)malloc(sizeof(linklist));
    head->next = NULL;
    scanf("%d", &n);
    while (n != -1)
    {
        s = (linklist*)malloc(sizeof(linklist));
        s->data = n;
        s->next = head->next;//修改头节点
        head->next = s;
        scanf("%d", &n);
    }
    return head;
}

 2）尾插法

 原理:

 

代码实现:

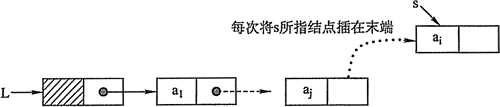
linklist *create_list_rear(linklist *head)//尾插法建表
{
    linklist *s, *r;
    int n;
    head = (linklist*)malloc(sizeof(linklist));//头节点的申请
    head->next = NULL;//头节点next指针置空
    r = head;
    scanf("%d", &n);
    while (n != -1)
    {
        s = (linklist*)malloc(sizeof(linklist));//申请新结点
        s->data = n;//数据域赋值
        r->next = s;//修改尾结点
        r = s;
        scanf("%d", &n);
    }
    r->next = NULL;//表尾置空,若不置空则会发生之后遍历链表循环无法跳出的情况
    return head;
}

 

3.链表的操作(下面的操作讲解会以代码注释的形式呈现)

1）插入元素

/*
链表元素添加的原理:
head-> 1|next -> 2|next -> 3|next -> 4|next -> NULL;
若index = 2,n = 5;
                p               q
                |               |
                /              /
则有head|next -> 1|next   ->     2|next -> 3|next -> 4|next -> NULL
                               >
                      > 5|next /
                       /                       |
                       s
数据域为1的节点next指针 指向 数据域为5的节点的数据域,数据域为5的节点的next指针 指向 数据域为2的节点的数据域
申请p,q,s三个指针来完成该操作
先让q指向p->next所指的区域,即 q = p->next;
再让p->next指向s所指的区域,即 p->next = s;
最后让s->next指向q所指的区域,即 s->next = q;
*/
linklist *add_node(linklist *head, int n, int index) //在链表任意位置添加元素
{
    linklist *p, *s, *q;
    p = head->next;
    if (index == 1)//头节点之后的第一个节点单独处理
    {
        s = (linklist*)malloc(sizeof(linklist));
        s->data = n;
        head->next = s;
        s->next = p;
    }
    else
    {
        while (index - 2)//将指针指到要添加的位置
        {
            p = p->next;
            index--;
        }
        s = (linklist*)malloc(sizeof(linklist));
        s->data = n;
        q = p->next;
        p->next = s;
        s->next = q;
    }
    return head;
}

2）删除元素

/*
链表元素删除的原理:
head-> 1|next -> 2|next -> 3|next -> 4|next -> NULL;
若index = 2,n = 2;
则有
             p        q
             |        |
             /       /
head|next -> 1|next -> 2|next ->   3|next -> 4|next -> NULL
                                 >
            \\____________________/
数据域为1的节点的next指针 指向 数据域为3的节点(数据域为2的节点的下一个节点)的数据域
申请p,q两个指针来完成本操作
q指针 指向 p指针所指向节点的next指针所指向的区域,即 q = p->next;
再让p->next 指向 q->next所指的区域,即 p->next = q->next;
*/
linklist *delete_node(linklist *head, int n)//删除链表任意位置的元素
{
    linklist *p, *q;
    p = head->next;
    if (p->data == n)
    {
        q = head->next->next;
        head->next = q;
    }
    else
    {
        p = head->next;
        while (p->next->data != n)
        {
            p = p->next;
        }
        q = p->next;
        p->next = q->next;
    }
    return head;
}

3）查询元素

/*
查找元素的原理:
与打印链表相同,都是遍历链表,之后返回元素值
*/
int search_data(linklist *head, int index)//查找元素值,并返回
{
    linklist *p;
    p = head->next;
    while (index - 1)
    {
        index--;
        p = p->next;
    }
    return p->data;
}


/*
查找元素下标的原理:
与打印链表相同,都是遍历链表,之后返回下标
*/
int search_index(linklist *head, int n)//查询指定元素的值并返回位置,若为空则返回0
{
    int index = 0;
    linklist *p;
    int flag = 0;
    p = head->next;
    while (p != NULL)
    {
        index++;
        if (p->data == n)
        {
            flag = 1;
            return index;
        }
        p = p->next;
    }
    if (flag == 0)
        return 0;
}

4）查询区间和与链表当前长度

/*
查询区间和原理:
遍历链表,返回区间和
*/
int search_sum_range(int l, int r, linklist *head)//查询链表区间和  l-r:查询区间
{
    linklist *p;
    int sum = 0;
    p = head->next;
    int i = l, j = r;
    while (i - 1)//先找到左区间元素的位置
    {
        i--;
        p = p->next;
    }
    while (j - l + 1)//将右区间元素之前的元素(包括右区间的元素)求和
    {
        sum += p->data;
        p = p->next;
        j--;
    }
    return sum;
}

/*
查询链表长度原理:
遍历链表,返回length
*/
int get_list_length(linklist *head)
{
    int length = 0;
    linklist *p;
    p = head->next;
    while (p != NULL)
    {
        length++;
        p = p->next;
    }
    return length;
}

5）两个链表的连接

/*
连接单链表原理:
例:
head1|next -> 1|next -> 2|next -> 3|next -> 4|next -> NULL
                                                                                                 >
                                    head2|next -> 5|next -> 6|next -> 7|next -> 8|NULL
*/
linklist* link_linklist(linklist *head1, linklist *head2)//连接两个单链表
{
    linklist *p;
    p = head1;
    while (p->next != NULL)
    {
        p = p->next;
    }
    p->next = head2->next;
    return head1;
}

总结：

•顺序表的优点：

　　查询元素便利，空间利用率高；

•顺序表的缺点：

　　增删元素复杂，需要直接开辟一整块空间。

•链表的优点：

　　增删元素容易，随时开辟存储空间，操作方便；

•链表的缺点：

　　空间利用率低，查询元素复杂。