计算复杂度理论的入门内容

Posted ryedii-blog

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了计算复杂度理论的入门内容相关的知识，希望对你有一定的参考价值。

  • 决定性问题（Decision problem）：指在某些形式系统回答是或否的问题。例如，“给定两个数字 (x) 与 (y)，(x) 是否可以整除 (y) ？”

在计算复杂度的领域中，分类可决定问题的依据在于此问题有多难被解决，难是以解决问题最有效率的算法的计算资源为依据的。

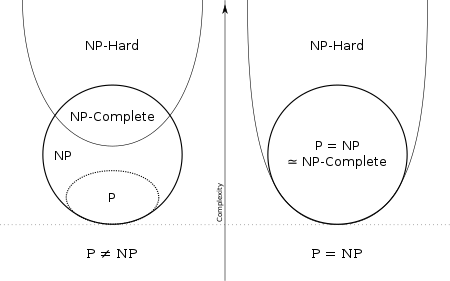
  • P 问题（多项式问题，Polynomial problem）：在多项式复杂度内可以被解决的问题。

  • NP 问题（非决定性多项式问题，Non-deterministic Polynomial problem）：在多项式复杂度内可以被验证其正确性的问题。

[ ext{P}subseteq ext{NP} ]

  • P/NP 问题：世纪难题 ( ext{P}overset{?}{=} ext{NP})。

  • 归约：指讲某个计算问题转换为另一个问题的过程。

  • NP 困难（NP-hardness，NP-hardness）：如果所有 NP 问题都可以多项式复杂度归约到某个问题，则称该问题为 NP 困难。

  • NP 完全（NP 完备，NPC，NP-Complete）：如果所有 NP 问题都可以多项式复杂度归约到某个 NP 问题，则称该问题为 NP 完全。

[ ext{NPC}= ext{NP }cap ext{ NP-hard} ]