GSS3/1 - Can you answer these queries 3/1

Posted 2021-03-13 shatianming

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了GSS3/1 - Can you answer these queries 3/1相关的知识，希望对你有一定的参考价值。

这个题集好好,那天我做一下(开个大坑?)

嘛,题目难的是查询,这里就只讲查询了

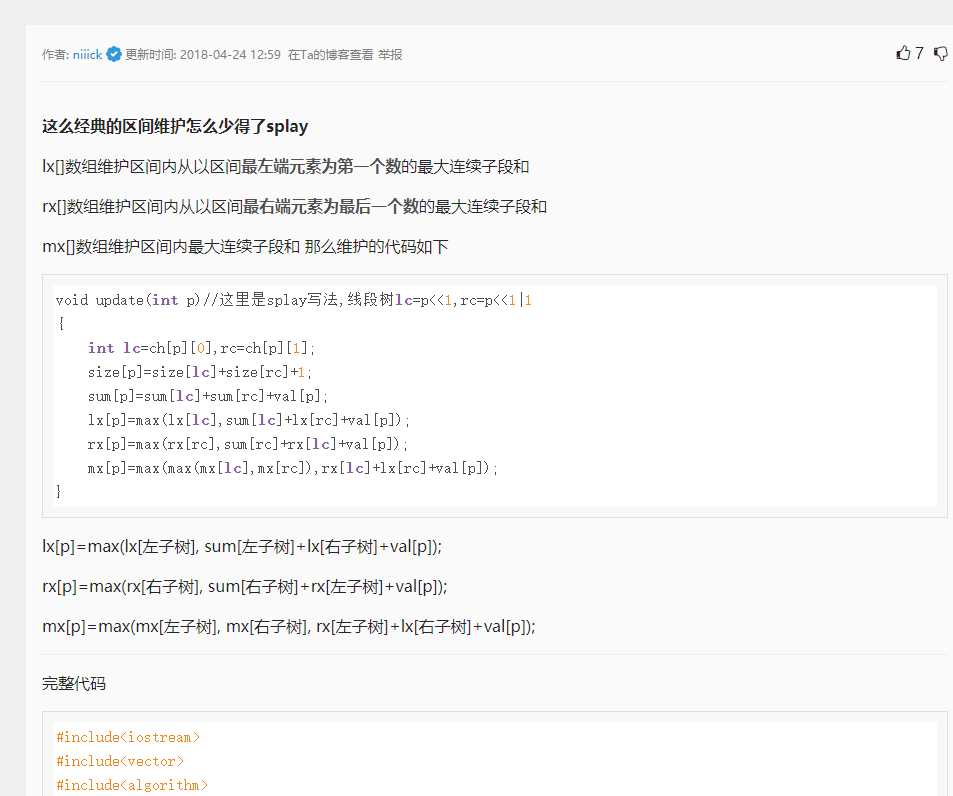
根据题解,我们用线段树维护3个东西

lx:表示从lx走,所能在给定区间里面的最大值

rx:参考上面

mx:表示在给定区间中间截取一段所能取到的最大值

那么对于题目给定的查询区间(假设其为L,R)

我们用线段树去遍历这个区间(访问,,,,,比较好点吧)

如果L---R刚好对应线段树的一个区间,那么直接返回我们的mx就好了(正确性显然)

相对的,存在不对应区间的情况

考虑合并答案

对于我们线段树的每次操作相当于把一段区间一分为二

那么我们可以借用线段树的操作,维护一个在线段树维护范围内的又在L---R的部分答案

然后就可以合并

对于这个部分答案,很好维护

只要将遍历所有L---R内的线段树局部节点就可以解决

#include<bits/stdc++.h>
#define MAXN 400000
using namespace std;

int n,q,date[MAXN];
int tp,mb1,mb2;
struct node{
    int sum;
    int lx,rx,mx;
}t[MAXN*4];

int up(int now){
    t[now].sum = t[now*2].sum+t[now*2+1].sum;
    t[now].lx = max(t[now*2].lx,t[now*2].sum+t[now*2+1].lx);
    t[now].rx = max(t[now*2+1].rx,t[now*2].rx+t[now*2+1].sum);
    t[now].mx = max(max(t[now*2].mx,t[now*2+1].mx),t[now*2].rx+t[now*2+1].lx);
}

int build(int ll,int rr,int now){
    if(ll==rr){
        t[now].lx = t[now].rx = t[now].mx = t[now].sum = date[ll];
        return 0;
    }
    int mid = (ll+rr)>>1;
    build(ll,mid,now*2);
    build(mid+1,rr,now*2+1);
    up(now);
}

int change(int now,int l,int r,int x,int y){//在x上改成y 
    int mid = (l+r)>>1;
    if(r<x||l>x)return 0;
    if(x==l&&x==r){
        t[now].lx = t[now].rx = t[now].mx = t[now].sum = y;
        return 0;
    }
    change(now*2+1,mid+1,r,x,y);
    change(now*2,l,mid,x,y);
    
    up(now);
    
}

node found(int ml,int mr,int now,int l,int r){
    if(l>=ml&&r<=mr){
        return t[now];        
    }     
    int mid = (l+r)>>1;
    node ans,a,b;
    if(mid<ml)return found(ml,mr,now*2+1,mid+1,r);
    if(mid>=mr)return found(ml,mr,now*2,l,mid); 
    else{
    a = found(ml,mr,now*2,l,mid);
    b = found(ml,mr,now*2+1,mid+1,r);
    ans.sum = a.sum+b.sum;
    ans.lx = max(a.lx,a.sum+b.lx);
    ans.rx = max(a.rx+b.sum,b.rx);
    ans.mx = max(a.rx+b.lx,max(a.mx,b.mx));
    return ans;    
    }
}

int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>date[i];
    }
    build(1,n,1);
    cin>>q;
    for(int i=1;i<=q;i++){
        cin>>tp>>mb1>>mb2;
        if(tp==1){
            node p=found(mb1,mb2,1,1,n);
        cout<<p.mx<<endl;
        }
        else{
            change(1,1,n,mb1,mb2);
        }
        
    }
}