# 伸展树 Splay

Posted 2021-03-11 sstealer

伸展树 Splay

维基百科上称为伸展树，但是国内好像一般叫平衡树，是众多平衡树中比较优秀的一种。

平衡树左旋右旋不会影响中序遍历顺序。

一棵平衡树的中序遍历顺序是值递增排序的，相当于从小到大到大排了一次序。

平衡树的作用：

平衡树其实就是一棵二叉搜索树，set和map都是平衡树实现。

一棵二叉搜索树理论深度是(O(log(n)))，但是当二叉树退化成链表的时候，深度就变成了(O(n))，很多(O(log))级别从操作会退化成(O(n))线性级别的操作。平衡树就是在不改变二叉搜索树中序遍历顺序的前提下，将树进行多次旋转操作，将树的左右子树尽量平衡，也就是将深度尽量的降低。

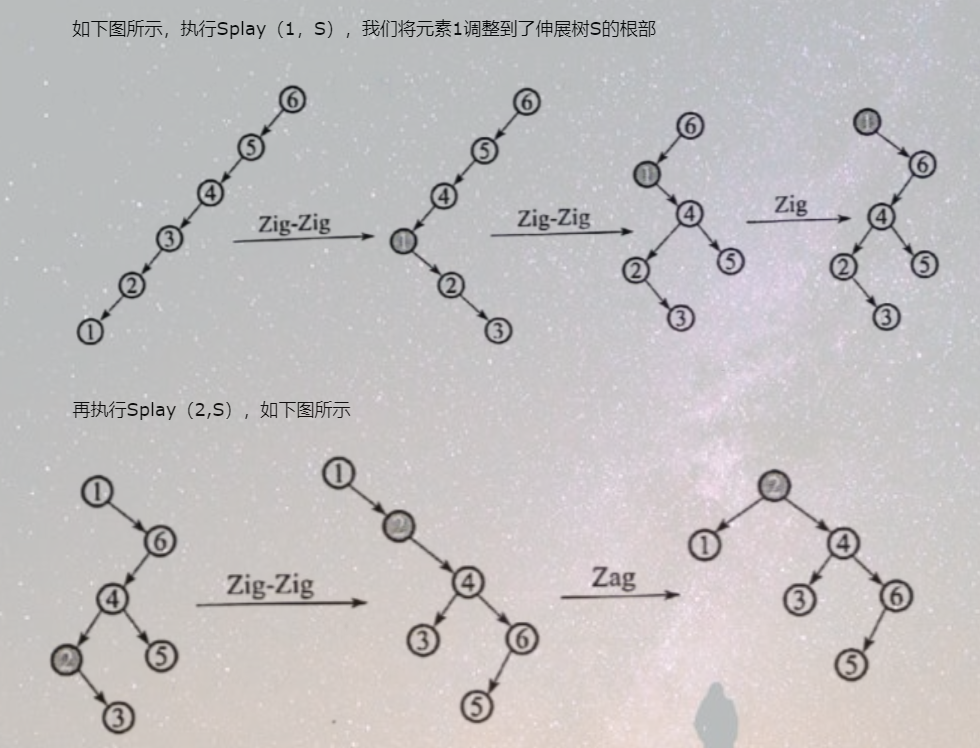
平衡树主要实现的操作：

1. 插入数值x。
2. 删除数值x(若有多个相同的数，应只删除一个)。
3. 查询数值x的排名(若有多个相同的数，应输出最小的排名)。
4. 查询排名为x的数值。
5. 求数值x的前驱(前驱定义为小于x的最大的数)。
6. 求数值x的后继(后继定义为大于x的最小的数)。

set和map可以实现一些操作，但是受到会自动去重的限制，所以平衡树相当于手写的set或map。

空间复杂度(O(n))，每种操作((log n))

模板题：

实现一种数据结构，提供以下操作：

1. 插入数值x。
2. 删除数值x(若有多个相同的数，应只删除一个)。
3. 查询数值x的排名(若有多个相同的数，应输出最小的排名)。
4. 查询排名为x的数值。
5. 求数值x的前驱(前驱定义为小于x的最大的数)。
6. 求数值x的后继(后继定义为大于x的最小的数)

注意： 数据保证查询的结果一定存在。

#include <bits/stdc++.h>
using namespace std;
const int N=201000;

struct splay_tree
{
    int ff,cnt,ch[2],val,size;
    //ff为父节点，cnt为当前节点值的个数（x=2，这个值可能有两个）
    //val为当前节点的值，size为当前节点左子树存了多少个值
} t[N];

int root,tot;
void pushup(int x)//从子节点更新父节点的信息
{
    //左子树+右子树+本身多少个,cnt记录重复个数.
    t[x].size=t[t[x].ch[0]].size+t[t[x].ch[1]].size+t[x].cnt;
}

//x是要旋转的节点，这个函数只是将旋转规则实现了一下
//根据x，x父节点，x祖父节点的位置，对x进行一次旋转
void rotate(int x)
{
    int y=t[x].ff;
    int z=t[y].ff;
    int k=(t[y].ch[1]==x);
    t[z].ch[(t[z].ch[1]==y)]=x;
    t[x].ff=z;
    t[y].ch[k]=t[x].ch[k^1];
    t[t[x].ch[k^1]].ff=y;
    t[x].ch[k^1]=y;
    t[y].ff=x;
    pushup(y);pushup(x);
}

void splay(int x,int s)//将x旋转为s的儿子，如果s是0则旋转到根
{
    while(t[x].ff!=s)
    {
        int y=t[x].ff,z=t[y].ff;
        if (z!=s)
            (t[z].ch[0]==y)^(t[y].ch[0]==x)?rotate(x):rotate(y);
        rotate(x);
    }
    if (s==0)root=x;//如果s是0，则将根节点更新为x
}
void find(int x)//查找x的位置，并将其旋转到根节点
{
    int u=root;
    if (!u)return ;//树空
    while(t[u].ch[x>t[u].val] && x!=t[u].val)
        u=t[u].ch[x>t[u].val];
    splay(u,0);//把当前位置旋转到根节点
}

void insert(int x)//插入x
{
    int u=root,ff=0;
    while(u && t[u].val!=x)
    {
        ff=u;
        u=t[u].ch[x>t[u].val];
    }
    if (u)
        t[u].cnt++;
    else
    {
        u=++tot;
        if (ff)
            t[ff].ch[x>t[ff].val]=u;
        t[u].ch[0]=t[u].ch[1]=0;
        t[tot].ff=ff;
        t[tot].val=x;
        t[tot].cnt=1;
        t[tot].size=1;
    }
    splay(u,0);
}
int Next(int x,int f)//查找x的前驱(f=0)或者后继(f=1)
{
    find(x);
    int u=root;
    if (t[u].val>x && f)
        return u;
    if (t[u].val<x && !f)
        return u;
    u=t[u].ch[f];
    while(t[u].ch[f^1])
        u=t[u].ch[f^1];
    return u;
}
void Delete(int x)//删除x
{
    int last=Next(x,0);
    int Net=Next(x,1);
    splay(last,0);
    splay(Net,last);
    int del=t[Net].ch[0];
    if (t[del].cnt>1)
    {
        t[del].cnt--;
        splay(del,0);
    }
    else
        t[Net].ch[0]=0;
}
int kth(int x)//查找排名为x的数
{
    int u=root;
    while(t[u].size<x)
        return 0;
    while(1)
    {
        int y=t[u].ch[0];
        if (x>t[y].size+t[u].cnt)
        {
            x-=t[y].size+t[u].cnt;
            u=t[u].ch[1];
        }
        else if (t[y].size>=x)
            u=y;
        else
            return t[u].val;
    }
}
int main()
{
    int n;
    scanf("%d",&n);
    insert(1e9);//加入哨兵
    insert(-1e9);//加入哨兵
    while(n--)
    {
        int opt,x;
        scanf("%d%d",&opt,&x);
        if (opt==1)
            insert(x);
        if (opt==2)
            Delete(x);
        if (opt==3)
        {
            find(x);//找到x，并将x旋转到根节点
            printf("%d
",t[t[root].ch[0]].size);//因为有哨兵的存在，根节点的左边一定有-inf的哨兵在，所以不用t[t[root].ch[0]].size+1
        }
        if (opt==4)
            printf("%d
",kth(x+1));
        if (opt==5)
            printf("%d
",t[Next(x,0)].val);
        if (opt==6)
            printf("%d
",t[Next(x,1)].val);
    }
    return 0;
}
/*
插入数值x。
删除数值x(若有多个相同的数，应只删除一个)。
查询数值x的排名(若有多个相同的数，应输出最小的排名)。
查询排名为x的数值。
求数值x的前驱(前驱定义为小于x的最大的数)。
求数值x的后继(后继定义为大于x的最小的数)。
*/