算法学习——trie树求最大异或对

Posted 2021-03-11 flydoggie

 

 

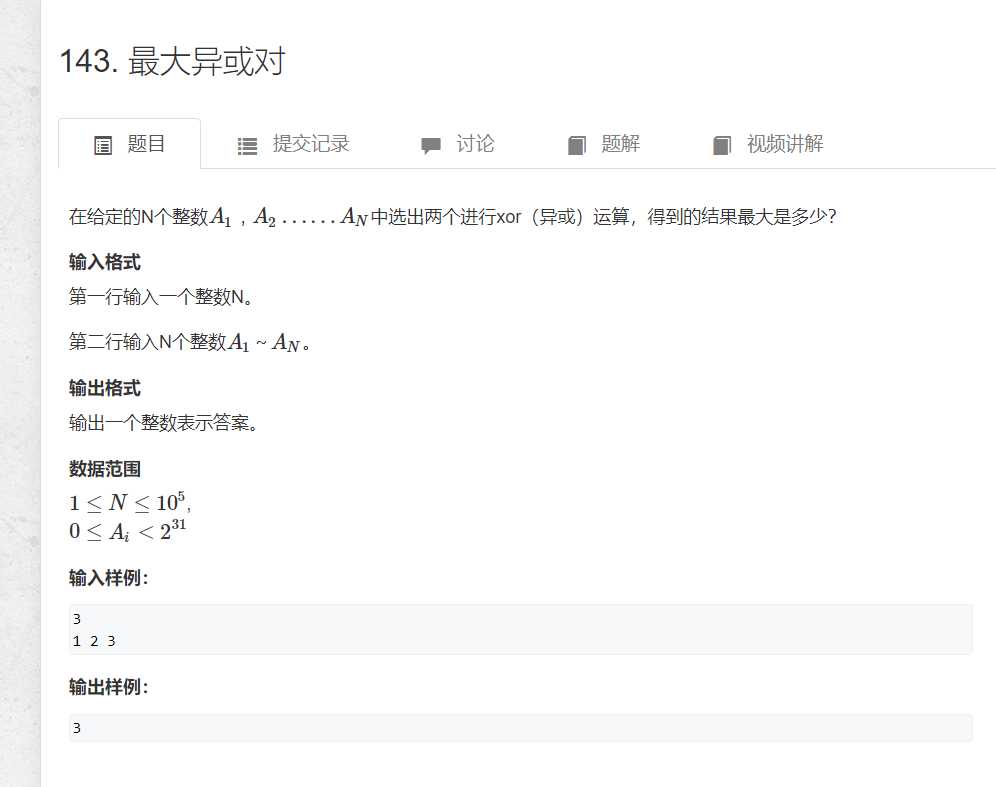
这道题目很难想到是字典树,如果不是放在字典树单元的话.
简单来说,一个整数,是可以转化成为一个32位的二进制数,而也就可以变成长度为32位的二进制字符串.
既然如此的话,根据二进制异或的原理：不同得1，否则得0，假如想让这个数字最大，我们就需要使得这个数的二进制表示中从左往右尽可能的取到1，也就是尽量的使得1最多。

那么我们可以这么做：

每一次检索的时候,我们都走与当前AiAi这一位相反的位置走,也就是让Xor值最大,如果说没有路可以走的话,那么就走相同的路.

详情见代码：

#include<iostream>
using namespace std;

const int N = 100010;

int s[N*32][2],idx;
int cnt[N*32];
int t[N],res;

void insert(int x){
    int p = 0;
    for(int i = 30;i >= 0 ;i -- ){
        //取x从二进制上右往左第i位上的数
        int n = x >> i & 1;
        //先判断该子节点是否存在
        if(!s[p][n]){
            //若不存在的话就创建
            s[p][n] = ++ idx;
            p = s[p][n];
        }else{
            //若存在的话就继续
            p = s[p][n];
        }
    }
}

int query(int x){
    int res = 0;
    int p = 0;
    for(int i = 30; i>=0 ; i --){
        //取x从二进制上右往左第i位上的数
        int n = x >> i & 1;
        //先判断是否存在和n不同的子节点
        if(s[p][!n]){
            //若存在则选则此节点；并且将对应位置二进制异或的值加到结果里
            res += 1 << i;
            p = s[p][!n];
        }else{
            //若不存在则选择存在的子节点
            p = s[p][n];
        }
    }
    return res;
}


int main(){
    int n;
    cin>>n;
    for(int i = 0 ; i < n ;i ++ ){
        cin>>t[i];
        insert(t[i]);
    } 
    for(int i = 0 ; i < n ; i ++){
        res = max(res,query(t[i]));
    }
    cout<<res<<endl;
    
    
    
    return 0;
}