11-pagerank 图机器学习之PageRank

Posted 2021-03-11 combfish

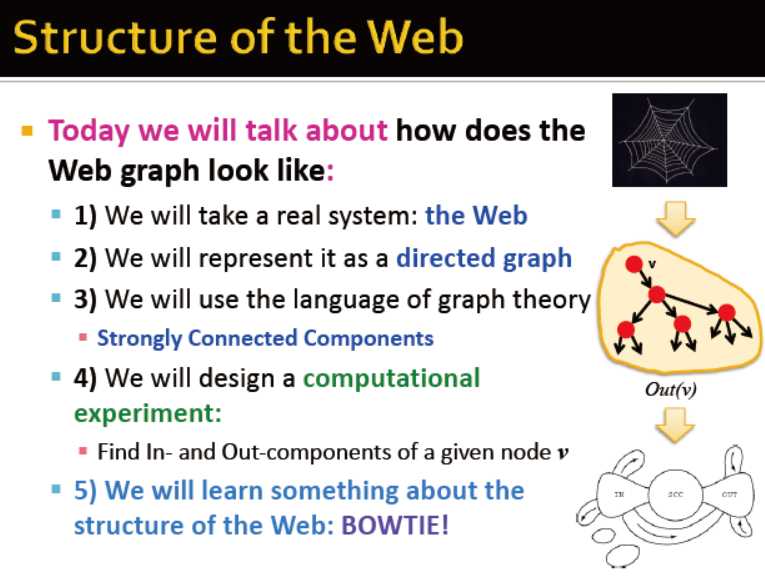
pagerank：链接分析

---

如同图谱的网络

每个网页相互链接，是一个有向图，强连通分量

设计一个计算十堰，找到给定节点的输入与输出成分（？）

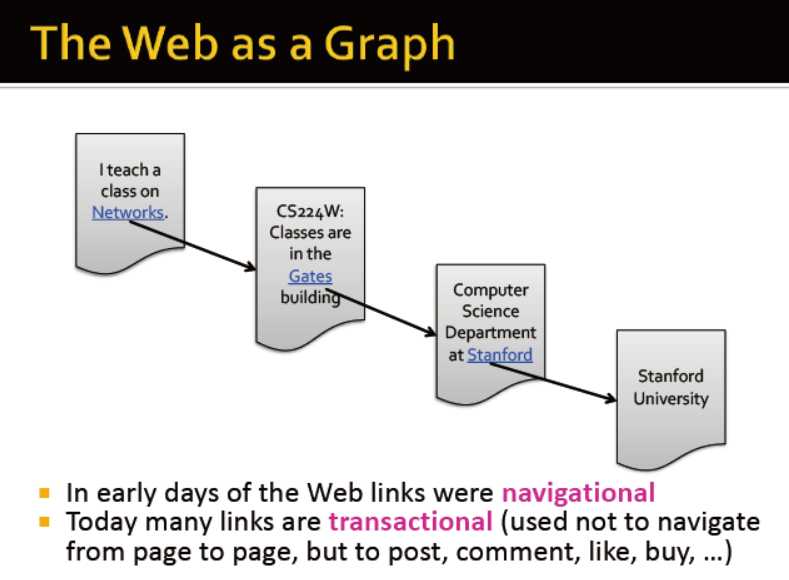
节点：网页

边：超链接

次要问题：动态页面如何解决？暗网——无法直接进入的网页

网页的现状：不一定通过导航链接，而通过交易事务（？），例如邮件，评论，评论，点赞，购买等

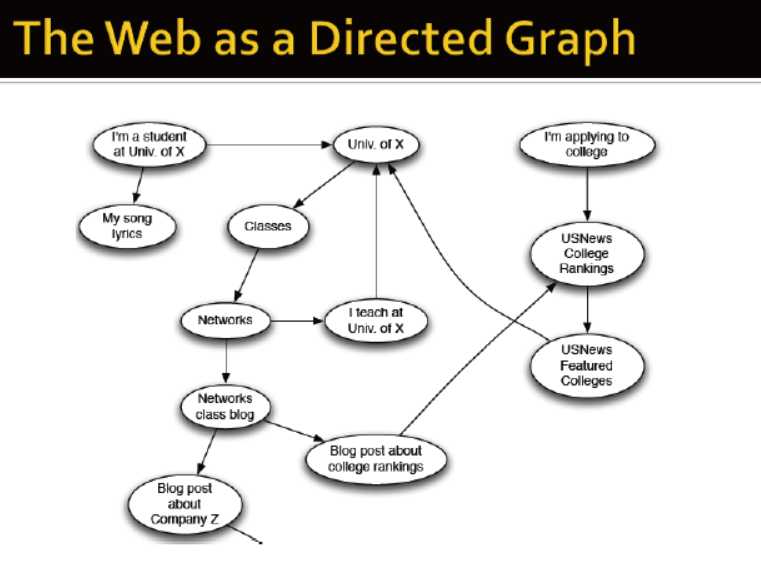
是一个有向图

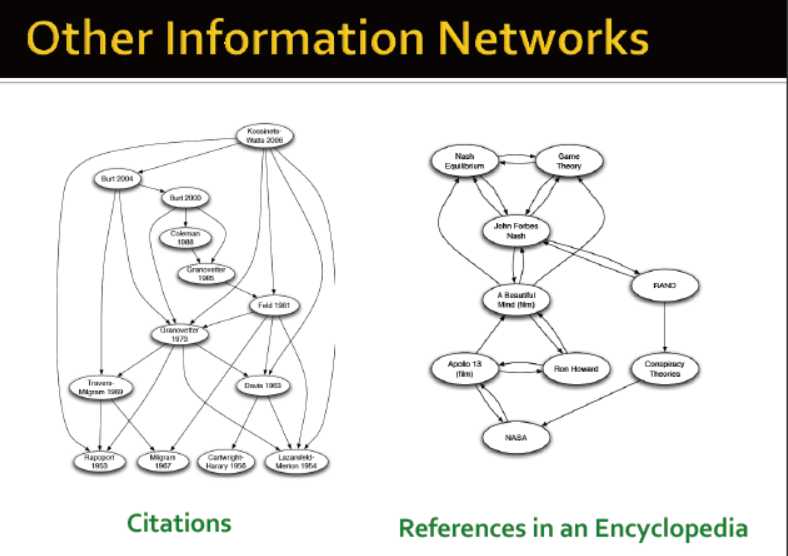
其他类型的信息网络：如引用网络，百科中的引用

In(v) OUT(v)的定义：通过输入或输出关系可以接触节点v的节点集合

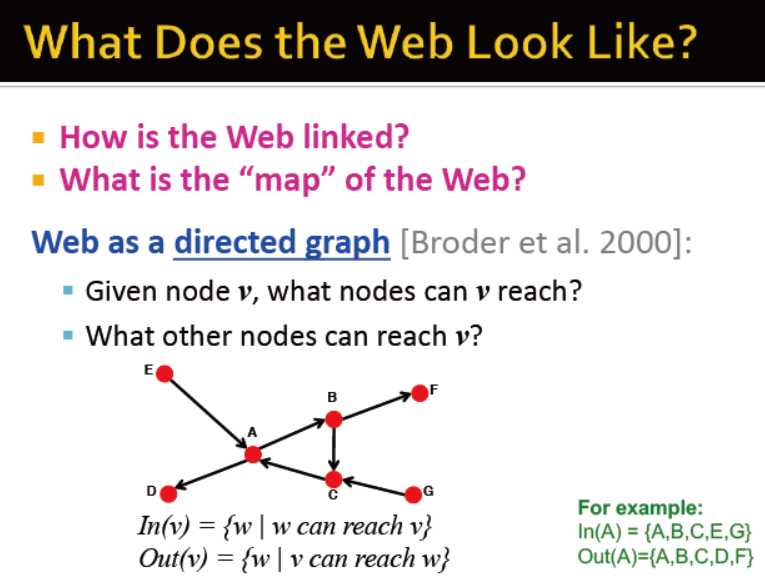
有向图的推理

有向图的两种类型：

1）强连接（任意两节点间相连）

2）邮箱无环图

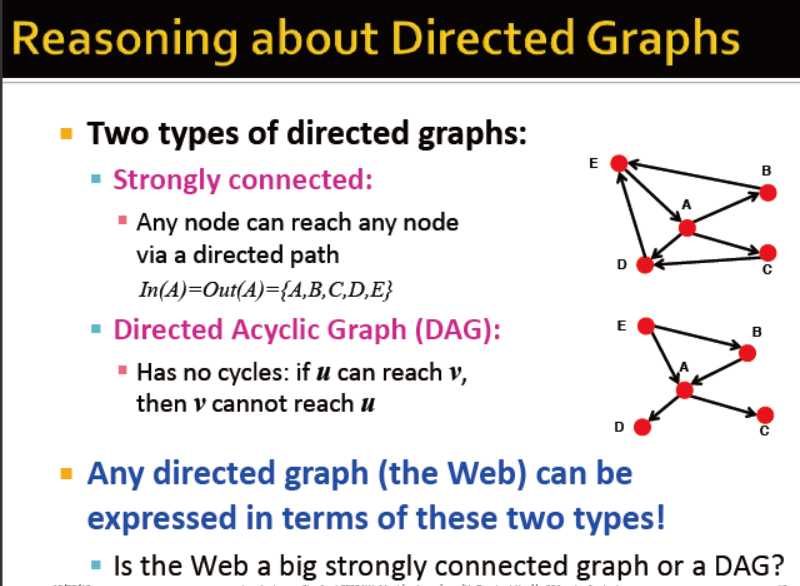
强连通分量：任意两节点有通路

事实上，每一个有向图在他的SCCs上都是有向无环图，也就是说，如果把一个图中的连通分量看成一个节点的话，那个这个虚拟的新图就是一个DAG

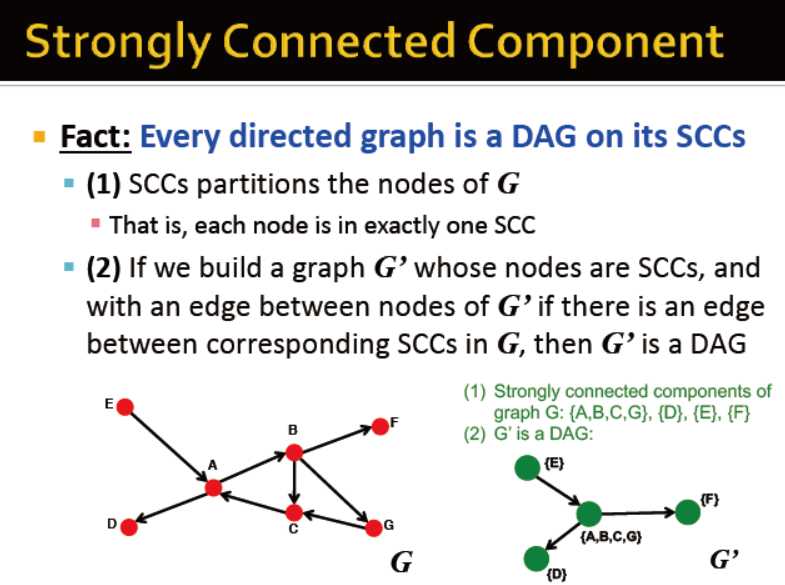
网络的结构：

一个节点的In(v)和Out(v)的交集，是一个强连通分量，同时=Out(v，G)与Out(v，G‘)交集，G‘是指G中所有边的方向翻转后得到的图

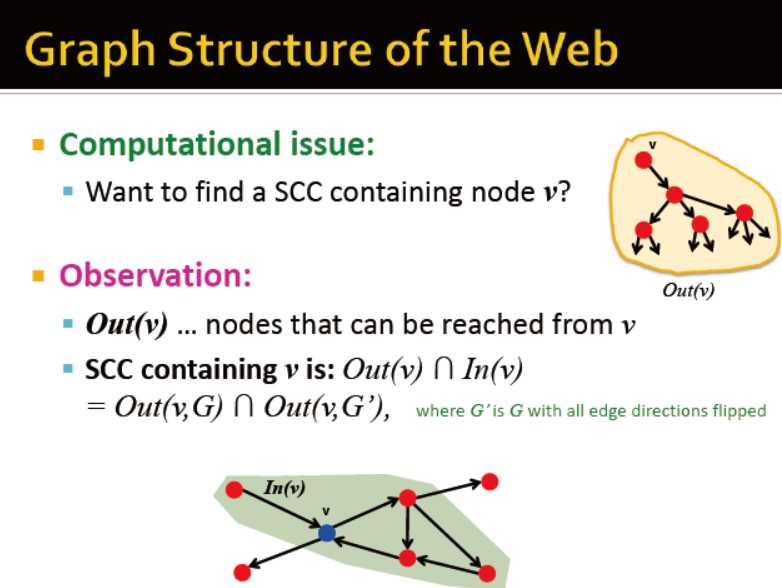
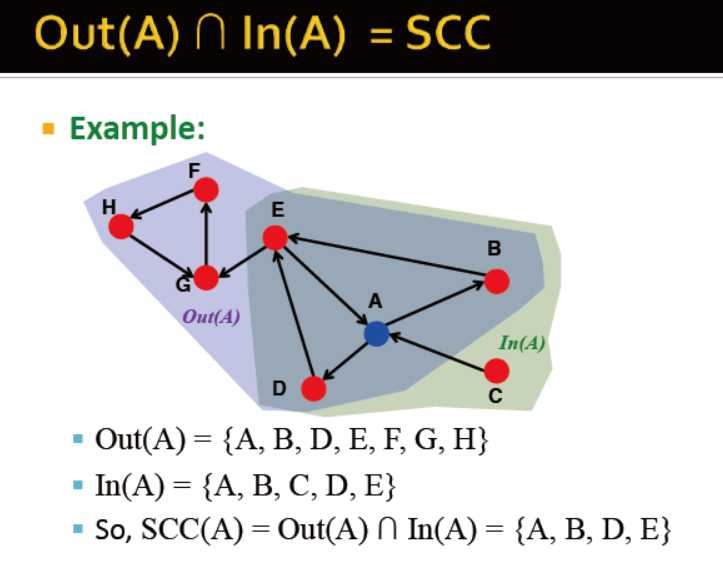
对于网页网络而言，计算其输入与输出分量

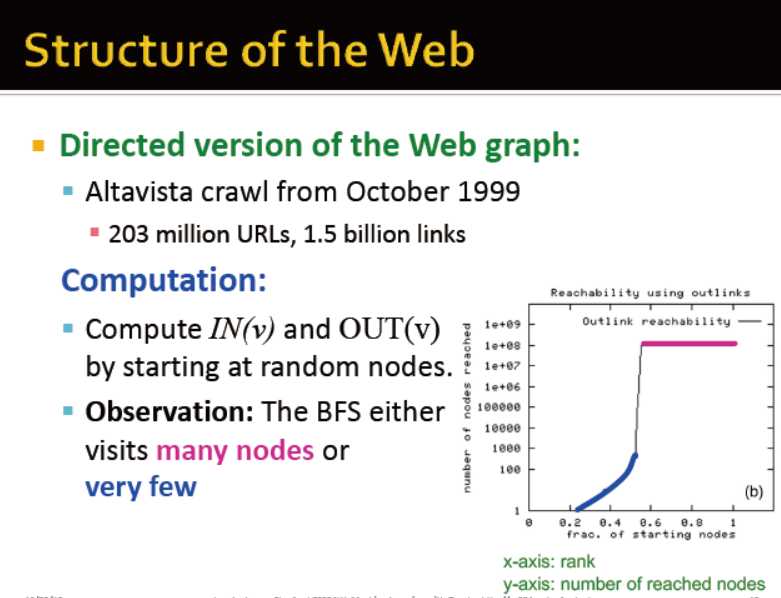
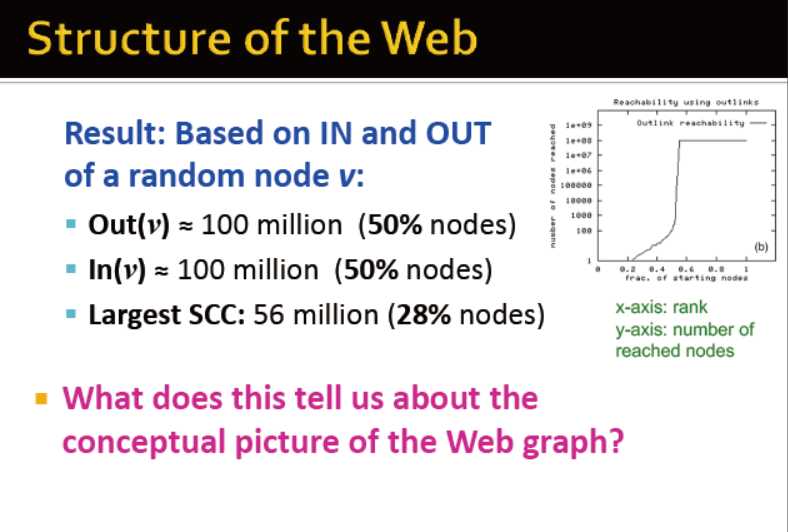
结果

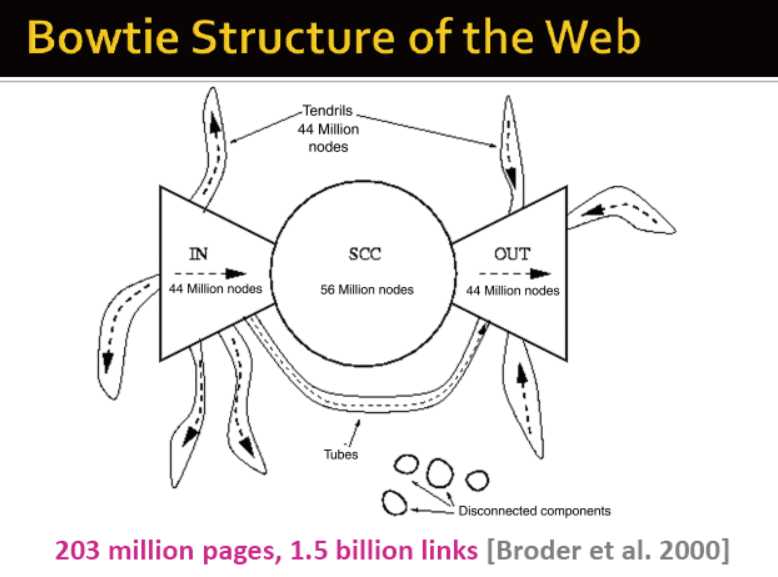
蝴蝶结结构

---

网络的pagerank

对网页的重要度进行排序——基于网络结构

链路分析算法

§ PageRank

§ Personalized PageRank

§ Random Walk with Restarts

将链接看成投票，网页越重要，则有更多的链接

但是，每一个链接都一视同仁吗？

从重要网页来的vote更具价值

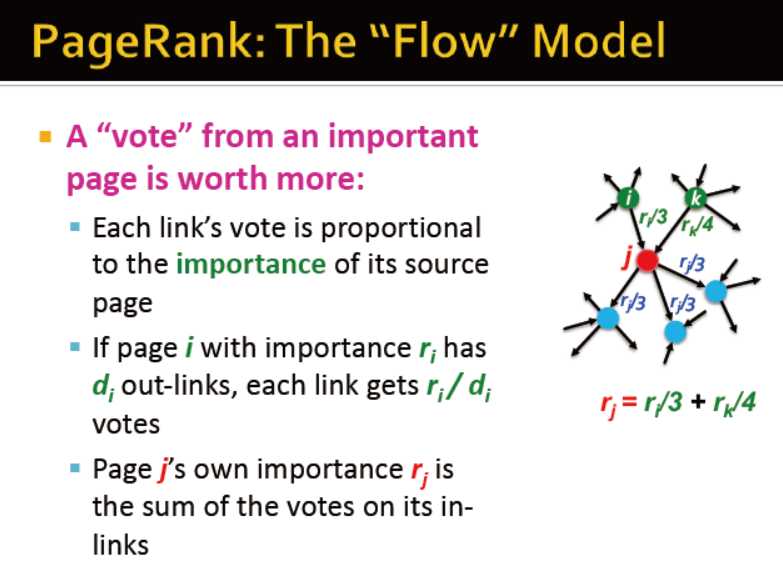
当一个节点被其他重要节点指向时，这个点变得更重要

矩阵公式

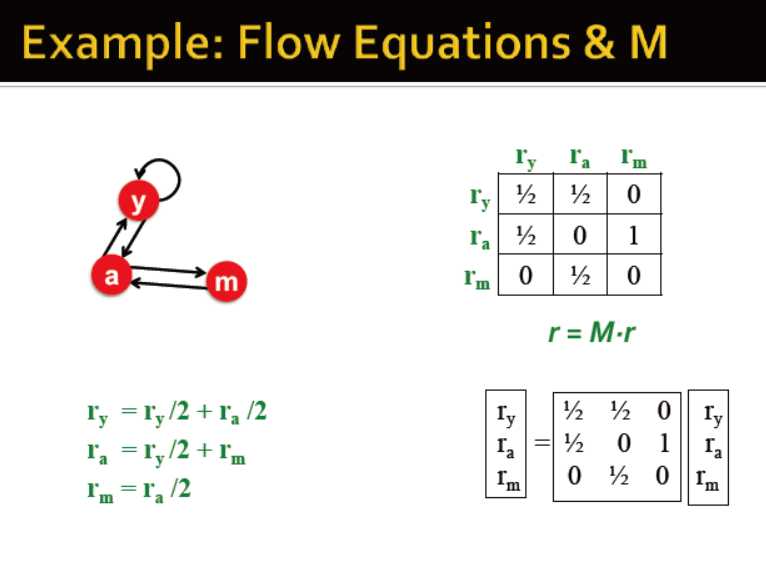
矩阵的特征向量M=pagerank

迭代方式

---

pageRank的解方程

3个问题：

是否收敛；收敛结果是所需求的吗？结果合理吗？

还有两个问题：

有些网页没有出度

有些网页是搜索陷阱，即所有的链接都在组内

对于上面的两个问题，那么，他会收敛吗？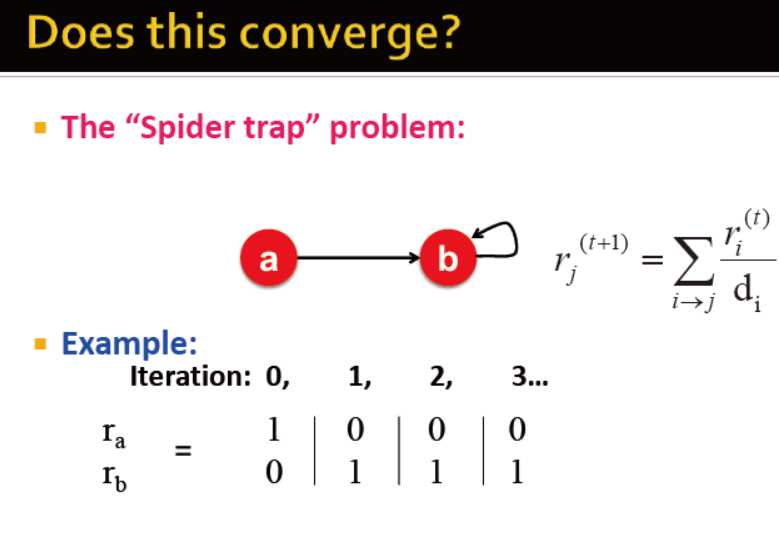

解决方案：

在每一次迭代，以某个概率随机链接？

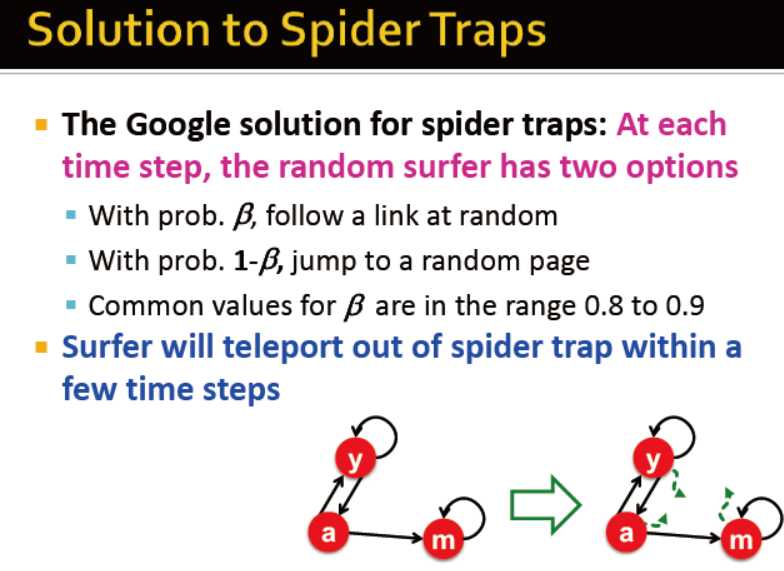
对于teleports，没有出度的，在矩阵中使其出度的概率为1

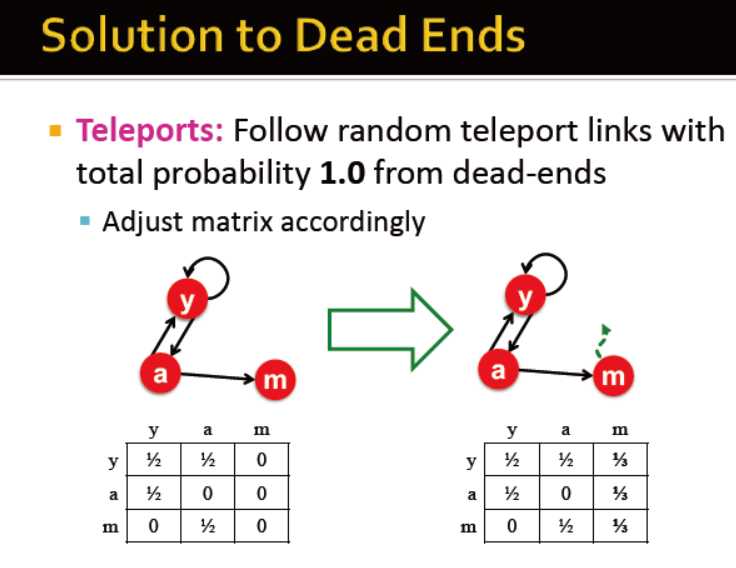
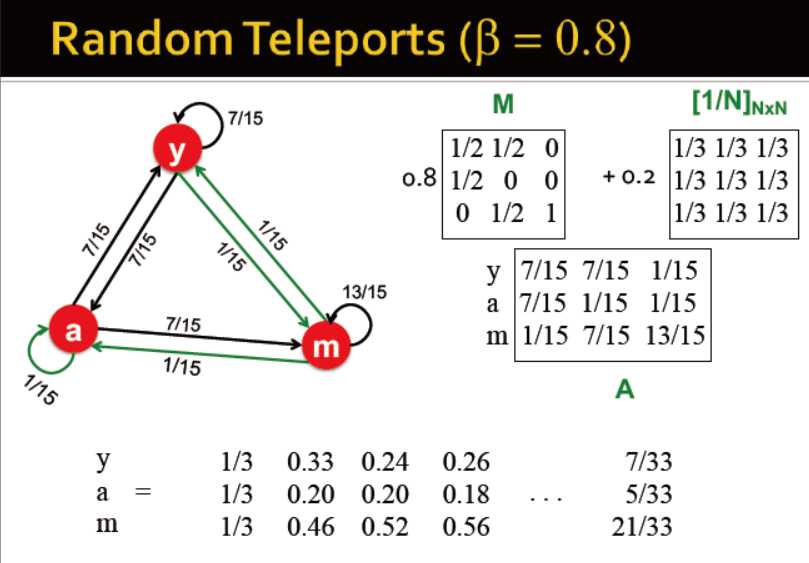
google的解决方案

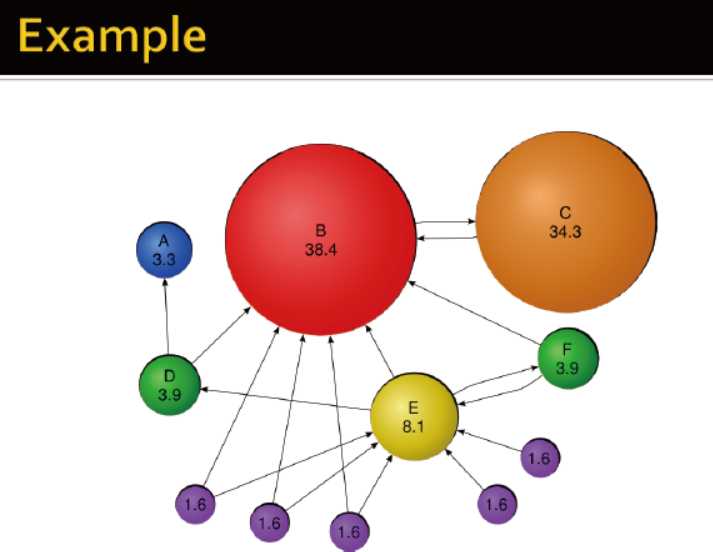
例子：

---

如何实际计算pagerank

当节点多的时候，占用空间大

通过稀疏矩阵的分解

例子：

随机游走的restart以及个性化的pagerank

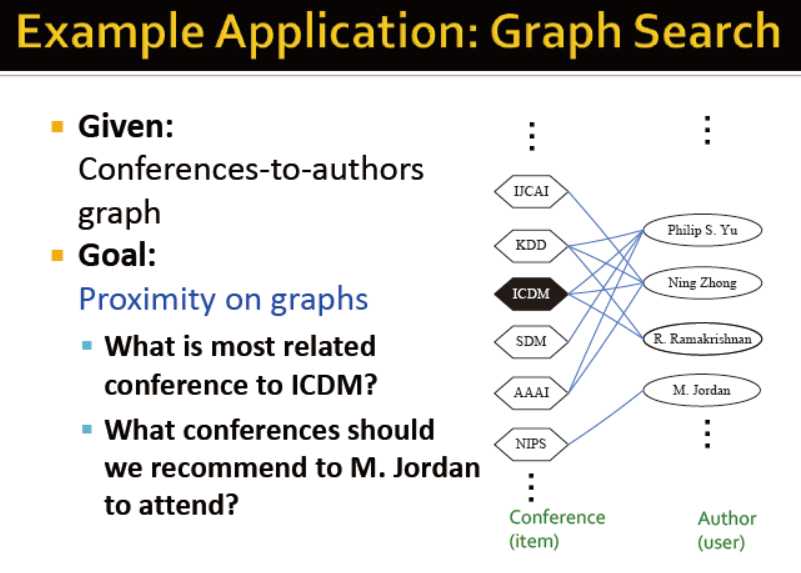
应用例子：图谱检索

给定：作者与会议的关联网络

目标：图谱中的相似衡量

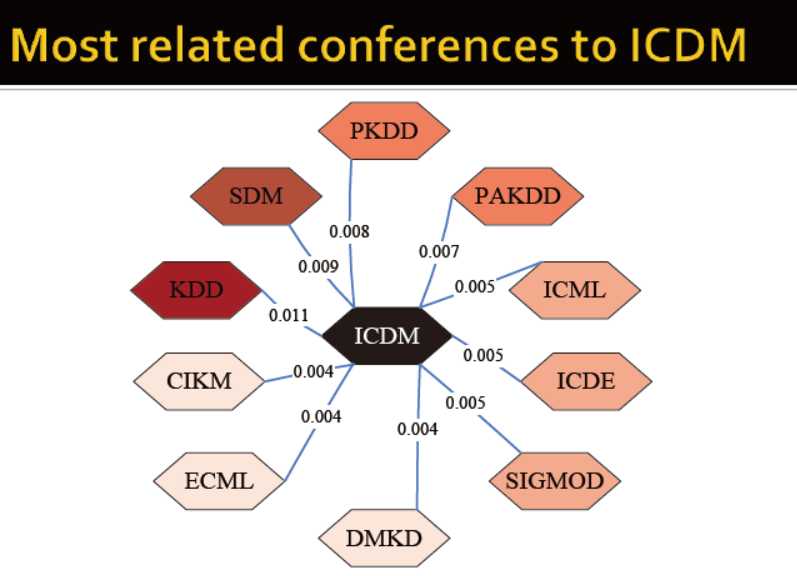
           如：与ICDM关联度最高的会议是？我们应该推荐某个人参加其他哪类会议？

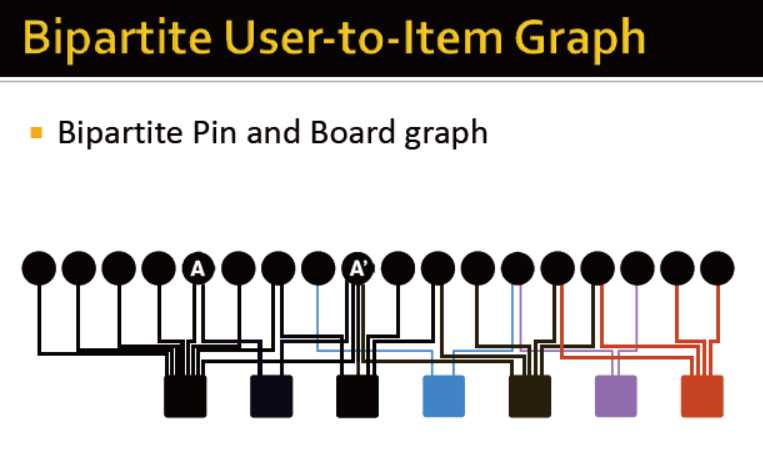
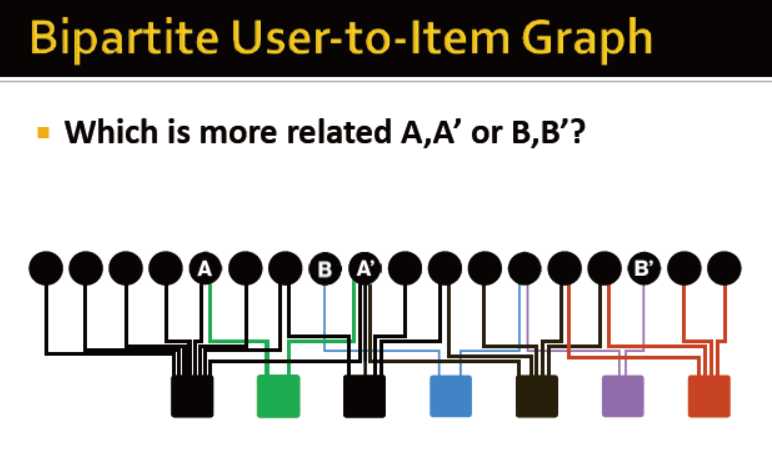
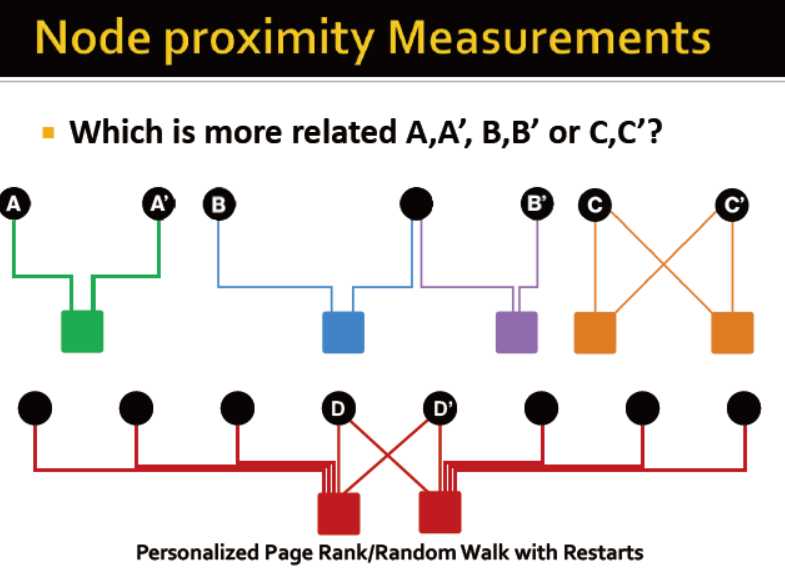
1） 图谱和网页检索：对节点基于重要性排序

2）个性化的PageRank：将节点与teleport node s的亲近度进行排序

3）图中的亲近度: 例如与ICDM最相关的是？重启动的随机游走，启动点位teleport node

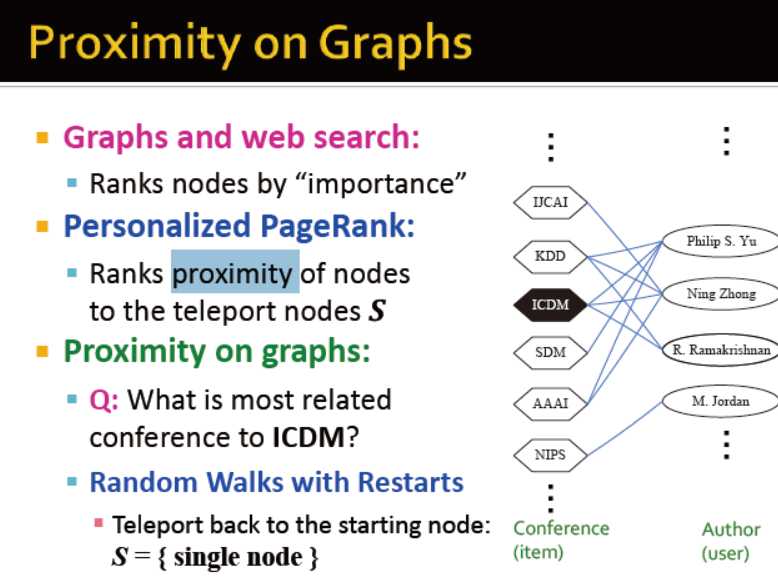
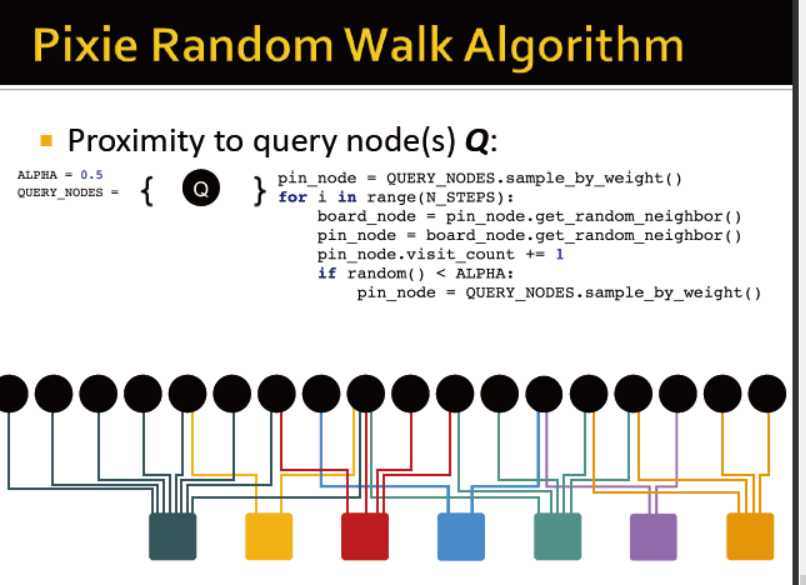
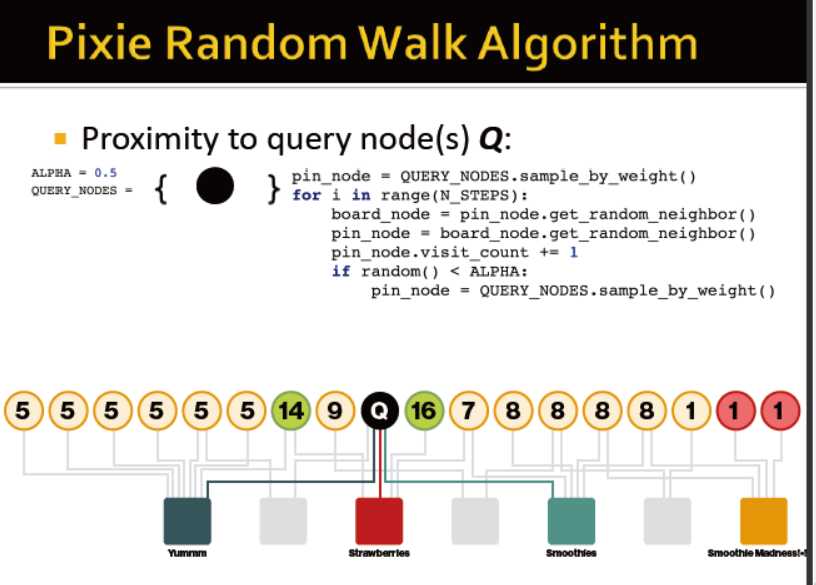
如何 random walk

1）从查询点出发，随机游走，并记录每个访问到的点

2）以概率α，多次随机游走

3）访问次数最多的点，即为最相近的点

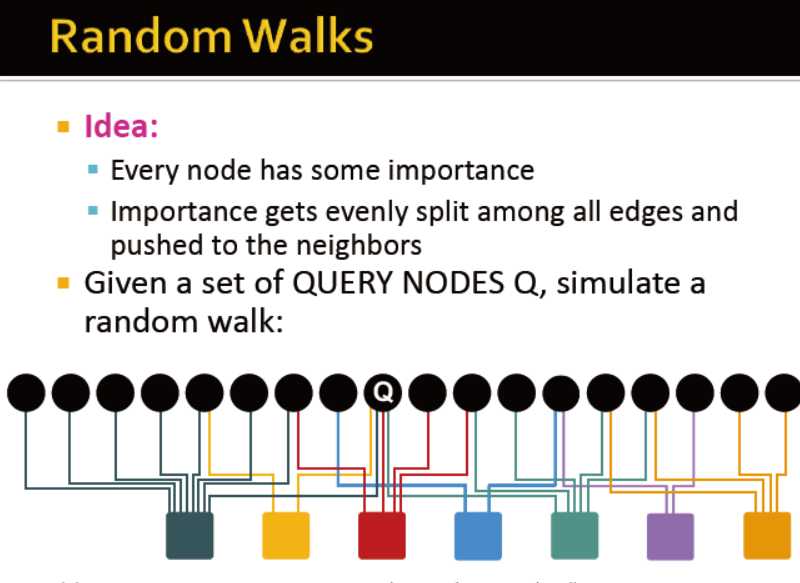
益处：

考虑了：多链接；多路径；有向和无向的连接；节点的度

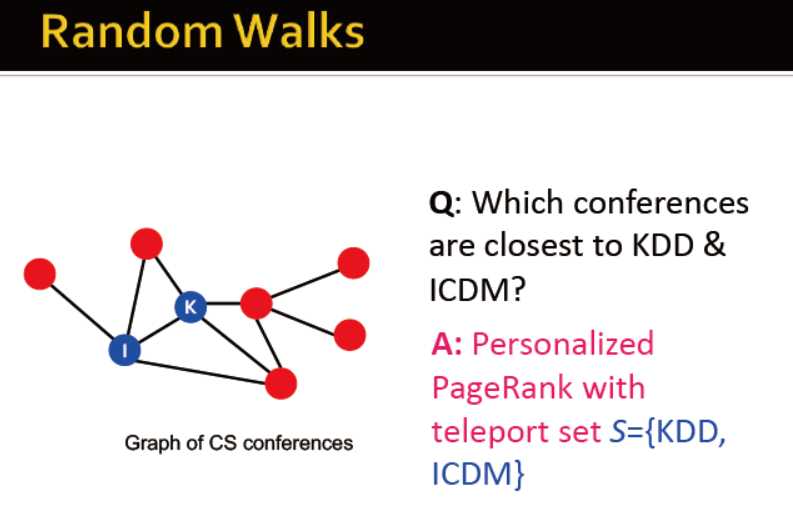
pagerank总结：

来自为知笔记(Wiz)