Educational Codeforces Round 80

Posted 2021-03-11 baihualiaoluan

QAQ：

其中C，D，E题的思路来自

https://www.bilibili.com/video/av83609526?p=5

A. Deadline

题意：

给出一个式子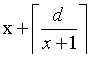对于给出的d，求当x是整数时的最小解。

思路：

简单数学题，这个式子变形一下就是我们中学学的对号函数，但要注意下向上取整和整数x

代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
int main()
{
    int T;
    LL n,d;
    cin >> T;
    while(T--)
    {
        cin >> n >>d;
        LL x = sqrt(d);
        if(d<=n)
        {
            printf("YES
");
            continue;
        }
        if(2*x-1>n)
            printf("NO
");
        else
        {
            if(x*x==d)
            {
                int ans = 2*x-1;
                if(ans<=n)
                    printf("YES
");
                else
                    printf("NO
");
            }
            else
            {
                int x1 = x,x2 = x+1;
                int ans1 = d/x1,ans2 = d/x2;
                if(d%x1)
                    ans1++;
                if(d%x2)
                    ans2++;
                ans1 += (x1-1);
                ans2 +=(x2-1);
                if(ans1<=n||ans2<=n)
                    printf("YES
");
                else
                    printf("NO
");
            }
        }
    }
    return 0;
}

B.  Yet Another Meme Problem

题意：

给你两个数，A,B，要求有多少对a,b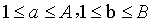（），满足a*b+a+b = conc(a,b)，其中conc(a,b),表示将a和b连接起来，例如conc(12,23) = 1223。

思路：

我们可以将给出的公式变一下形

 

 

 

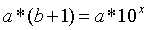
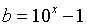
所以最终结果等于A*(满足上面取值的b的数目)。

代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
int main()
{
   int T;
   cin >> T;
   while(T--)
   {
       LL A,B;
       cin >> A >>B;
       B++;
       int cnt = 0;
       while(B)
       {
           cnt++;
           B/=10;
       }
       --cnt;
       cout << A*cnt << endl;
   }
    return 0;
}

C.  Two Arrays

题意：

给你两个数n,m，要求你用1-n中的数组成两个长为m的数组a,b，要求a数组非递减，b数组非递减，同时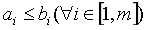，求这样的数组共有多少对（结果mod）

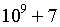思路：

根据上面的条件我们可以把上面两个数组倒接，如下所示

 

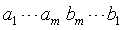
现在问题转化为用1-n中的数构造出一个长为2*m的非递减数组，问最多有多少组合。

我们可以用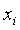表示i这个数选用了多少次。

那么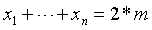

考虑组合数学来解决问题。

上面可转为2*m个球放进n个盒子，盒子可以为空的组合数，进而可以转为将2*m+n个球分成n份，每份不允许为空的方案数。

运用隔板法，那么最终答案是就是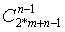

也就是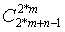，组合数取模的话，可以用卢卡斯定理 解决。

代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL mod = 1e9+7;
LL quick_pow(LL x, LL n, LL p)// 快速幂求x^n mod p 的结果
{
    if(n==0)
        return 1;
    if(n==1)
        return x%p;
    LL ans = 1;
    LL tmp = x%p;
    while(n)
    {
        if(n&1)
        {
            ans = (ans*tmp)%p;
        }
        tmp = tmp*tmp%p;
        n>>=1;
    }
    return ans%p;
}
LL inv(LL b,LL p) //求数 b mod p 的逆元
{
    return quick_pow(b,p-2,p);
}
LL C(LL n,LL m,LL p)//组合数取模
{
    if(m==0|| m== n)
        return 1;
    if(m==1||m==n-1)
        return n%p;
        m = min(m,n-m);
    LL up = 1,down = 1;
    for(LL i = n-m+1;i<=n;i++)
        up=(up*i)%p;
    for(LL i = 1;i<=m;i++)
        down*=i%p;
    up%=p;
    down%=p;
    return (up*(inv(down,p)%p))%p;
}
LL lucas(LL n,LL m,LL p)//递归lucas函数
{
    if(m==0)
        return 1;
    return lucas(n/p,m/p,p)*C(n%p,m%p,p)%p;
}
int main()
{
    LL n,m;
    cin >> n >> m;
    cout << lucas(2*m+n-1,2*m,mod);
    return 0;
}

D.  Minimax Problem

题意：

给你一个大小为n*m的矩阵，让你任取两行，取对应列的两个数的较大者构成新的一行，并使这一行中的最小的数最大。输出结果的两行（这两行可以是同一行）

思路：

最大化最小值的问题，考虑二分解决。但是二分的对象是那个最大的最小值。

这个题的check函数比较特殊。

观察题目，m的范围很小，我们可以将考虑将每一行映射成为二进制，具体规则是（假设check的数是k），这一行大于等于k的数为1，小于的为0，假如我们选出的两列或的结果就是合并出来的行二进制下的结果，如果结果大于（1<<m）-1，也就是二进制下m个1，就代表当前的这个数是可以的。具体细节可以代码。

代码：

#include <bits/stdc++.h>
using namespace std;
int n,m;
vector<vector<int> >a;
int a1,a2;
bool can(int mid)
{
    vector<int>msk(1<<m,-1);
    for(int i = 0;i<n;++i)
    {
        int cur =0;
        for(int j = 0;j<m;++j)
        {
            if(a[i][j]>=mid)
                cur^=(1<<j);
        }
        msk[cur] = i;
    }
    if(msk[(1<<m)-1]!=-1)
    {
        a1 = a2 =msk[(1<<m)-1];
        return true;
    }
    for(int i = 0;i<(1<<m);++i)
        for(int j = 0;j<(1<<m);++j)
    {
        if(msk[i]!=-1&&msk[j]!=-1&&(i|j)==(1<<m)-1)
        {
            a1 =msk[i];
            a2 =msk[j];
            return true;
        }
    }
    return false;
}
int main()
{
    scanf("%d %d",&n,&m);
    a.resize(n,vector<int>(m));
    for(int i= 0;i<n;++i)
        for(int j = 0;j<m;++j)
            scanf("%d",&a[i][j]);
    int lf =0;
    int rg = int(1e9)+43;
    while(rg-lf>1)
    {
        int m = (lf+rg)/2;
        if(can(m))
        lf = m;
        else
            rg = m;
    }
    printf("%d %d
",a1+1,a2+1);
    return 0;
}

E.  Messenger Simulator

题意：

给你一个1-n的序列，输出m个数（1-n之间），代表把这数提到首位，求每个数在序列里的最小最大位置。

思路：

可以考虑在1-n之前插入m个空位，构成一个长为n+m的数组，假设是第i次输入的数是x，就把x放在m-i+1的位置，这个数原先所在的位置变成0，每次更新下所求的两个值，最后再更新一下即可，整个结构可以用树状数组来维护，具体细节可以代码。

代码：

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6+7;
int n,m;
int a[maxn],d[maxn],mx[maxn],mn[maxn];
int pos[maxn];
int lowbit(int x)
{
    return x&(-x);
}
void update(int x,int y)
{
    for(int i =x;i<maxn;i+=lowbit(i))
        d[i]+=y;
}
int get(int x)
{
    int ans =0;
    for(int i =x;i;i-=lowbit(i))
        ans+=d[i];
    return ans;
}
int main()
{
    cin >> n >> m;
    for(int i =1;i<=n;++i)
    {
        mx[i] = mn[i] = i;
        pos[i] = i+m;
        update(i+m,1);
    }
    for(int i =0;i<m;++i)
    {
        int x;
        cin >> x;
        mx[x] = max(mx[x],get(pos[x]));
        mn[x] = 1;
        update(pos[x],-1);
        pos[x] = m-i;
        update(pos[x],1);
    }
    for(int i = 1;i<=n;++i)
    {
        mx[i] = max(mx[i],get(pos[i]));
    }
    for(int i = 1;i<=n;++i)
        cout << mn[i] << " " << mx[i] << "
";
    return 0;
}