ST表超级详解

Posted 2021-03-11 soul-maker

 ST表超级详解

       关于ST表，有很多文章，这里本蒟蒻也来发一波~~ 希望能为您提供帮助~~

     1.ST表的介绍

     ST表算法全称Sparse-Table算法，是由Tarjan提出的一种解决RMQ问题（区间最值）的强力算法。离线预处理时间复杂度 θ（nlogn），在线查询时间 θ（1），可以说是一种非常高效的算法。不过ST表的应用场合也是有限的，它只能处理静态区间最值，不能维护动态的，也就是说不支持在预处理后对值进行修改。一旦修改，整张表便要重新计算，时间复杂度极高。动态最值可以用线段树、树状数组等来维护。

     2.ST表的一般实现

     ST表之所以广为使用，不仅因为它的时间复杂度优秀，还因为它的代码思路比较清晰，码量比较合适。核心的代码主要集中预处理和查询上。那么接下来我们就先来讲讲它的预处理（下面都以区间最小值来讲，最大值可以类推）。设st[i][j]表示从第 i 个数起向后连续2^j个数中的最小值。注意，是包括第 i 个数在内的2^j个数。那么，我们可以得到转移方程：

     1.st[i][0]=第i个数（很明显，2^0==1，从第i个数起向后数1个数，当然只有它自己。)

     2.st[i][j]=min{ st[i][j-1] , st[i+(1<<j-1)][j-1]}（j≠0）(其实也挺好理解的。请看下图：）

                                                      

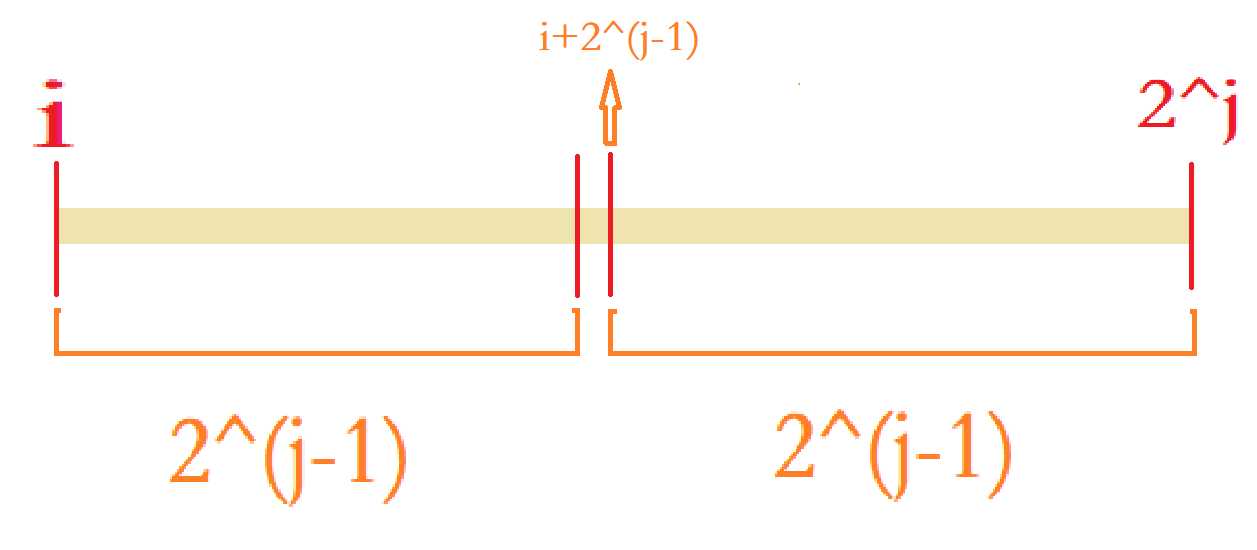
      （把整个2的j次方区间分成两个2^(j-1)区间，那么整个大区间的最小值就是两个已计算过的区间最小值的最小值。第一个区间很明白，是st[i][j-1]，就是从左端点 i 起向右数2^(j-1) 个数。第二个区间长度还是2^(j-1)，但是左端点需要由 i 加上上一个区间的长度，毕竟它们是连在一起的。1<<j-1 就是2^(j-1)。）

    以上，就是ST表的初始化部分。

    接下来，我们来讲讲查询。假设每次查询的左右端点分别为le和ri。思路：首先找到一个值k，k的含义是“最大的2^k不超过查询区间长度（ri-le+1）”。举个例子：le=1，ri=9，那么k最大为3，2^k==8,不超过区间长度。那么我们找两个长度为2^k的区间，一个以le为左端点，一个以ri为右端点。由于k最大，所以可以肯定，这两个小区间一定覆盖了整个大区间（一定的！！！不信可以自己试验）。那么，虽然两个小区间会有重叠部分，但是这里要求的是最小值，而非求和，所以这两个小区间最小值中的最小值，一定是整个区间的最小值！

    再细一点的说，一个区间为st[le][k],还有一个为st[ri-(1<<k)+1][k](这个能理解吧？1<<k就是2^k),那么：

    查询函数query(le,ri)=min{st[le][k],st[ri-(1<<k)+1][k]}。再次强调：重叠的小区间不影响整个区间的最小值！

    再总结一下查询的过程：1.找到k    2.返回两个st之间的最值  3.美妙结束。

    到这里，ST表的一般实现已被剖析完毕。有意思吧？

    3.ST表的重点思想拆解及注意事项

    ST表的确是一个不俗的数据结构。它背后运用到的算法思想也值得我们深究。主要有动态规划和倍增。在进行初始化的时候，运用了动归思想，逐步完善st数组。在整个算法中，倍增思想都一直贯彻其中，使整个算法的时间复杂度降了一个log级别，非常高效。在查询的时候，利用到了最小值不受区间重叠干扰的性质，所以可以巧妙地使用倍增。精髓！

    还有以下注意事项要提一提：1.在定义st数组的时候，第一维定义元素个数，那第二维的j怎么定义呢？还是很简单，j就像上文的k一样，定为“最大的2^j不超过最多元素个数”。如最多100000个数，那么j最大16，2^16==65536， 不超过100000。2.ST表的实践其实很广，很多时候会作为其他算法的辅助，应仔细思考。3.ST表代码中，对区间的边边角角操纵较多，需要以清醒的头脑对待，不要混了。

    4.上代码！！

    说了这么多，不看一下代码还是不行滴~~献上我丑陋的代码！

 

 1 #include<bits/stdc++.h>
 2 #define gc getchar() 
 3 #define MX 100005
 4 using namespace std;
 5 int m,ans[MX],st[MX][16];
 6 void q_in(int &x){
 7     x=0;int f=1;char c=gc;
 8     while(!isdigit(c)){if(c==‘-‘)f=-1;c=gc;}
 9     while(isdigit(c)){x=(x<<3)+(x<<1)+c-48;c=gc;}
10     x*=f;
11 }//读入优化
12 void getrd(){
13     for(int j=1;(1<<j)<=m;j++)
14         for(int i=1;i+(1<<j)-1<=m;i++)
15             st[i][j]=min(st[i][j-1],st[i+(1<<j-1)][j-1]);
16 }//预处理
17 int query(int le,int ri){
18     int k=0;while(le+(1<<k+1)-1<=ri)k++;
19     return min(st[le][k],st[ri-(1<<k)+1][k]);
20 }//查询
21 int main(){
22     int n;q_in(m);q_in(n);
23     for(int i=1;i<=m;i++)q_in(st[i][0]);
24     getrd();
25     for(int i=1;i<=n;i++){
26         int le,ri;q_in(le);q_in(ri);ans[i]=query(le,ri);
27     }
28     for(int i=1;i<=n;i++)cout<<ans[i]<<‘ ‘;//ans保留每次查询的答案
29     return 0;
30 } 

 

    谢谢大家！！！