GMOJ4015数列

Posted 2021-03-11 stoorz

题目

题目链接：https://gmoj.net/senior/#main/show/4015

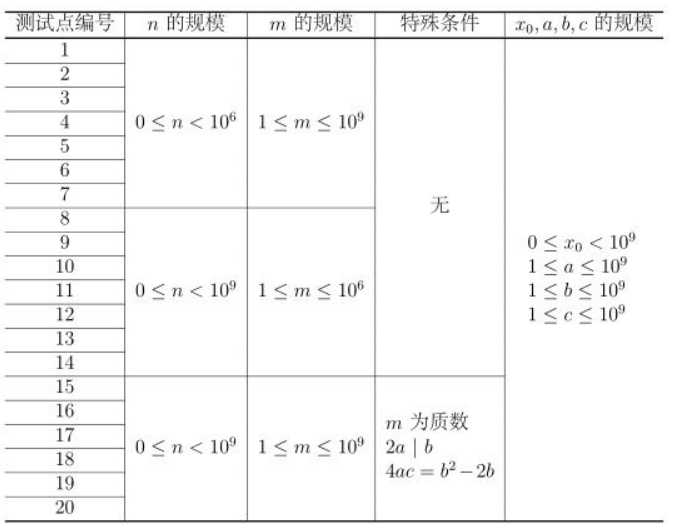
思路

分三个(sub)。分值分别为(35pts,35pts,30pts)。

sub1

(nleq 10^6),直接暴力递推即可。

sub2

(mleq 10^6)，显然(x_imod p)存在长度不超过(10^6)的循环节，直接找循环节即可。

sub3

特殊限制(min prime,2a|b,4ac=b^2-2b)，发现和二次函数很像。
不妨设二次函数(y=ax^2+bx+c)，其中(y)就是(x_i)，(x)就是(x_{i-1})。
(2a,b,4ac)等都与顶点式有关，所以将这个二次函数化为顶点式
[y=a(x+frac{b}{2a})^2+frac{4ac-b^2}{4a}]
[y=a(x+frac{b}{2a})^2-frac{b}{2a}]
[y+frac{b}{2a}=a(x+frac{b}{2a})^2]
那么明显有
[a(y+frac{b}{2a})=[a(x_0+frac{b}{2a})]^{2^n}]
即
[x_n=a^{2^n-1} imes (x_0+frac{b}{2a})^{2^n}-frac{b}{2a}]
因为(m)是质数，所以(a^pmod m=a^{pmod varphi(m)}mod m)。

代码

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;

const int N=1000010;
ll x,a,b,c,n,p,t[N],vis[N];

ll power(ll x,ll k,ll MOD)
{
    ll ans=1; x%=MOD;
    for (;k;k>>=1,x=x*x%MOD)
        if (k&1) ans=ans*x%MOD;
    return ans;
}

void solve1()
{
    for (int i=1;i<=n;i++)
        x=(a*x%p*x%p+b*x%p+c)%p;
    printf("%lld",x%p);
}

void solve2()
{
    int m=0;
    x%=p;
    for (;;m++)
    {
        if (vis[x]) 
        {
            n-=vis[x]; m-=vis[x];
            printf("%lld",t[n%m+vis[x]]);
            break;
        }
        vis[x]=m; t[m]=x;
        x=(a*x%p*x%p+b*x%p+c)%p;
    }
}

void solve3()
{
    ll k1=(power(2,n,p-1)-1+p-1)%(p-1);
    ll k2=power(2,n,p-1);
    printf("%lld",((power(a,k1,p)*power(x+b/2/a,k2,p)-b/2/a)%p+p)%p);
}

int main()
{
    scanf("%lld%lld%lld%lld%lld%lld",&x,&a,&b,&c,&n,&p);
    if (n<=1000000LL) solve1();
    else if (p<=1000000LL) solve2();
    else solve3();
}