20190704考试总结

Posted 2021-03-10 lcguo

1.质因数分解

【问题描述】

Pluto 最近的数学水平正在迅速下降，连他自己都觉得自己已经没救了。

现在，Pluto 发现自己连最基本的质因数分解都不会做了，他只能来求助你了。

【输入格式】

第一行一个正整数 t，表示数据的组数。

接下来 t 行，每行一个正整数 n，表示带分解的数。

【输出格式】

共 t 行。

每行若干个用空格隔开的正整数，从小到大排列，表示 n 的质因数分解结果。

【样例输入】

 2
 7
 12

【样例输出】

 7
 2 2 3

【数据规模和约定】

对于 30%的数据，2 ≤ n ≤ 1000000。

对于 60%的数据，2 ≤ n ≤ 1000000000。

对于 100%的数据，2 ≤ n ≤ 1000000000000，t ≤ 20。

刚开始看着一眼，哇(2 ≤ n ≤ 1000000000000)要死了

后来一想。。。质因数分解如果用试除法的话，时间复杂度就是(O(sqrt{n}))

然后初一数学知识可以求出(sqrt{1000000000000}=1000000)是不会超时的

于是就可以打模板，如下：

#include<bits/stdc++.h>
using namespace std;
long long t,num,p[1000100];
long long n;
int main(){
    scanf("%lld",&t);
    for(int i=1;i<=t;i++){
        scanf("%lld",&n);
        int num=0;
        for(int i=2;i<=sqrt(n)+1;i++)
            while(n%i==0){
                p[++num]=i; n=n/i;
            }
        if(n>1) p[++num]=n;
        sort(p+1,p+num+1);
        for(int i=1;i<=num;i++)
            printf("%lld ",p[i]); 
        printf("
");
    }
    return 0;
}

判断输出就好了，如果不sort就会导致输出的顺序不是由小到大，就会WA

另外，该题的(i<=sqrt(n))不可以写成(i*i<=n)不然会爆long long，然后会炸。。。

代码中还要开long long不然也会炸。。。

ps.试除法:扫描2~sqrt(n)之间的每一个数d，在n中除去所有的d同时累计数量

---

2.蛇形方阵2

【问题描述】

大家一定都听说过蛇形矩阵，也一定都听说过螺旋矩阵，但一定没有听过蛇形螺旋矩阵。所谓蛇形螺旋矩阵，是非常类似于螺旋矩阵的一种矩阵。

它们仅有的不同之处在于：螺旋矩阵总是按顺时针方向旋转并填入相应数字，而蛇形螺旋矩阵每一圈的旋转方向是不固定的。

现在给出一个蛇形螺旋矩阵的大小，同时给出每一圈旋转的方向，请你制作出这个矩阵。（特别说明：第 i 圈的旋转是从（i，i）处开始的。）

【输入格式】

第一行一个正整数 n，表示蛇形螺旋矩阵的边长。

第二行（n+1）/2 个整数，第 i 个数表示从外向内第 i 圈的旋转的方向。1 表示顺时针方向，-1 表示逆时针方向。

【输出格式】

输出共 n 行，每行 n 个用空格隔开的正整数，第 i 行第 j 个整数表示这个矩阵（i，j）处的应填的整数。

【样例输入】

 7
 1 -1 -1 1

【样例输出】

 1 2 3 4 5 6 7
 24 25 40 39 38 37 8
 23 26 41 48 47 36 9
 22 27 42 49 46 35 10
 21 28 43 44 45 34 11
 20 29 30 31 32 33 12
 19 18 17 16 15 14 13

【数据规模和约定】

对于 50%的数据，1 ≤ n ≤ 100。

对于 100%的数据，1 ≤ n ≤ 1000。

这就是一道模拟题，反正我是按模拟做的

模拟顺时针的情况

if((n+1)/2-x==0&&(n+1)%2==0){a[x][x]=++num; return;}//神奇的特判
for(int i=x;i<=n-x+1;i++) a[x][i]=++num;
for(int i=x+1;i<=n-x;i++) a[i][n-x+1]=++num;
for(int i=n-x+1;i>=x;i--) a[n-x+1][i]=++num;
for(int i=n-x;i>x;i--) a[i][x]=++num;

模拟拟逆时针的情况

if((n+1)/2-x==0&&(n+1)%2==0){a[x][x]=++num; return;}//神奇的特判
for(int i=x;i<=n-x+1;i++) a[i][x]=++num;
for(int i=x+1;i<=n-x;i++) a[n-x+1][i]=++num;
for(int i=n-x+1;i>=x;i--) a[i][n-x+1]=++num;
for(int i=n-x;i>x;i--) a[x][i]=++num;

然后。。。就没有然后了

#include<bits/stdc++.h>
using namespace std;
int a[1001][1001],num,n,fx;
void ssz(int x,int y){
    if((n+1)/2-x==0&&(n+1)%2==0){a[x][x]=++num; return;}
    for(int i=x;i<=n-x+1;i++) a[x][i]=++num;
    for(int i=x+1;i<=n-x;i++) a[i][n-x+1]=++num;
    for(int i=n-x+1;i>=x;i--) a[n-x+1][i]=++num;
    for(int i=n-x;i>x;i--) a[i][x]=++num;
}
void nsz(int x,int y){
    if((n+1)/2-x==0&&(n+1)%2==0){a[x][x]=++num; return;}
    for(int i=x;i<=n-x+1;i++) a[i][x]=++num;
    for(int i=x+1;i<=n-x;i++) a[n-x+1][i]=++num;
    for(int i=n-x+1;i>=x;i--) a[i][n-x+1]=++num;
    for(int i=n-x;i>x;i--) a[x][i]=++num;
}
int main(){
    scanf("%d",&n);
    for(int i=1;i<=(n+1)/2;i++){
        scanf("%d",&fx);
        if(fx==1) ssz(i,num);
        else nsz(i,num);
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++)
            printf("%d ",a[i][j]);
        printf("
");
    }
    return 0;
}

3.大采购

【问题描述】

Pluto 所在的学校终于放假了，Pluto 决定好好犒劳一下自己，所以当然要去大采购了。

由于 Pluto 力量有限，他只能搬运最多不超过 w 个单位重量的物品。

在超市中，Pluto 一共看到了 n 样想买的东西，并且第 i 件商品每件重量为 ai，每件能带给 Pluto 的愉悦程度为 ci，其存货量为 mi。

现在，Pluto 想在能够搬走所买商品的前提下，得到尽量大愉悦程度。你能帮帮他吗?

【输入格式】

第一行两个正整数 n，w，含义见题面。

接下来 n 行，每行三个整数，第 i+1 行的整数分别表示 ai，ci，mi。

【输出格式】

一行一个整数，表示 Pluto 最大的愉悦程度。

【样例输入】

 4 15
 5 6 4
 3 4 3
 1 1 5
 2 3 3

【样例输出】

 21

【数据规模和约定】

对于 50%的数据，n ≤ 200，w ≤ 3000 ，mi ≤ 100。

对于 100%的数据，n ≤ 500，w ≤ 10000 ，mi ≤ 1000，ai ≤ 100，ci ≤ 1000。

裸的多重背包啊！！！

不会多重背包的左转，我不做解释

代码如下：

#include<bits/stdc++.h>
using namespace std;
int n,c,f[11111],a[511],v[511],w[511];
int main(){
    scanf("%d%d",&n,&c);
    for(int i=1;i<=n;i++)
        scanf("%d%d%d",&w[i],&v[i],&a[i]);
    for(int i=1;i<=n;i++){
        if(w[i]*a[i]>c){
            for(int j=0;j<=c;j++)
                if(j>=w[i]) f[j]=max(f[j],f[j-w[i]]+v[i]);
        }
        else{
            int k=1,mo=a[i];
            while(k<mo){
                for(int j=c;j>=k*w[i];j--)
                    f[j]=max(f[j],f[j-k*w[i]]+k*v[i]);
                mo-=k; k+=k;
            }
            for(int j=c;j>=mo*w[i];j--)
                f[j]=max(f[j],f[j-mo*w[i]]+mo*v[i]);
        }
    }
    printf("%d",f[c]);
    return 0;
}

---

4.吉波那切数列

【问题描述】
有?个很著名的数列叫做斐波那契数列，它的定义式是

      Fn = Fn?1 + Fn?2

其中，递推的初始值为：F0 = 1, F1 = 1

在吉波那契数列这个问题中，我们相似地定义了?个吉波那契数列

      Gn = Gn?1 + Gn?2
      

对任何情况??，G0 = 1, ? G1 是?个随机的正整数 t。

现在告诉你 Gi 的值和两个正整数 i, j，请你求出 Gj。鉴于 Gj 可能很?，请你输出 Gj mod 19960515。

【输入格式】

有多组测试数据。第??是?个正整数 T，表示测试数据的组数。

接下来 T ?，每?为?组测试数据，每组测试数据包含 3 个正整数 i, Gi, j。

【输出格式】

于每组数据，输出 Gj mod 19960515。

如没有合适的 t，请输出 ?1。

【样例输入】

 2
 1 1 2
 3 5 4

【样例输出】

 2
 8

【数据规模与约定】

对于 30% 的数据，每个 Gibonacci 数列的 G1 = t ≤ 50

对于 50% 的数据，有 T ≤ 30

对于 100% 的数据，有 T ≤ 10000, 1 ≤ i, j ≤ 100000, 0 ≤ Gi < 19960515

我们不妨写出 Gn 的前?项：

(G0 = 1)

(G1 = t)

(G2 = t + 1)

(G3 = 2t + 1)

(G4 = 3t + 2)

(G5 = 5t + 3)

将系数该为斐波那契数列，整理?下就是

(Gn = Fn1*1 + Fn2)

解方程回去就好了。

#include<bits/stdc++.h>
using namespace std;
int mod=19960515;
long long x,a,g,c,t,f[111111]={0,1};
int main(){
    scanf("%lld",&t);
    for(int i=2;i<=100000;i++)
        f[i]=(f[i-1]+f[i-2])%mod;
    for(int i=1;i<=t;i++){
        scanf("%lld%lld%lld",&a,&g,&c);
        x=(g-f[a-1])/f[a];
        if(x*f[a]!=g-f[a-1]||x<=0) printf("-1
");
        else printf("%lld
",(f[c]*x+f[c-1])%mod);
    }
    return 0;
}

---

5.魔塔

【问题描述】

魔塔是个经典的 RPG 游戏，不知道?家有没有玩过，?少在弱弱的出题?的童年，这是计算机对我??最重要的功能了……（出题?过于荒废?家千万不要学）这个游戏需要动很多脑筋，任何?个轻率的选择都可能导致游戏的失败。

魔塔游戏虽不?，但是制作精美，道具很多，?且难度不低，对智商是?次艰巨的考验。

现在让我们看?个简单的魔塔游戏：这个魔塔游戏中没有门，也没有特殊的道具，只有?种怪物和?些体??。

从出?点进?地图，你已经有 H 点初始体能，每打?个怪需要损耗 1 点体能，?吃到?个体能?可以得到 5 点体能。

勇?每次只能向上下左右四个?向?，如果要打怪或者喝体??，必须?到这点上。

如果体?为 0，我们的勇?仍然可以?动，但不能打怪了。

显然魔塔是有很多层的，因此我们希望能够尽量节省体?。为了能够更好地通关，也为了少杀?省?品，我们希望达到这层的终点时只要打最少的怪。

现在给你?张地图，请问最少打多少的怪才能?到终点。

【输入格式】

有多组数据，以 EOF 结束。对于每组数据：
第??：三个整数 H, N, M，表示初始体? H，以及地图有 N ? M 列。

第??开始的 N ?，描述了?个地图，其中 # 表示墙，M 表示怪物，C 表示体??，S 表示出?点，E 表示地图终点，“.”表示空位。详细请看样例。

【输出格式】

对每组数据输出??整数，表示最少需要打的怪的数量。

如果?法通关，请输出“Poor Warrior”（不含引号）

【样例输入】

 5 5 6
 S...MC
 .....M
 ......
 M#####
 MMMMME

【样例输出】

 7

【数据规模与约定】

总共有 3 个测试点

第?个测试点，没有体??，1 ≤ N, M ≤
6, H ≤ 10，共 3 组，30 分

第?个测试点，没有体??，1 ≤ N, M ≤ 10, H ≤ 10，共 2 组，30 分

第三个测试点，1 ≤ N, M ≤ 6，体??数量不超过 2 个，H ≤ 10，共 6 组，
40 分

最恶心的题出来了。

首先，明显这是一道搜索题，我们可以定义（x,y,h,k）来表示坐标，血量和杀敌数

然而，这会有反例

 4 5 4
 MMME
 M###
 MMMM
 S##C
 MMMM
 4 5 4
 MMMM
 S##C
 MMMM
 M###
 MMME

两个相反的图，如果正常来看，两组的答案应该是一样的，可是

或者或者

总之没有正确答案

这是为什么呢？

因为我们在搜索的过程中总会有一个顺序，

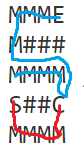
红色的是你的搜索顺序，但蓝色的线是正确的顺序，你就会发现，在蓝色的线搜到C时，你的红线早已经搜到过C，而当蓝线搜到C时，你剩余的血量，杀敌数，和坐标与先前红线相同
所以它会被当做重复搜索return掉

某蒟蒻lcg：那先向上搜不就好了吗；

然鹅。这就是这组数据的恶心的地方

如果你先向上搜的话，你第二组数据就错了！！！

。。。。。所以这是一个尴尬的时刻

突然，一只hzk大佬想出来了一个神奇的算法：随机数

。。。就是随机数

我们只要在搜索的过程中改变搜索的顺序

但由于这样搜索的正确率特别低，所以我们需要多搜几次取最小值

代码如下：

#include<bits/stdc++.h>
using namespace std;
int h,n,m,x,y,v[11][11][21][21],ans=INT_MAX;
int dx[5]={0,0,0,1,-1},dy[5]={0,1,-1,0,0};
char c[11][11];
void dfs(int x,int y,int nh,int ng){//搜索
    if(v[x][y][nh][ng]==1) return;//判断该状态是否出现过
    v[x][y][nh][ng]=1;
    int nb[5]={0,1,2,3,4};
    random_shuffle(nb+1,nb+5);//打乱顺序
    for(int i=1;i<=4;i++){
        int nx=x+dx[nb[i]],ny=y+dy[nb[i]];//随机移动
        if(nx>n||nx<=0||ny>m||ny<=0) continue;
        if(c[nx][ny]=='.') dfs(nx,ny,nh,ng);
        else if(c[nx][ny]=='E'){ans=min(ans,ng); return;}
        else if(c[nx][ny]=='M'&&nh>0){
            c[nx][ny]='.',dfs(nx,ny,nh-1,ng+1),c[nx][ny]='M';
        }
        else if(c[nx][ny]=='C') c[nx][ny]='.',dfs(nx,ny,nh+5,ng),c[nx][ny]='C';
    }
}
int main(){
    while(cin>>h>>n>>m){
        ans=INT_MAX;
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++){
                cin>>c[i][j];
                if(c[i][j]=='S') x=i,y=j;
            }
        for(int i=1;i<=100;i++) memset(v,0,sizeof(v)),dfs(x,y,h,0);//搜索一百遍，取最小值
        if(ans==INT_MAX) printf("Poor Warrior
");
        else printf("%d
",ans);
    }
    return 0;
}

简直是毒瘤

---

6.对战

【问题描述】

在?条街道上有 n 个?，他们都喜欢打乒乓球。

任意两个?的家的位置都不相同，按顺序标为 1, 2, · · · , n。

每个?都有?定的?平，用两两不等的整数表示。

当两个?想打球的时候，会找另?个?作为裁判，并到裁判家里进??场较量。出于某种原因，他们希望裁判的?平介于两?之间；同时，他们希望两个?到裁判家的总路程不超过两个?的家的距离。

对于两场较量，如果打球的两个?不完全相同或者裁判不同，我们就认为这两场较量不同。求不同的较量的总数。

【输入格式】

输?包含多组数据

输?的第??是?个整数 T，表示数据组数；

每组数据占??，包含 n + 1 个整数：n, a1, a2, · · · , an。其中 a1, a2, · · · , an
表示家位于相应位置的?的?平。

【输出格式】

对每组数据，用??输出?个整数，表示不同的较量的总数。

【样例输入】

 1
 3 1 2 3

【样例输出】

 1

【数据规模与约定】

对于 40% 的数据，有 n ≤ 1000；

对于所有数据，有 T ≤ 20, 3 ≤ n ≤ 100000，每个?的?平都是不超过
200000 的正整数。

这题显然是树状数组。。。

不会树状数组的左转。。。

我们先来语文分析一遍

他们希望裁判的?平介于两?之间

即a[i]<a[j]<a[k]（因为不会有相等的情况，所以不用考虑是否可以等于）

他们希望两个?到裁判家的总路程不超过两个?的家的距离

这句话就是说裁判要在他们两个人之间，这是很好理解的,如图：

当裁判在i的左边时，他们到裁判的距离绝对大于他们两人之间的距离，同理可证：当裁判在j的右边时，他们到裁判的距离也大于他们两人之间的距离；所以裁判只能在两个人之间

于是我们可以按顺序枚举中间点 i，那么问题就转换为了：求[1，i~1] 中比 a[i] 小/?的数有多少个、求 [i + 1; n] 中比 a[i]
小/?的数有多少个。求完之后运用乘法原理即可计算答案。

用树状数组，正着做?遍、反着做?遍。就ok了

#include<bits/stdc++.h>
using namespace std;
long long n,t,a[100001],c[205001],la[100001],li[100001],ra[100001],ri[100001];
long long ans,maxx=-1;
int lowbit(int x){
    return x&(-x);
}
void add(int x,int y){
    while(x<=maxx){
        c[x]+=y; x+=lowbit(x);
    }
}
int getsum(int k){
    int sum=0;
    while(k>0){
        sum+=c[k]; k-=lowbit(k);
    }
    return sum;
}
signed main(){
    scanf("%d",&t);
    for(int j=1;j<=t;j++){
        maxx=-1;
        memset(c,0,sizeof(c)); 
        ans=0;
        scanf("%d",&n);
        for(int i=1;i<=n;i++) scanf("%d",&a[i]),maxx=max(maxx,a[i]);
        for(int i=1;i<=n;i++){
            li[i]=getsum(a[i]-1);
            la[i]=i-li[i]-1; 
            add(a[i],1);
        }
        memset(c,0,sizeof(c));
        for(int i=n;i>=1;i--){
            ri[i]=getsum(a[i]-1);
            ra[i]=n-ri[i]-i;
            add(a[i],1);
        }
        for(int i=2;i<n;i++)
            ans+=(1LL)*li[i]*ra[i]+(1LL)*la[i]*ri[i];
        printf("%lld
",ans);
    }
    return 0;
}

---

题目比较良心，细细考虑应该没有问题的。。。吧