智能算法：蚁群算法

Posted 2021-03-10 kmxojer

作为一种现代智能算法，蚁群算法不需要任何先验知识，最初只是随机地选择搜索路径，随着对解空间的了解，搜索更加具有规律性，并逐渐得到全局最优解。目前，蚁群算法已被成功地应用于求解旅行商问题、车辆调度问题以及指派问题等。。。

求解TSP：

%% 第22章 蚁群算法的优化计算——旅行商问题(TSP)优化

%% 清空环境变量
clear all
clc

%% 导入数据
load citys_data.mat

%% 计算城市间相互距离
n = size(citys,1);
D = zeros(n,n);
for i = 1:n
    for j = 1:n
        if i ~= j
            D(i,j) = sqrt(sum((citys(i,:) - citys(j,:)).^2));
        else
            D(i,j) = 1e-4;      
        end
    end    
end

%% 初始化参数
m = 50;                              % 蚂蚁数量
alpha = 1;                           % 信息素重要程度因子
beta = 5;                            % 启发函数重要程度因子
rho = 0.1;                           % 信息素挥发因子
Q = 1;                               % 常系数
Eta = 1./D;                          % 启发函数
Tau = ones(n,n);                     % 信息素矩阵
Table = zeros(m,n);                  % 路径记录表
iter = 1;                            % 迭代次数初值
iter_max = 200;                      % 最大迭代次数 
Route_best = zeros(iter_max,n);      % 各代最佳路径       
Length_best = zeros(iter_max,1);     % 各代最佳路径的长度  
Length_ave = zeros(iter_max,1);      % 各代路径的平均长度  

%% 迭代寻找最佳路径
while iter <= iter_max
    % 随机产生各个蚂蚁的起点城市
      start = zeros(m,1);
      for i = 1:m
          temp = randperm(n);
          start(i) = temp(1);
      end
      Table(:,1) = start; 
      % 构建解空间
      citys_index = 1:n;
      % 逐个蚂蚁路径选择
      for i = 1:m
          % 逐个城市路径选择
         for j = 2:n
             tabu = Table(i,1:(j - 1));           % 已访问的城市集合(禁忌表)
             allow_index = ~ismember(citys_index,tabu);
             allow = citys_index(allow_index);  % 待访问的城市集合
             P = allow;
             % 计算城市间转移概率
             for k = 1:length(allow)
                 P(k) = Tau(tabu(end),allow(k))^alpha * Eta(tabu(end),allow(k))^beta;
             end
             P = P/sum(P);
             % 轮盘赌法选择下一个访问城市
             Pc = cumsum(P);     
            target_index = find(Pc >= rand); 
            target = allow(target_index(1));
            Table(i,j) = target;
         end
      end
      % 计算各个蚂蚁的路径距离
      Length = zeros(m,1);
      for i = 1:m
          Route = Table(i,:);
          for j = 1:(n - 1)
              Length(i) = Length(i) + D(Route(j),Route(j + 1));
          end
          Length(i) = Length(i) + D(Route(n),Route(1));
      end
      % 计算最短路径距离及平均距离
      if iter == 1
          [min_Length,min_index] = min(Length);
          Length_best(iter) = min_Length;  
          Length_ave(iter) = mean(Length);
          Route_best(iter,:) = Table(min_index,:);
      else
          [min_Length,min_index] = min(Length);
          Length_best(iter) = min(Length_best(iter - 1),min_Length);
          Length_ave(iter) = mean(Length);
          if Length_best(iter) == min_Length
              Route_best(iter,:) = Table(min_index,:);
          else
              Route_best(iter,:) = Route_best((iter-1),:);
          end
      end
      % 更新信息素
      Delta_Tau = zeros(n,n);
      % 逐个蚂蚁计算
      for i = 1:m
          % 逐个城市计算
          for j = 1:(n - 1)
              Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i);
          end
          Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i);
      end
      Tau = (1-rho) * Tau + Delta_Tau;
    % 迭代次数加1，清空路径记录表
    iter = iter + 1;
    Table = zeros(m,n);
end

%% 结果显示
[Shortest_Length,index] = min(Length_best);
Shortest_Route = Route_best(index,:);
disp([‘最短距离:‘ num2str(Shortest_Length)]);
disp([‘最短路径:‘ num2str([Shortest_Route Shortest_Route(1)])]);

%% 绘图
figure(1)
plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...
     [citys(Shortest_Route,2);citys(Shortest_Route(1),2)],‘o-‘);
grid on
for i = 1:size(citys,1)
    text(citys(i,1),citys(i,2),[‘   ‘ num2str(i)]);
end
text(citys(Shortest_Route(1),1),citys(Shortest_Route(1),2),‘       起点‘);
text(citys(Shortest_Route(end),1),citys(Shortest_Route(end),2),‘       终点‘);
xlabel(‘城市位置横坐标‘)
ylabel(‘城市位置纵坐标‘)
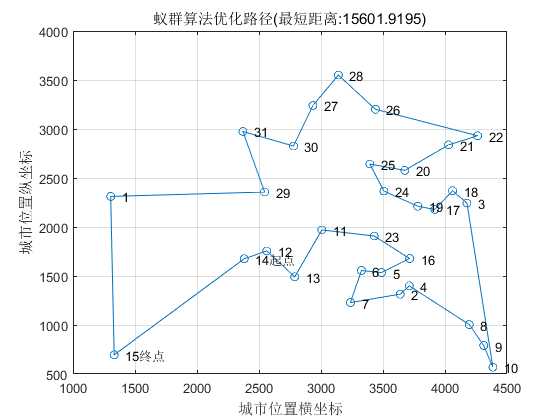
title([‘蚁群算法优化路径(最短距离:‘ num2str(Shortest_Length) ‘)‘])
figure(2)
plot(1:iter_max,Length_best,‘b‘,1:iter_max,Length_ave,‘r:‘)
legend(‘最短距离‘,‘平均距离‘)
xlabel(‘迭代次数‘)
ylabel(‘距离‘)
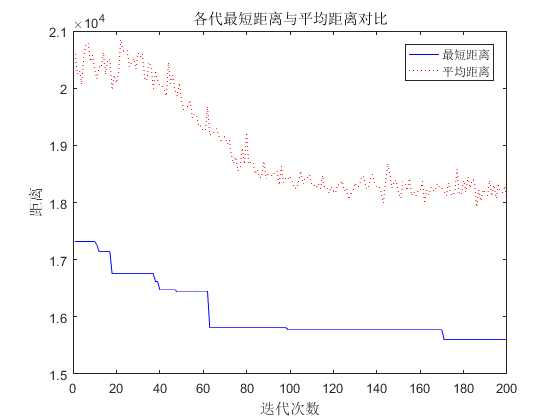
title(‘各代最短距离与平均距离对比‘)

蚁群算法优化路径：

 

 各代最短距离与平均距离对比：