数学建模系列：模糊综合评判法

Posted 2021-03-10 ch42e

原理

• 模糊集

  对于传统集合，一个元素要么属于这个集合，要么不属于这个集合，我们用1表示元素属于该集合，0表示元素不属于该集合。

  模糊集合论认为一个集合可以不完全属于一个集合，用[0，1]之间的一个数来表示一个元素属于一个集合的程度，这个数叫做该集合的隶属度

• 模糊概念的清晰化

  我们可以设定一个数（比如0.5）当一个元素的隶属度大于这个数时，我们就可以认为该元素时属于这个集合的

一级模糊综合评价

以人事考核为例，运用模糊综合评价，对企业员工的综合素质进行考核，从而为企业员工的升迁、评先晋级、聘用等提供依据。

具体步骤：

1. 确定因素集

   对于员工的表现，需要从多个方面进行综合评判，如员工的业绩、工作态度、沟通能力、政治表现等。所有的这些因素构成了评价指标体系集合，即因素集，记为：
   [ U={u_1,u_2,···,u_n } ]

2. 确定评语集

   由于每个指标的评价值不同，往往会形成不同的等级。由各种不同决断构成的集合称为评语集，记为：
   [ V={v_1,v_2,···v_n} ]

3. 确定各因素的权重

   而通常不同的因素在综合评价中所起到的作用也是不同的，综合评价的结果很大程度上还依赖于各因素对综合评价所起的作用，就需要确定一个各因素之间的权重分配，它是U上的一个模糊向量，记为：
   [ A=[a_1,a_2,···,a_n] ]
   上式中，(a_i)为第(i)个因素的权重，且满足(sum_{i=1}^na_i =1)

   确定权重的方法有：Delphi法、加权平均法、众人评估法等

4. 确定模糊综合判断矩阵

   对指标(u_i)来说，各个评语的隶属度为V上的模糊子集，对(u_i)的评判记为：
   [ R_i = [r_{i1},r_{i2},···,r_{im}] ]
   各指标的模糊判断矩阵为

   

   它是一个从U到V的模糊关系矩阵

5. 综合评判

   如果有一个从U到V的模糊关系(R=(r_{ij})_{m imes n})，那么利用R就可以得到一个模糊变换
   [ T_R：F(U) o F(v) ]
   由此变换就可以得到模糊评价结果B = A · R

   综合后的评判可以看作是V上的模糊向量，记为：
   [ B=[b_1,b_2,···,b_m] ]

   例子

   某单位对员工的年终综合评定：

   1. 因素集：U = {政治表现能力，工作能力，工作态度，工作业绩}

   2. 评语集：V = {优秀，良好，一般，较差，差}

   3. 确定各因素的权重：A = [0.25，0.2，0.25，0.3]

   4. 确定模糊综合评判矩阵，最每个因素作出评价，通过群众评议打分确定：
      [ R_1=[0.1,0.5,0.4,0,0] ]
      说明：参与打分的群众中，由10%的人认为政治表现优秀，50%的人认为政治表现良好....同样的方法评判其他因素

      得到评价矩阵：

      

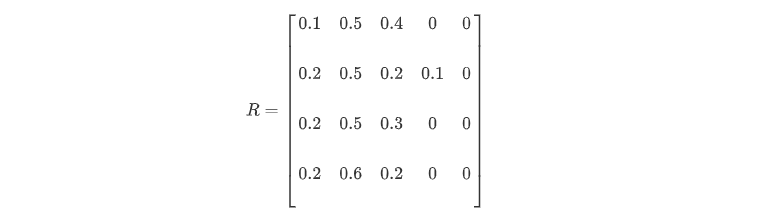
   5. 模糊综合评价，进行矩阵合成运算：

      

      得到：
      [ B =[0.175,0.53,0.275.0.02,0] ]
      取数值最大的评语作为综合评判结果为“良好”

多层次模糊综合评判

对于一些稍复杂的系统，需要考虑的因素很多，这时候仍旧使用一级模糊综合评判，可能会出现：（1）因素过多造成权数分配难以确定；（2）即便确定了权数分配，由于需要满足归一化条件，每个因素的权数都很小；对此可以采用多层次模糊综合评判方法。

如下面的例子：

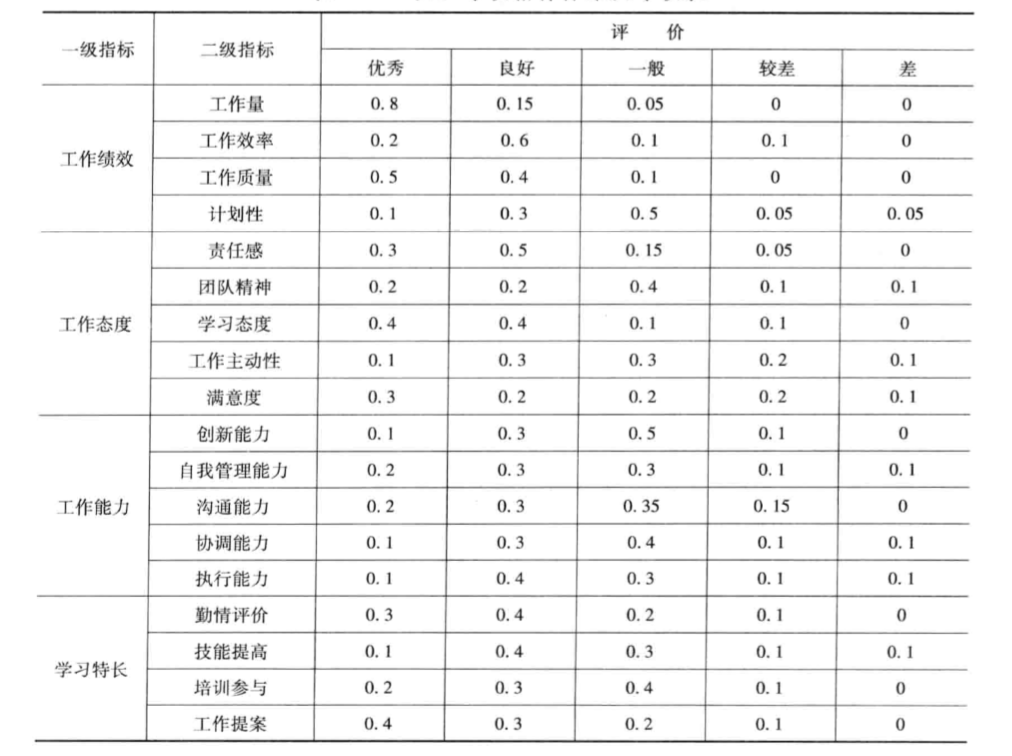
设定一级指标权重和二级指标权重，对各个子因素分别进行一级模糊综合评判，然后再进行二级综合评判；

1. 设专家设定指标权重，一级指标权重为：
   [ A=[0.4,0.3,0.2,0.1] ]
   二级指标权重为：

   

2. 对各个因素进行一级模糊综合评判得到：

   

3. 得到二级评判为：

   

Matlab代码

clc,clear
a=load("data1.txt");
w=[0.4 0.3 0.2 0.1];
w1=[0.2 0.3 0.3 0.2];
w2=[0.3 0.2 0.1 0.2 0.2];
w3=[0.1 0.2 0.3 0.2 0.2];
w4=[0.3 0.2 0.2 0.3];
b(1,:)=w1*a([1:4],:);
b(2,:)=w2*a([5:9],:);
b(3,:)=w3*a([10:14],:);
b(4,:)=w4*a([15:end],:);
c=w*b;
disp(c);

data1.txt

0.8 0.15 0.05 0 0
0.2 0.6 0.1 0.1 0
0.5 0.4 0.1 0 0
0.1 0.3 0.5 0.05 0.05
0.3 0.5 0.15 0.05 0
0.2 0.2 0.4 0.1 0.1
0.4 0.4 0.1 0.1 0
0.1 0.3 0.3 0.2 0.1
0.3 0.2 0.2 0.2 0.1
0.1 0.3 0.5 0.1 0
0.2 0.3 0.3 0.1 0.1
0.2 0.3 0.35 0.15 0
0.1 0.3 0.4 0.1 0.1
0.1 0.4 0.3 0.1 0.1
0.3 0.4 0.2 0.1 0
0.1 0.4 0.3 0.1 0.1
0.2 0.3 0.4 0.1 0
0.4 0.3 0.2 0.1 0