圆锥曲线总结一（椭圆）

Posted 2021-03-09 breadcomplex

椭圆

1. 定义（1）：平面内与两定点(F_1)、(F_2)的距离等于常熟（(2a)>(|F_1F_2|))的点的轨迹叫椭圆。这两定点叫做椭圆的焦点，两焦点间的距离叫做焦距。
   集合(P) = {(M||MF_1|+|MF_2| = 2a，|F_1F_2| = 2c,a>0,c>0,且a,c为常数)}
   定义（2）：在平面内到定点的距离和它到一条定直线的距离之比是个常数(e)，那么这个点的轨迹叫做椭圆。其中定点叫焦点，定直线叫准线，常数e是离心率。
   集合：(P) = {(P|frac{PF}{d} = e)},P为定点，(d)为动点到定直线的距离。
2. 图像
   
   
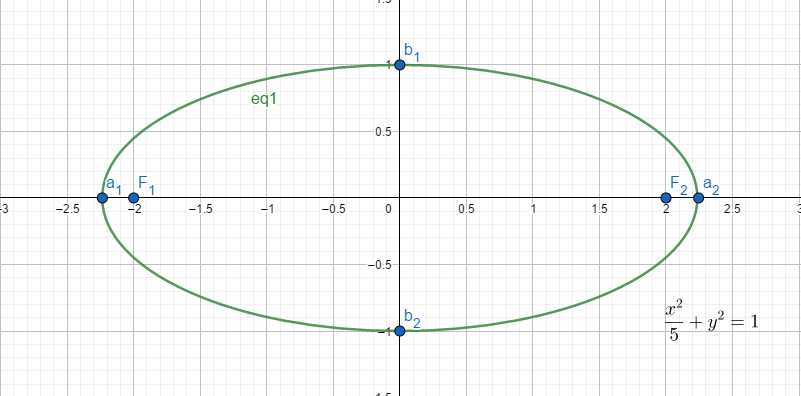
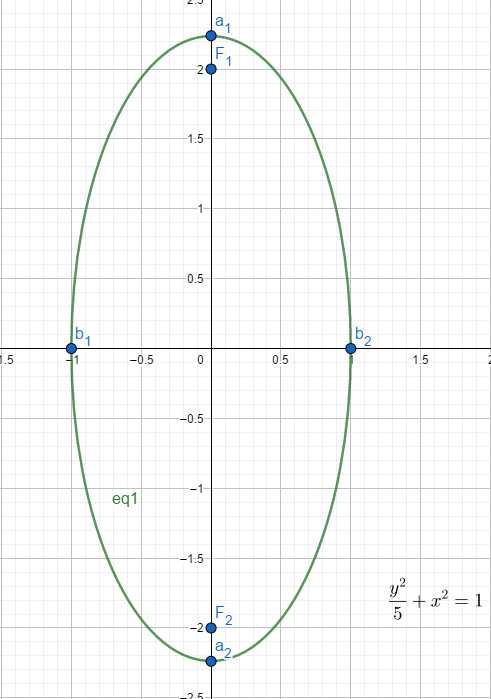
3. 性质
   • 椭圆为轴对称图形，中心对称图形。其对称轴为(x)轴和(y)轴，对称中心为坐标原点。
   • 顶点坐标
     1. 当方程为(frac{x^2}{a^2}+frac{y^2}{b^2}=1)时
        (a_1)：((-a,0)) (a_2)：((a,0)) (b_1)：((0,b)) (b_2)：((0,-b))
     2. 当方程为(frac{y^2}{a^2}+frac{x^2}{b^2}=1)时
        (a_1)：((0,a)) (a_2)：((0,-a)) (b_1)：((-b,0)) (b_2)：((b,0))
   • 焦点坐标
     1. 当方程为(frac{x^2}{a^2}+frac{y^2}{b^2}=1)时
        (F_1:(-c,0)) (F_2:(c,0))
     2. 当方程为(frac{y^2}{a^2}+frac{x^2}{b^2}=1)时
        (F_1:(0,c)) (F_2:(0,-c))
   • (a,b,c)关系
     [c^2 = a^2 - b^2]
   • 离心率
     [e = frac{c}{a} = sqrt{1-(frac{b}{a})^2}hspace{0.5cm}(0 < e < 1)]