搜索（bfs）

Posted 2021-03-09 chen-1

之前，我简略的讲了讲dfs相关的事（见https://www.cnblogs.com/chen-1/p/12328832.html）。

 

接下来，我要简单说一下有关另一种搜索方式——广搜（广度优先搜索），也就是bfs。但首先要明白，bfs与dfs有什么区别。

很明显，它们的搜索方式不同。顾名思义，广搜，是以“广”为搜索顺序的，也就是搜索到一个结点时，会将所有与之相连的

结点都遍历一遍，所以用一个递归的方式来bfs一个图就不太对了。于是用一个队列来储存待遍历的点，可以说是一个等待区，

依次将队列中的点取出并删除，然后将该点所连且未曾入过队的结点都都放入队列尾部，直到队列变空，这样就能实现对全图

的遍历。

 

接下来，可以看一下广搜遍历过程：（假设默认右手法则）

 

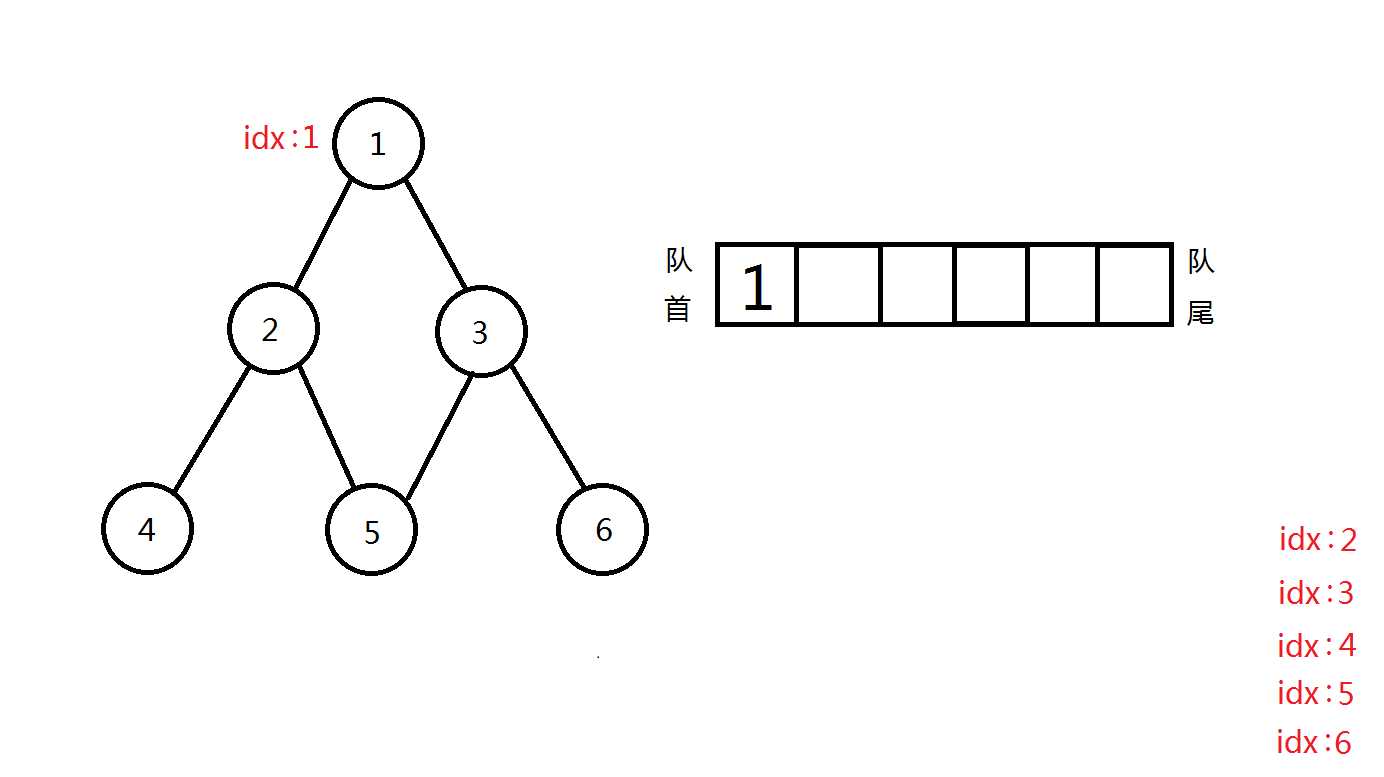
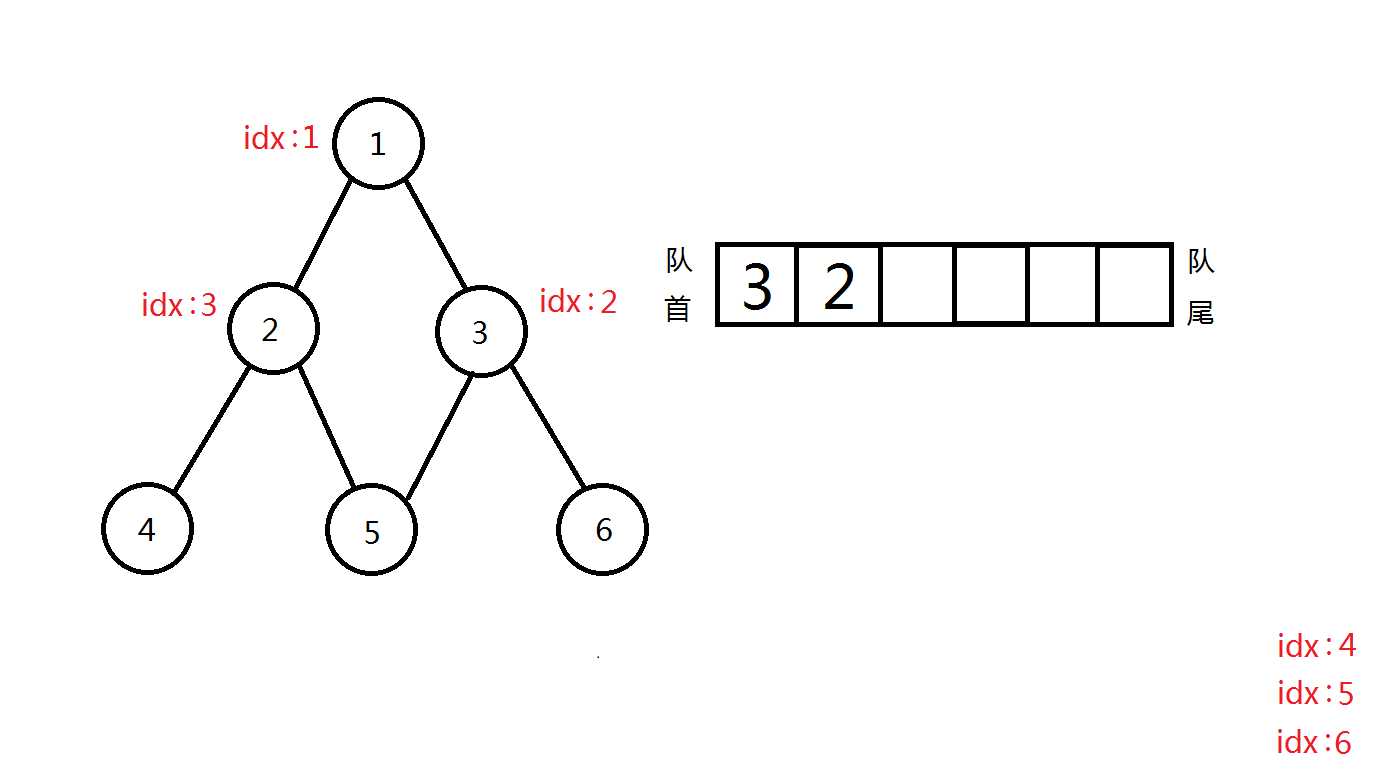
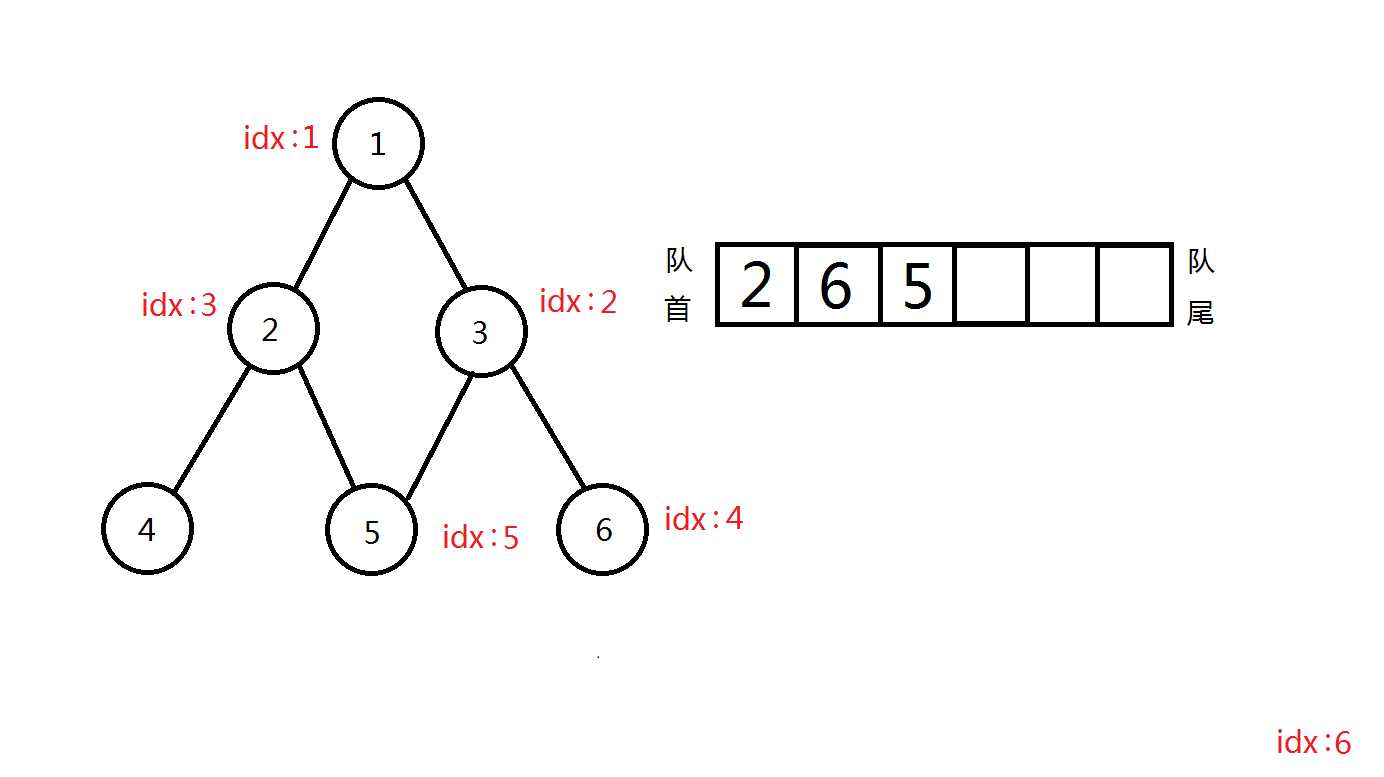
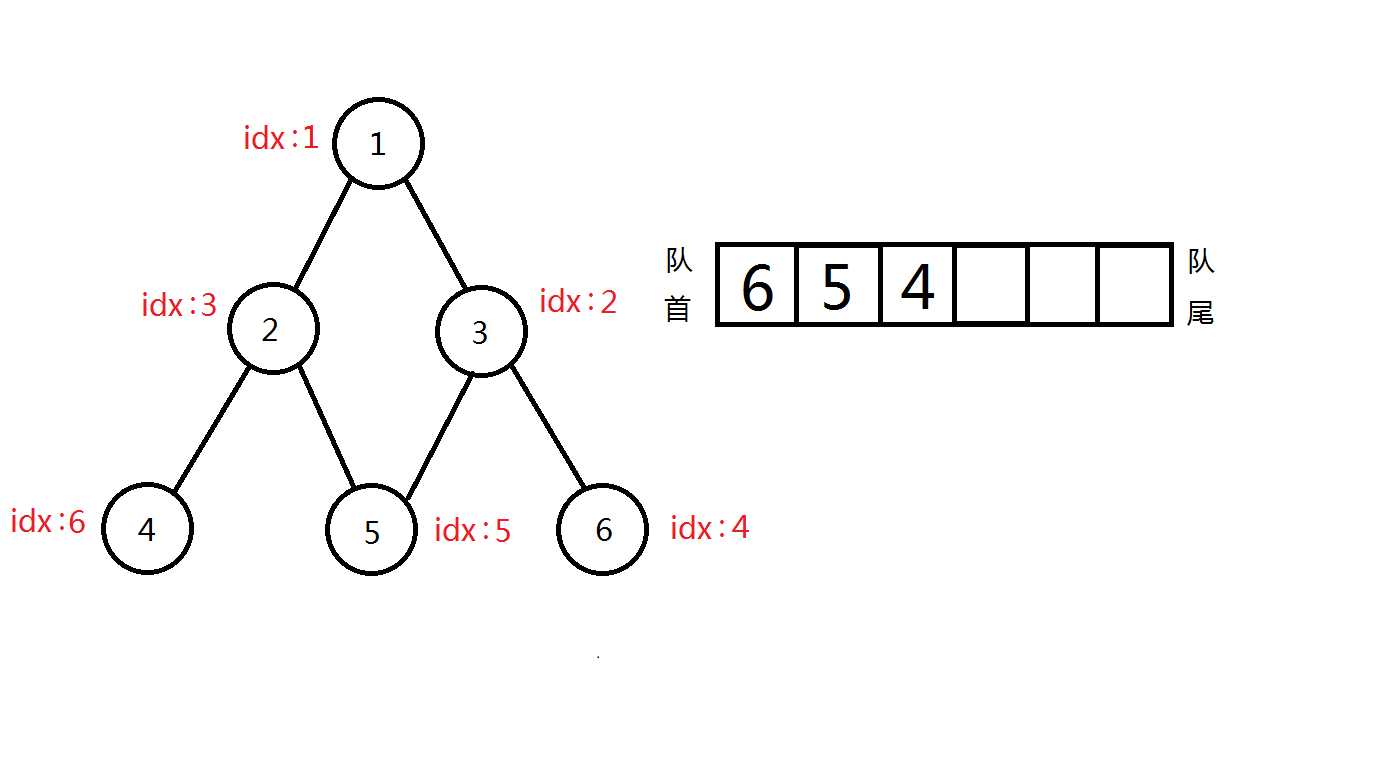
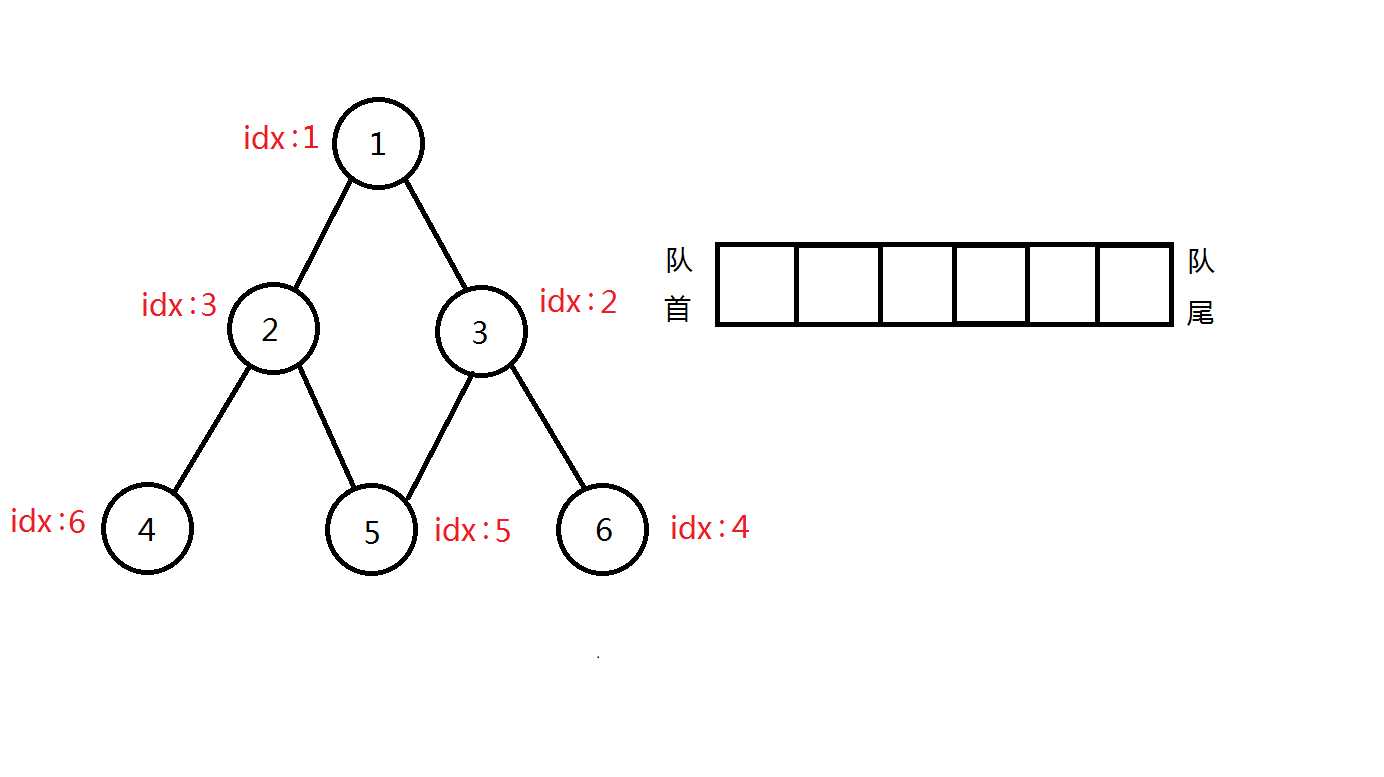
完美完成遍历！

注：广搜适合以其中一个点为起点，求到很多点的路径

 

然后就是广搜经典例题：

https://www.luogu.com.cn/problem/P1443马的遍历

解析：就套用广搜模板，并向8个方向枚举即可。

while(tail>head)
{
    //分别枚举8个方向 
    if(q[head].x+2<=n && q[head].y+1<=m && q[head].x+2>=1 && q[head].y+1>=1 && !flag[q[head].x+2][q[head].y+1])
    {
        //放入队尾 
        q[tail].x=q[head].x+2;
        q[tail].y=q[head].y+1;
        q[tail].num=q[head].num+1;
        flag[q[head].x+2][q[head].y+1]=1;
        tail++;
    }
    if(q[head].x+1<=n && q[head].y+2<=m && q[head].x+1>=1 && q[head].y+2>=1 && !flag[q[head].x+1][q[head].y+2])
    {
        //放入队尾
        q[tail].x=q[head].x+1;
        q[tail].y=q[head].y+2;
        q[tail].num=q[head].num+1;
        flag[q[head].x+1][q[head].y+2]=1;
        tail++;
    }
    if(q[head].x-2<=n && q[head].y-1<=m && q[head].x-2>=1 && q[head].y-1>=1 && !flag[q[head].x-2][q[head].y-1])
    {
        //放入队尾
        q[tail].x=q[head].x-2;
        q[tail].y=q[head].y-1;
        q[tail].num=q[head].num+1;
        flag[q[head].x-2][q[head].y-1]=1;
        tail++;
    }
    if(q[head].x-1<=n && q[head].y-2<=m && q[head].x-1>=1 && q[head].y-2>=1 && !flag[q[head].x-1][q[head].y-2])
    {
        //放入队尾
        q[tail].x=q[head].x-1;
        q[tail].y=q[head].y-2;
        q[tail].num=q[head].num+1;
        flag[q[head].x-1][q[head].y-2]=1;
        tail++;
    }
    if(q[head].x-2<=n && q[head].y+1<=m && q[head].x-2>=1 && q[head].y+1>=1 && !flag[q[head].x-2][q[head].y+1])
    {
        //放入队尾
        q[tail].x=q[head].x-2;
        q[tail].y=q[head].y+1;
        q[tail].num=q[head].num+1;
        flag[q[head].x-2][q[head].y+1]=1;
        tail++;
    }
    if(q[head].x-1<=n && q[head].y+2<=m && q[head].x-1>=1 && q[head].y+2>=1 && !flag[q[head].x-1][q[head].y+2])
    {
        //放入队尾
        q[tail].x=q[head].x-1;
        q[tail].y=q[head].y+2;
        q[tail].num=q[head].num+1;
        flag[q[head].x-1][q[head].y+2]=1;
        tail++;
    }
    if(q[head].x+2<=n && q[head].y-1<=m && q[head].x+2>=1 && q[head].y-1>=1 && !flag[q[head].x+2][q[head].y-1])
    {
        //放入队尾
        q[tail].x=q[head].x+2;
        q[tail].y=q[head].y-1;
        q[tail].num=q[head].num+1;
        flag[q[head].x-2][q[head].y+1]=1;
        tail++;
    }
    if(q[head].x+1<=n && q[head].y-2<=m && q[head].x+1>=1 && q[head].y-2>=1 && !flag[q[head].x+1][q[head].y-2])
    {
        //放入队尾
        q[tail].x=q[head].x+1;
        q[tail].y=q[head].y-2;
        q[tail].num=q[head].num+1;
        flag[q[head].x+1][q[head].y-2]=1;
        tail++;
    }
    //弹出队首 
    head++;
}

 

完整代码：

#include<bits/stdc++.h>
using namespace std;
struct Horse
{
    int x,y;
    int num;    
}q[500*500];
bool flag[501][501];
int head,tail;
int n,m,st1,st2;
int ans[500][500];
int main()
{
    memset(ans,-1,sizeof(ans));
    scanf("%d%d%d%d",&n,&m,&st1,&st2);
    q[1].x=st1,q[1].y=st2,q[1].num=0;
    flag[q[1].x][q[1].y]=1;
    tail=2,head=1;
    while(tail>head)
    {
        if(q[head].x+2<=n && q[head].y+1<=m && q[head].x+2>=1 && q[head].y+1>=1 && !flag[q[head].x+2][q[head].y+1])
        {
            q[tail].x=q[head].x+2;
            q[tail].y=q[head].y+1;
            q[tail].num=q[head].num+1;
            flag[q[head].x+2][q[head].y+1]=1;
            tail++;
        }
        if(q[head].x+1<=n && q[head].y+2<=m && q[head].x+1>=1 && q[head].y+2>=1 && !flag[q[head].x+1][q[head].y+2])
        {
            q[tail].x=q[head].x+1;
            q[tail].y=q[head].y+2;
            q[tail].num=q[head].num+1;
            flag[q[head].x+1][q[head].y+2]=1;
            tail++;
        }
        
        
        if(q[head].x-2<=n && q[head].y-1<=m && q[head].x-2>=1 && q[head].y-1>=1 && !flag[q[head].x-2][q[head].y-1])
        {
            q[tail].x=q[head].x-2;
            q[tail].y=q[head].y-1;
            q[tail].num=q[head].num+1;
            flag[q[head].x-2][q[head].y-1]=1;
            tail++;
        }
        if(q[head].x-1<=n && q[head].y-2<=m && q[head].x-1>=1 && q[head].y-2>=1 && !flag[q[head].x-1][q[head].y-2])
        {
            q[tail].x=q[head].x-1;
            q[tail].y=q[head].y-2;
            q[tail].num=q[head].num+1;
            flag[q[head].x-1][q[head].y-2]=1;
            tail++;
        }
        
        
        if(q[head].x-2<=n && q[head].y+1<=m && q[head].x-2>=1 && q[head].y+1>=1 && !flag[q[head].x-2][q[head].y+1])
        {
            q[tail].x=q[head].x-2;
            q[tail].y=q[head].y+1;
            q[tail].num=q[head].num+1;
            flag[q[head].x-2][q[head].y+1]=1;
            tail++;
        }
        if(q[head].x-1<=n && q[head].y+2<=m && q[head].x-1>=1 && q[head].y+2>=1 && !flag[q[head].x-1][q[head].y+2])
        {
            q[tail].x=q[head].x-1;
            q[tail].y=q[head].y+2;
            q[tail].num=q[head].num+1;
            flag[q[head].x-1][q[head].y+2]=1;
            tail++;
        }
        
        
        if(q[head].x+2<=n && q[head].y-1<=m && q[head].x+2>=1 && q[head].y-1>=1 && !flag[q[head].x+2][q[head].y-1])
        {
            q[tail].x=q[head].x+2;
            q[tail].y=q[head].y-1;
            q[tail].num=q[head].num+1;
            flag[q[head].x-2][q[head].y+1]=1;
            tail++;
        }
        if(q[head].x+1<=n && q[head].y-2<=m && q[head].x+1>=1 && q[head].y-2>=1 && !flag[q[head].x+1][q[head].y-2])
        {
            q[tail].x=q[head].x+1;
            q[tail].y=q[head].y-2;
            q[tail].num=q[head].num+1;
            flag[q[head].x+1][q[head].y-2]=1;
            tail++;
        }
        head++;
    }
    for(int i=1;i<=tail;i++)
    {
        if(ans[q[i].x][q[i].y]>0) ans[q[i].x][q[i].y]=min(q[i].num,ans[q[i].x][q[i].y]);
        else ans[q[i].x][q[i].y]=q[i].num;
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            printf("%-5d",ans[i][j]);
        }
        printf("
");
    }
    return 0;
}

 

最后，还是照例推荐几道较难的题

https://loj.ac/problems/search?keyword=1.4