论线段树

Posted 2020-11-14 yeasio-nein

线段树

首先在这里说明：如果你不知道二叉搜索树是什么的话，请先去学二叉搜索树谢谢。

至于为什么的话，就是因为线段树就是建立在二叉搜索树的基础上。否则可想而知树的遍历会有多复杂，当然，能不能遍历都还不好说。

这里只是对于线段树的一个入门的概念和代码实现过程，至于更高级的操作大多数是是在线段树的一些高级题目中会有涉及。

首先我们举一个例子：（原题：【甩链接】）

告诉你现在有一堆数。哦，就是一堆数列，然后让你维护下面的几个操作：

1.将某一个区间内的每一个数都加上一个x。

2.求出某一个区间内所有数的和。

 

这样，我们先做一组样例来试试看。

1 5 4 2 3.

然后让你进行五组操作：

求2~4的和。

将2~3的所有数加上2。

求3~4的和。

将1~5的所有数加上1。

求1~4的和。

按照暴力出奇迹的思路来看，（并没有什么问题。）这道题不过是单纯的模拟。

嗯，那种时间复杂度为O(不能过)的模拟。

那么在这里我们首先建一个特殊的二叉搜索树。

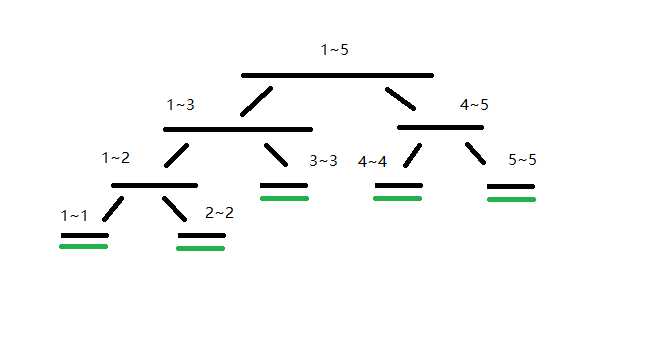
嗯，大家都看到了，这个二叉搜索数的节点就是一个单元区间，而图中标绿的就是其叶子结点，也就是单元区间长度为1的节点。

对于每一个节点，我们定义一个left,一个right，代表左右端点，而当left=right的时候，就是叶子结点了。

借于二叉搜索数的特殊性质,我们知道对一个节点x，他的leftson（左儿子）的编号就是x的编号的两倍，而其rightson（右儿子）的编号就是x的编号的两倍+1.

现在我们来谈一下建数的问题。

首先，对于整个的线段树，我们要有一个struct。当然，结构体的大小是4倍。

struct point
{
    int left;//左端点 
    int right;//右端点 
    int sum;//区间和 
}edge[MAXN*4]; 

其实建树也是一个很简单的操作，就是一个build函数。而在build函数中，主要更新的就是区间和sum。

void build(int left,int right,int now)//now:当前区间的编号 
{
    if(left==right)//到达叶子结点 
    {
        edge[now].sum=value[left];//更新区间和 
        return ;
    }
    int mid=(left+right)/2;//取中间 
    build(left,mid,now*2);
    build(right,mid,now*2+1);
    update(now);//更新操作。 
} 

而其中的那个update(now)就是更新编号为now的节点的区间和sum。很简单，就是将其左子树的sum和右子树的sum加起来。因为这是一个回溯的操作，所以在更新now的sum的时候，其左子树的sum和右子树的sum都已经被更新完毕了。

#define leftson now*2
#define rightson now*2+1
void update(int now)
{
    edge[now].sum=edge[leftson].sum+edge[rightson].sum;
} 

建树完毕了，那么接下来就是区间修改和求和操作了。

在这里我们定义一个lazy tag（懒标记），为什么要定义这个东西呢？按我的话来说，这叫“偷懒延迟”。就是说，当我们接下来要更改的东西不会对下面的操作造成影响的话，我们就可以不去修改它。

也就是说，我们对于将要修改的对象放一个tag，等到下一次又要修改或者询问这个节点的时候，我们才将tag下放给它的子树。

tag的put函数中一共要修改四个元素：

1.左儿子的tag（非左子树）

2.左儿子的sum（非左子树）

3.右儿子的tag（非右子树）

4.右儿子的sum（非右子树）

所以下面就是tag的put函数了：

void put(int now,int mid,int left,int right)
{
    if(tag[now])//如果now节点已经有tag了 
    {//注意tag的put函数只是下放给now节点的左右儿子，而非左右子树 
        tag[leftson]+=tag[now];//为左儿子打tag 
        tag[rightson]+=tag[now];//为右儿子打tag 
        edge[leftson].sum+=(mid-left+1)*tag[now];//更新左儿子
        edge[rightson].sum+=(right-mid+1)*tag[now];//更新右儿子 
        tag[now]=0; //更新完毕，清除tag标记。 
    }
}

 

可以更加形象的理解一下这个lazy tag，就是以为有的修改是对查询没有任何作用的，但是我们又要耗费大量的时间进行修改，于是就会十分两费时间，所以在这里才引入了懒标记，用的时候才进行下放，不用的时候就由你的“爸爸”帮你放着。

当然，上述只是Lazy Tag 的下放而已，区间修改可不能忘了“修改”啊。

void change(int left,int right,int now,int v,int now_left,int now_right)
{
    //v表示要加的数值。 
    //注意：left和righjt是当前找到的节点的左右端点。
    //而now_left 和now_right是查询中要修改的区间的左右端点。 
    if(now_left<=left) 
    if(now_right>right)//如果要修改的区间，完全包含当前节点的区间 
    {
        tag[now]+=v;
        edge[now].sum+=(r-l+1)*v;
        return ;    
    }
    int mid=(l+r)/2;
    put(now,mid,left,right);
    if(now_left<=mid)//继续进行左区间 
    change(left,mid,now*2,v,now_left,now_right);
    if(mid<now_right)//继续进行右区间 
    change(mid,right,now*2+1,v,now_left,now_right); 
    update(now);
} 

 

OK，那么区间修改到此结束，下面是查询。其实看完了上面这些之后查询反而变成了最简单的事情了。

直接借鉴上面change就好。

int ask(int left,int right,int now,int now_left,int now_right)
{
    //注意：left和righjt是当前找到的节点的左右端点。
    //而now_left 和now_right是查询中的区间的左右端点。 
    int ans;
    if(now_left<=left)//完全包含 
    if(now_right>right)
    return edge[now].sum; //直接返回当前节点的值就好。 
    int mid=(left+right)/2;//取中间 
    put(now,mid,left,right);//下放标记 
    if(mid>now_left) //更新左边 
    ans+=find(left,mid,now*2,now_left,now_right);
    if(mid<now_right) //更新右边 
    ans+=find(mid,right,now*2+1,now_left,now_right);
    return ans;//返回答案 
} 

好，最基本的线段树到此先告一段落。

因为这只是最基本的线段树操作，如果想学习更高深的一些算法还要多家联系才行。

（该博客的代码完全现场手打，可能有误，请读者尽量不要照抄）

（由于各种原因，没有放上全部code，如果有需要在下方回复"Need Code"就好，我会尽快添加代码）

——Yeasion_Nein