数据结构与算法----散列/哈希

Posted 2021-03-09 taoxiang

1. 简介

　　散列表的实现叫散列hashing，散列用于以常数平均时间执行 插入、删除、查找，不支持排序、findMin、findMax。

　　查找关键字不需要 比较

　　在一个记录的存储位置和它的关键字之间建立映射关系：key--f(key)   这个关系就是散列函数/哈希函数。将一些记录存储在一块 连续 的存储空间，这块空间就是散列表/哈希表。

 

　　与线性表、树、图比较：

　　　　数据元素之间没有什么逻辑关系，也不能用连线图表示出来。

 

　　问题：

　　　　关键字不同，但通过散列函数计算的结果相同，即出现了冲突 collision，这两个关键字就是这个散列函数的同义词 synonym

 

2. 散列函数

  2.1 设计原则

　　计算简单

　　散列地址分布均匀

 

  2.2 

　　计算散列地址所需时间

　　关键字长度

　　散列表大小

　　关键字分布情况

　　记录查找的频率

 

  2.3 常用方法

（1）直接定址

　　线性函数：f(key) = a*key + b （a、b为常数）

　　特点：简单、均匀

　　适合：要实现知道关键字的分布情况，适合表较小且连续的情况

 

（2）数字分析

　　根据关键字特点，抽取关键字的一部分来计算散列存储位置

　　适合：关键字位数比较大，事先知道关键字的分布且关键字的若干位分布均匀

 

（3）平方取中

　　关键字平方，再取中间的几位

　　适合：不知道关键字的分布，而位数不大的情况

 

（4）折叠法

　　将关键字从左到右分割成位数相等的几部分，再将这几部分叠加求和，并按散列表表长取后几位作为散列地址

　　例：散列表长3位，关键字9876543210

　　　　将关键字分成四组，叠加求和987+654+321+0=1962   取后3位 962 作为散列地址

　　　　不够均匀的话，可折叠某几个数再叠加：789+654+123+0=1566 取566作为散列地址

 

　　适合：不知道关键字的分布，位数较多

 

（5）除留余数法

　　已知散列表长为m， f(key) = key mod p (p≤m)

　　也可以先对key折叠、平方取中等之后再除留余数

　　p的选择：小于等于表长的最小质数 或 不包含小于20质因子的合数

 

（6）随机数法

　　f(key) = random(key) 

　　适合关键字长度不等的情况

　　关键字是字符串时：转化为数字，如ASCII码、Unicode码

 

3. 处理散列冲突

（1）开放定址法/线性探测法

　　当发生了冲突的时候就去寻找下一个空的散列地址，只要散列表够大，总能找到空的散列地址。

　　　　f_i(key) = (f(key) + d_i) mod m     (d_i=1,2...m-1)

　　问题：key2因为与key1冲突，找到空的散列地址存储数据，但是key3本来和key2不是同义词，key3的位置却被key2占了，所以又需要为key3再找位置，甚至可能导致冲突不断出现。即出来了堆积。

　　不足：当前散列函数只能在冲突发生时往下一个地址寻址，不能往前，因此可让 d_i 为负值，并且让步进的间隔大点，不让关键字聚集在某一块区域。

　　改进：二次探测法

　　　　fi(key) = (f(key) + di) mod m   (di=1²,-1²,2²,-2²...q²,-q²   q≤m/2)

　　　　

　　另一种：d_i用随机函数计算得到------随机探测法

　　

　　特点：在散列表未满时，总能找到不发生冲突的地址

 

（2）再散列函数法

　　当发生冲突时，就换一个散列函数计算

 

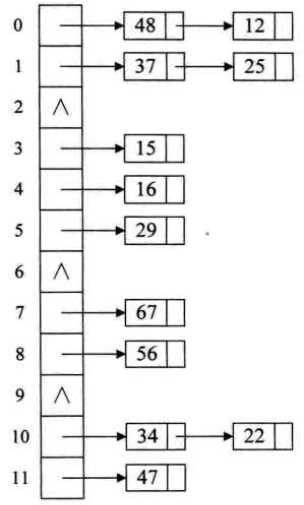
（3）链地址法

　　发生冲突时，不换地方存储，而是在原地址用链表存储。即将所有关键字为同义词的记录存储在一个链表中。

                       

 

 

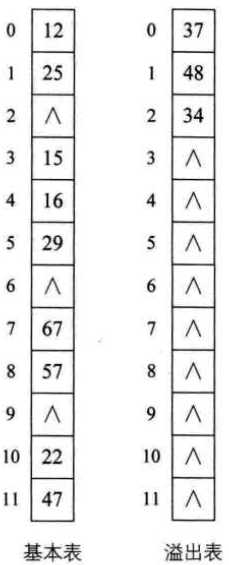
（4）公共溢出区法

　　为所有冲突的关键字建立一个公共的溢出区存放。

              　　

 

 

4. 装填因子α

　　α=填入表中的记录个数/散列表长度

　　装填因子越大，产生冲突的可能性就越大。

 

　　不产生冲突时，查找的时间复杂度为O(1)

 

5. 散列表的简单实现

  《大话数据结构》里面的代码

#define HASHSIZE 12
typedef struct {
    int *elem;
    int count; //当前数据元素个数
}MyHashTable;

 

  初始化：

bool initHashTable(MyHashTable *h)
{
    h->count = 0;
    h->elem = (int *)malloc(HASHSIZE*sizeof(int));
    for(int i=0;i<HASHSIZE;i++) {
        h->elem[i] = -32768;
    }
    return true;
}

 

  散列函数：

static int MyHash(int key)
{
    return key % HASHSIZE;
}

 

  插入元素：

void insertHash(MyHashTable *h,int key)
{
    int addr = MyHash(key);  //求得散列地址
    while(h->elem[addr] != -32768) {
        addr = (addr+1) % HASHSIZE; //开放定址法的线性探测
    }
    h->elem[addr] = key;
    (h->count)++;
}

 

  查找：

int searchHash(MyHashTable h,int key,int *addr)
{
    *addr = MyHash(key);
    while(h.elem[*addr] != key) {   //当找到了这个key则退出循环
        *addr = (*addr + 1) % HASHSIZE;
        if(*addr == MyHash(key)) {
            //循环到了原来的地方  说明整个表里没有这个key
            return -1;
        }
    }
    return *addr;
}