ML-6-2集成学习-boosting（Adaboost和GBDT ）

Posted 2021-03-08 yifanrensheng

目录

1. 简述集成学习
2. Boosting介绍
3. AdaBoost算法
4. GBDT算法
5. 总结

一、简述集成学习

上一篇博文已经介绍了：集成算法是由多个弱学习器组成的算法，根据个体学习器的生成方式不同，集成算法分成两类：

1. 个体学习器之间不存在强依赖关系，可以并行化生成每个个体学习器，这一类的代表是Bagging（常见的算法有RandomForest）。
2. 个体学习器之间存在强依赖关系，必须串行化生成的序列化方法，这一类的代表是Boosting（常见的算法有Adaboost、GBDT）；

　本文只介绍第一类：Boosting（常见的算法有Adaboost、GBDT）

二、Boosting介绍

在随机森林的构建过程中，由于各棵树之间是没有关系，相对独立的；在构建的过程中，构建第m棵子树的时候，不会考虑前面的m-1棵树。

思考：

1. 如果在构建第m棵子树的时候，考虑到前m-1棵子树的结果，会不会对最终结果产生有益的影响？
2. 各个决策树组成随机森林后，在形成最终结果的时候能不能给定一种既定的决策顺序呢？(也就是哪棵子树先进行决策、哪棵子树后进行决策)

这个问题引出了Boosting的学习算法

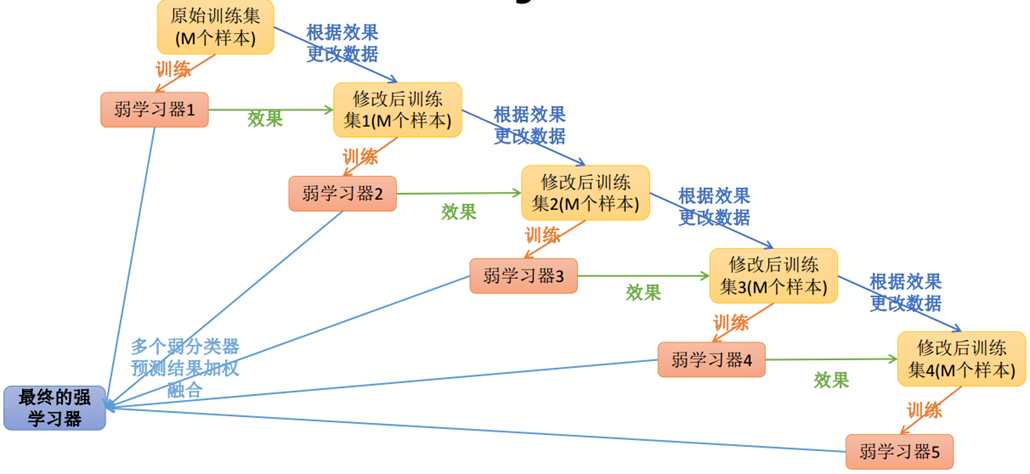
提升学习（Boosting）是一种机器学习技术，可以用于回归和分类的问题，它每一步产生弱预测模型(如决策树)，并加权累加到总模型中；如果每一步的弱预测模型的生成都是依据损失函数的梯度方式的，那么就称为梯度提升(Gradient boosting)；

提升技术的意义：如果一个问题存在弱预测模型，那么可以通过提升技术的办法得到一个强预测模型；

有几个具体的问题Boosting算法没有详细说明。

1. 如何计算学习误差率e?
2. 如何得到弱学习器权重系数α?
3. 如何更新样本权重D?
4. 使用何种结合策略？

只要是boosting大家族的算法，都要解决这4个问题。

三、AdaBoost算法

3.1 AdaBoost算法原理

Adaptive Boosting是一种迭代算法。每轮迭代中会在训练集上产生一个新的学习器，然后使用该学习器对所有样本进行预测，以评估每个样本的重要性(Informative)。换句话来讲就是，算法会为每个样本赋予一个权重，每次用训练好的学习器标注/预测各个样本，如果某个样本点被预测的越正确，则将其权重降低；否则提高样本的权重。权重越高的样本在下一个迭代训练中所占的比重就越大，也就是说越难区分的样本在训练过程中会变得越重要；

整个迭代过程直到错误率足够小或者达到一定的迭代次数为止。Adaboost算法将基分类器的线性组合作为强分类器，同时给分类误差率较小的基本分类器以大的权值，给分类误差率较大的基分类器以小的权重值；构建的线性组合为：

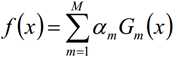
最终分类器是在线性组合的基础上进行Sign函数转换：

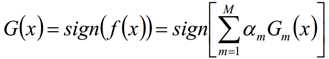
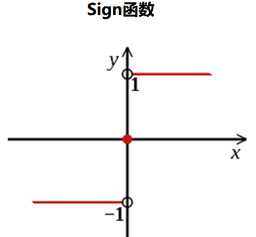
最终的强学习器：

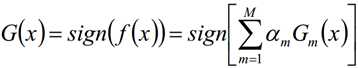
损失函数：

第k-1轮的强学习器：

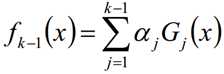
第k轮的强学习器：

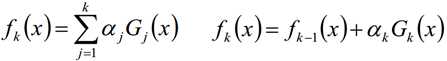
损失函数：

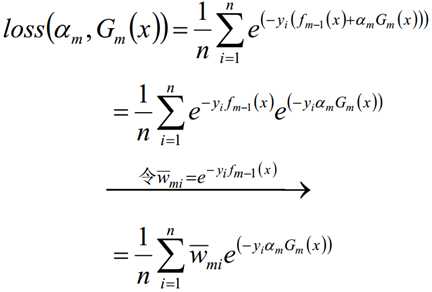
使下列公式达到最小值的αm和Gm就是AdaBoost算法的最终求解值

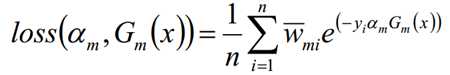
G这个分类器在训练的过程中，是为了让误差率最小，所以可以认为G越小其实就是误差率越小

对于αm而言，通过求导然后令导数为零，可以得到公式（log对象可以以e为底也可以以2为底）:

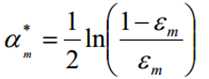
3.2 AdaBoost算法过程

3.3 AdaBoost算法案例

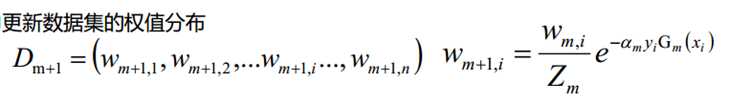
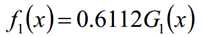
分类器sign(f1(x))在训练数据集上有3个误分类点

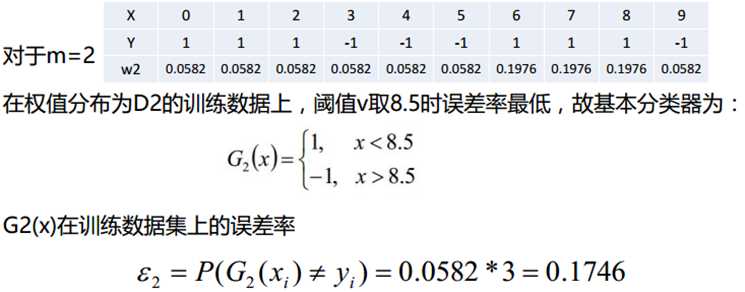
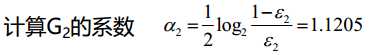
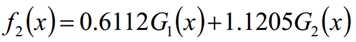
分类器sign(f2(x))在训练数据集上有3个误分类点

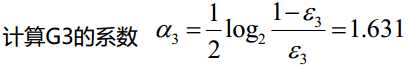
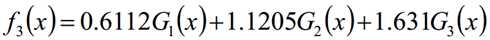
分类器sign(f3(x))在训练数据集上有0个误分类点；结束循环

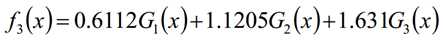
3.4 AdaBoost总结

AdaBoost的优点：

1. 可以处理连续值和离散值；
2. 模型的鲁棒性比较强；
3. 解释强，结构简单。

AdaBoost的缺点：

1. 对异常样本敏感，异常样本可能会在迭代过程中获得较高的权重值，最终影响模型效果。

四、GBDT算法

4.1 GBDT算法原理

　　GBDT是梯度提升决策树（Gradient Boosting Decision Tree）的简称，GBDT可以说是最好的机器学习算法之一。GBDT也是Boosting算法的一种，但是和AdaBoost算法不同；区别如下：AdaBoost算法是利用前一轮的弱学习器的误差来更新样本权重值，然后一轮一轮的迭代；GBDT也是迭代，但是GBDT要求弱学习器必须是CART模型，而且GBDT在模型训练的时候，是要求模型预测的样本损失尽可能的小。

用于一个简单的例子来说明GBDT，假如某人的年龄为30岁，第一次用20岁去拟合，发现损失还有10岁，第二次用6岁去拟合10岁，发现损失还有4岁，第三次用3岁去拟合4岁，依次下去直到损失在我们可接受范围内。

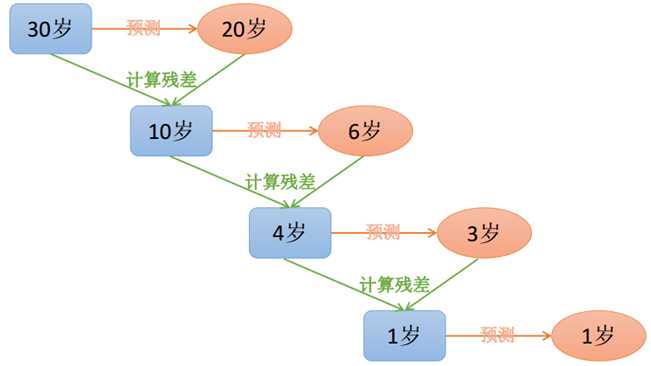
4.2 GBDT算法过程

给定输入向量X和输出变量Y组成的若干训练样本(X1,Y1),(X2,Y2)......(Xn,Yn)，目标是找到近似函数F(X)，使得损失函数L(Y,F(X))的损失值最小。

L损失函数一般采用最小二乘损失函数或者绝对值损失函数

采用前向分布算法

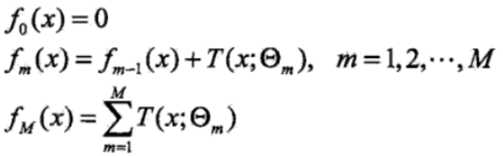
在第m次迭代时，我们要优化的损失函数：

损失函数变为：

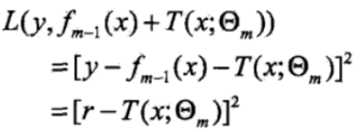
问题就成了对残差r的拟合了

然而对于大多数损失函数，却没那么容易直接获得模型的残差，针对该问题，大神Freidman提出了用损失函数的负梯度来拟合本轮损失的近似值，拟合一个回归树

1）初始化f0(x)：

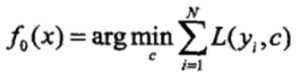
2）第m次迭代时，计算当前要拟合的残差rmi：

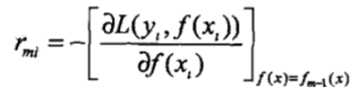
以rmi为输出值，对rmi拟合一个回归树（此时只是确定了树的结构，但是还未确定叶子节点中的输出值），然后通过最小化当前的损失函数，并求得每个叶子节点中的输出值cmj，j表示第j个叶子节点

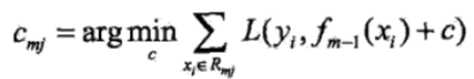
更新当前的模型fm(x)为：

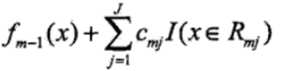
3）依次迭代到我们设定的基学习器的个数M，得到最终的模型，其中M表示基学习器的个数，JJ表示叶子节点的个数

　　GBDT算法提供了众多的可选择的损失函数，通过选择不同的损失函数可以用来处理分类、回归问题，比如用对数似然损失函数就可以处理分类问题。大概的总结下常用的损失函数：

1. 对于分类问题可以选用指数损失函数、对数损失函数。
2. 对于回归问题可以选用均方差损失函数、绝对损失函数。
3. 另外还有huber损失函数和分位数损失函数，也是用于回归问题，可以增加回归问题的健壮性，可以减少异常点对损失函数的影响。

4.3GBDT的正则化

　　在Adaboost中我们会对每个模型乘上一个弱化系数（正则化系数），减小每个模型对提升的贡献（注意：这个系数和模型的权重不一样，是在权重上又乘以一个0,1之间的小数），在GBDT中我们采用同样的策略，对于每个模型乘以一个系数λ (0 < λ ≤ 1)，降低每个模型对拟合损失的贡献，这种方法也意味着我们需要更多的基学习器。

　　第二种是每次通过按比例（推荐[0.5, 0.8] 之间）随机抽取部分样本来训练模型，这种方法有点类似Bagging，可以减小方差，但同样会增加模型的偏差，可采用交叉验证选取，这种方式称为子采样。采用子采样的GBDT有时也称为随机梯度提升树（SGBT）。

　　第三种就是控制基学习器CART树的复杂度，可以采用剪枝正则化。

4.4 GBDT的优缺点

GBDT的主要优点：

1. 可以灵活的处理各种类型的数据
2. 预测的准确率高
3. 使用了一些健壮的损失函数，如huber，可以很好的处理异常值

GBDT的缺点：

由于基学习器之间的依赖关系，难以并行化处理，不过可以通过子采样的SGBT来实现部分并行。

五、比较总结

5.1 迭代决策树和随机森林的区别：

1. 随机森林使用抽取不同的样本构建不同的子树，也就是说第m棵树的构建和前m-1棵树的结果是没有关系的
2. 迭代决策树在构建子树的时候，使用之前子树构建结果后形成的残差作为输入数据构建下一个子树；然后最终预测的时候按照子树构建的顺序进行预测，并将预测结果相加

5.2 Adaboost和GBDT的区别：

1. Adaboost思想是通过决策树调整数据权重，找到对误分类的数据准确度更高的模型，因为此时误分类的数据权重高。最终是将所有的模型加权结合来找到准确率更高的模型。
2. GBDT的思想是一步步缩小估计值与模型的误差，新的模型训练数据的误差，数据权值没有什么变化。

5.3 Bagging和Boosting的区别：

1）样本选择上：

　　Bagging：训练集是在原始集中有放回选取的，从原始集中选出的各轮训练集之间是独立的。

　　Boosting：每一轮的训练集不变，只是训练集中每个样例在分类器中的权重发生变化。而权值是根据上一轮的分类结果进行调整。

2）样例权重：

　　Bagging：使用均匀取样，每个样例的权重相等

　　Boosting：根据错误率不断调整样例的权值，错误率越大则权重越大。

3）预测函数：

　　Bagging：所有预测函数的权重相等。

　　Boosting：每个弱分类器都有相应的权重，对于分类误差小的分类器会有更大的权重。

4）并行计算：

　　Bagging：各个预测函数可以并行生成

　　Boosting：各个预测函数只能顺序生成，因为后一个模型参数需要前一轮模型的结果。　

说明：决策树与这些算法框架进行结合所得到的新的算法：

　　1）Bagging + 决策树 = 随机森林

　　2）AdaBoost + 决策树 = 提升树

　　3）Gradient Boosting + 决策树 = GBDT

附件一：AdaBoost scikit-learn相关参数

附件二：GBDT scikit-learn相关参数

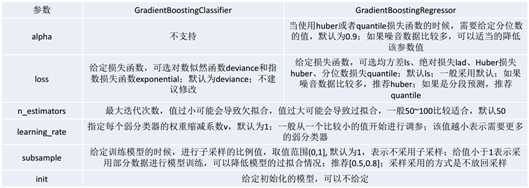
附件三：集成学习的组合方法

① 投票法

投票法是用于分类问题，由多个学习器投票，哪个类别最多就是哪个。所谓的少数服从多数，如果出现数量相同，那就在相同中随机选择一个；

升级版：

绝对多数投票法，在相对多数投票结果基础上，还要过半才算有效；

加权投票法：赋予不同学习器不同的权重，再加权求和

② 平均法

平均法用于回归预测问题，对学习器的结果求算法平均，得到最终的预测结果

升级版：加权求和

③ stack法

上2个方法都是对弱学习器的结果做平均或者投票，相对比较简单，但是可能学习误差较大，于是就有了学习法这种方法，代表方法是stacking。

当使用stacking的结合策略时， 我们不是对弱学习器的结果做简单的逻辑处理，而是再加上一层学习器，也就是说，我们将训练集弱学习器的学习结果作为输入，将训练集的输出作为输出，重新训练一个学习器来得到最终结果。

在这种情况下，我们将弱学习器称为初级学习器，将用于结合的学习器称为次级学习器。对于测试集，我们首先用初级学习器预测一次，得到次级学习器的输入样本，再用次级学习器预测一次，得到最终的预测结果。

附件三：Adaboost算法

 

# Author:yifan
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
from sklearn.ensemble import AdaBoostClassifier#adaboost引入方法
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import make_gaussian_quantiles#造数据

## 设置属性防止中文乱码
mpl.rcParams[‘font.sans-serif‘] = [u‘SimHei‘]
mpl.rcParams[‘axes.unicode_minus‘] = False

## 创建数据
X1, y1 = make_gaussian_quantiles(cov=2.,n_samples=200, n_features=2,n_classes=2, random_state=1)#创建符合高斯分布的数据集
X2, y2 = make_gaussian_quantiles(mean=(3, 3), cov=1.5, n_samples=300, n_features=2, n_classes=2, random_state=1)
X = np.concatenate((X1, X2))
y = np.concatenate((y1, - y2 + 1))
#构建adaboost模型
bdt = AdaBoostClassifier(DecisionTreeClassifier(max_depth=1),
                         algorithm="SAMME.R",#可以不写
                         n_estimators=200)
#数据量大的时候，可以增加内部分类器的树深度，也可以不限制树深
#max_depth树深，数据量大的时候，一般范围在10——100之间，数据量小的时候，一般可以设置树深度较小，或者n_estimators较小
#n_estimators 迭代次数或者最大弱分类器数：200次
#base_estimator：DecisionTreeClassifier 选择弱分类器，默认为CART树
#algorithm：SAMME 和SAMME.R 。运算规则，后者是优化算法，以概率调整权重，迭代速度快，
#需要能计算概率的分类器支持
#learning_rate：0<v<=1，默认为1，正则项 衰减指数
#loss：linear、‘square’exponential’。误差计算公式：一般用linear足够
bdt.fit(X, y)

plot_step = 0.02
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, plot_step), np.arange(y_min, y_max, plot_step))
#预测
Z = bdt.predict(np.c_[xx.ravel(), yy.ravel()])
#设置维度
Z = Z.reshape(xx.shape)

## 画图
plot_colors = "br"
class_names = "AB"

plt.figure(figsize=(10, 5), facecolor=‘w‘)
#局部子图
plt.subplot(121)
plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired)
for i, n, c in zip(range(2), class_names, plot_colors):
    idx = np.where(y == i)
    plt.scatter(X[idx, 0], X[idx, 1],
                c=c, cmap=plt.cm.Paired,
                label=u"类别%s" % n)
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.legend(loc=‘upper right‘)
plt.xlabel(‘x‘)
plt.ylabel(‘y‘)
plt.title(u‘AdaBoost分类结果,正确率为:%.2f%%‘ % (bdt.score(X, y) * 100))

#获取决策函数的数值
twoclass_output = bdt.decision_function(X)
#获取范围
plot_range = (twoclass_output.min(), twoclass_output.max())
plt.subplot(122)
for i, n, c in zip(range(2), class_names, plot_colors):
#直方图
    plt.hist(twoclass_output[y == i],
             bins=20,
             range=plot_range,
             facecolor=c,
             label=u‘类别 %s‘ % n,
             alpha=.5)
x1, x2, y1, y2 = plt.axis()
plt.axis((x1, x2, y1, y2 * 1.2))
plt.legend(loc=‘upper right‘)
plt.ylabel(u‘样本数‘)
plt.xlabel(u‘决策函数值‘)
plt.title(u‘AdaBoost的决策值‘)

plt.tight_layout()
plt.subplots_adjust(wspace=0.35)
plt.show()

　　

   

附件四：手写推导过程练习