马尔科夫链蒙特卡洛采样（MCMC）入门

Posted 2021-03-07 emanlee

1、从随机变量分布中采样

研究人员提出的概率模型对于分析方法来说往往过于复杂。越来越多的研究人员依赖数学计算的方法处理复杂的概率模型，研究者通过使用计算的方法，摆脱一些分析技术所需要的不切实际的假设。（如，正态和独立）

大多数近似方法的关键是在于从分布中采样的能力，我们需要通过采样来预测特定的模型在某些情况下的行为，并为潜在的变量（参数）找到合适的值以及将模型应用到实验数据中，大多数采样方法都是将复杂的分布中抽样的问题转化到简单子问题的采样分布中。

本章，我们解释两种采样方法：逆变换方法（the inverse transformation method）和拒绝采样（rejection sampling）。这些方法主要适用于单变量的情况，用于处理输出单变量的问题。在下一章，我们讨论马尔科夫链蒙特卡洛方法（Markov chain Monte Carlo），该方法可以有效的用于多元变量分布采样。

 

1.1 标准分布

有一些分布被经常用到，这些分布被MATLAB作为标准分布实现。在MATLAB统计工具箱（Matlab Statistics Toolbox supports）实现了一系列概率分布。使用MATLAB工具箱可以很方便的计算这些分布的概率密度、累积密度、并从这些分布中取样随机值。表1.1列举了一些MATLAB工具箱中的标准分布。在MATLAB文档中列举了更多的分布，这些分布可以用MATLAB模拟。利用在线资源，通常很容易能找到对其他常见分布的支持。

 

 

 

 

 

 

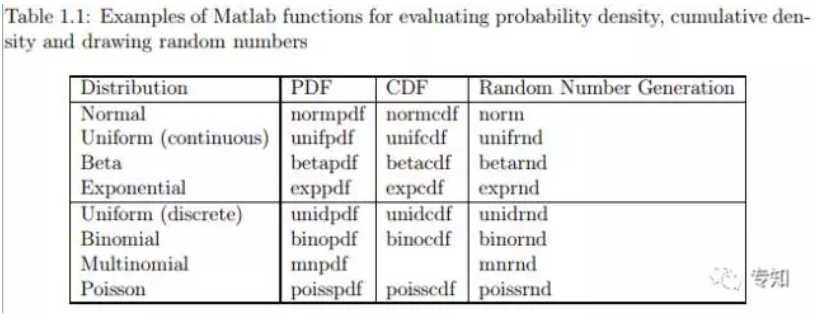
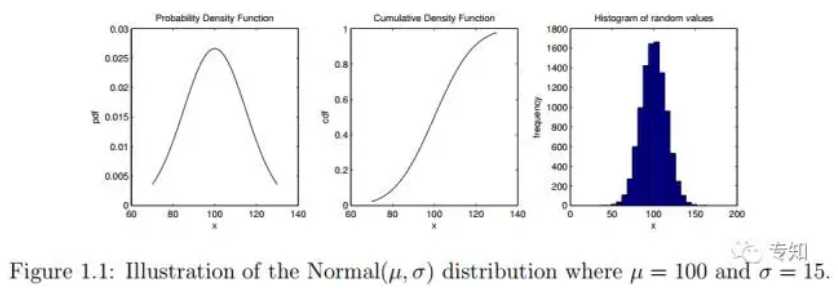
 为了说明如何使用这些函数，Listing 1.1展示了正态分布N(μ,σ)可视化的MATLAB代码，其中μ=100,σ=15。

举例

举个例子，可以想象一下用该正态分布表示观察到的人群的IQ系数变化。该代码显示了了如何展示概率密度和累积密度。它还展示了如何从该分布中抽取随机值以及如何使用hist函数可视化这些随机样本。代码的输出结果如图1.1所示。类似的，图1.2可视化离散的二项分布Binomial(N,θ)，其中参数N=10,θ=0.7。该分布可认为是进行10次实验，每次试验成功的概率是θ=0.7。

 %% Explore the Normal distribution N( mu , sigma )
 mu = 100; % the mean
 sigma = 15; % the standard deviation
 xmin = 70; % minimum x value for pdf and cdf plot
 xmax = 130; % maximum x value for pdf and cdf plot
 n = 100; % number of points on pdf and cdf plot
 k = 10000; % number of random draws for histogram

 % create a set of values ranging from xmin to xmax
 x = linspace( xmin , xmax , n );
 p = normpdf( x , mu , sigma ); % calculate the pdf
 c = normcdf( x , mu , sigma ); % calculate the cdf

 figure( 1 ); clf; % create a new figure and clear the contents

 subplot( 1,3,1 );
 plot( x , p , ‘k?‘ );
 xlabel( ‘x‘ ); ylabel( ‘pdf‘ );
 title( ‘Probability Density Function‘ );

 subplot( 1,3,2 );
 plot( x , c , ‘k?‘ );
 xlabel( ‘x‘ ); ylabel( ‘cdf‘ );
 title( ‘Cumulative Density Function‘ );

 % draw k random numbers from a N( mu , sigma ) distribution
 y = normrnd( mu , sigma , k , 1 );

 subplot( 1,3,3 );
 hist( y , 20 );
 xlabel( ‘x‘ ); ylabel( ‘frequency‘ );
 title( ‘Histogram of random values‘ );

 

Listing 1.1: Matlab code to visualize Normal distribution.

 

1.2 从非标准分布中采样

我们希望MATLAB工具也支持从非标准分布中采样，这种情况在建模过程中经常出现，因为研究人员可以提出一种新的噪声过程或已存在分布的组合方式。复杂采样问题的计算方法通常依赖于我们已经知道如何有效地进行采样的分布。这些从简单分布中采样的随机值可以被转换成目标分布需要的值。事实上，这一节我们讨论的一些技术是MATLAB的内部分布，如正态分布和指数分布。

1.2.1 用离散变量进行逆变换采样（Inverse transform sampling）

逆变换采样（也被成为逆变换方法）即给定累积分布函数的逆，可从任意概率分布中生成随机数。这个方法是对均匀分布的随机数字进行采样（在0到1之间）然后使用逆累积分布函数转换这些值。该过程的简单之处就在于，潜在的采样仅仅依赖对统一的参数进行偏移和变换。该过程可以用于采样很多不同种类的分布，事实上，MATLAB实现很多随机变量生成方法也是基于该方法的。

在离散分布中，我们知道每个输出结果的概率。这种情况下，逆变换方法就需要一个简单的查找表。

给定一个非标准的离散分布的例子，我们使用一些实验数据来研究人类如何能产生一致的随机数（如Treisman and Faulkner,1987）。在这些实验中，被测试者会产生大量的随机数字（0,…,9）。研究人员根据每个随机数字的相对频率进行制表。你可能会怀疑实验对象不会总是产生均匀分布。表1.2.1展示了一些典型的数据，其中可以看出一些比较低的和高的数字容易被忽视，而一些特殊数字（如数字4）占过高的比例。由于某种原因，数字0和9从来没有被产生。在任何情况下，这些数字都是相当典型的，而且证明了人类不能很好地产生均匀分布的随机数字。

 

 

From:

https://mp.weixin.qq.com/s?__biz=MzU2OTA0NzE2NA==&mid=2247483828&idx=1&sn=24dc135cf0d45a1dd276c0247c3e99d4&chksm=fc85e0a7cbf269b1b368465431e8050f1591f8d5611a923de92d999aed47abd8ce5cb0367142&scene=21#wechat_redirect