KNN 和K-means

Posted 2021-03-07 antoniosu

一、KNN

　　KNN是一种分类算法，它不具有显式的学习过程。对应的输入是特征空间的点，输出为实例的类别，可以是多类别。

1.算法思路

　　如果一个样本在特征空间中的k个最邻近的样本中的大多数属于某一个类别，则该样本也划分为这个类别。KNN算法中，所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。

举例说明如下：

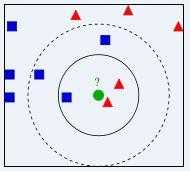
　　我们要确定绿点属于哪个颜色（红色或者蓝色），要做的就是选出距离目标点距离最近的k个点，看这k个点的大多数颜色是什么颜色。当k取3的时候，我们可以看出距离最近的三个，分别是红色、红色、蓝色，因此得到目标点为红色。

 

算法步骤：

　　1）计算测试数据与各个训练数据之间的距离；

　　2）按照距离的递增关系进行排序；

　　3）选取距离最小的K个点；

　　4）确定前K个点所在类别的出现频率；

　　5）返回前K个点中出现频率最高的类别作为测试数据的预测分类

2.三个基本要素

• k值的选择：k值的选择会对结果产生重大影响。较小的k值可以减少近似误差(训练集误差)，但是会增加估计误差(测试误差)；较大的k值可以减小估计误差，但是会增加近似误差。
• 距离度量：距离反映了特征空间中两个实例的相似程度。可以采用欧氏距离、曼哈顿距离等。
• 分类决策规则：往往采用多数表决。

3.关于K的取值

　　K值得选取非常重要，因为：

　　如果当K的取值过小时，一旦有噪声得成分存在们将会对预测产生比较大影响，例如取K值为1时，一旦最近的一个点是噪声，那么就会出现偏差，K值的减小就意味着整体模型变得复杂，容易发生过拟合；

　　如果K的值取的过大时，就相当于用较大邻域中的训练实例进行预测，学习的近似误差会增大。这时与输入目标点较远实例也会对预测起作用，使预测发生错误。K值的增大就意味着整体的模型变得简单；

　　如果K==N的时候，那么就是取全部的实例，即为取实例中某分类下最多的点，就对预测没有什么实际的意义了；

　　K的取值尽量要取奇数，以保证在计算结果最后会产生一个较多的类别，如果取偶数可能会产生相等的情况，不利于预测。

K的取法

 　  常用的方法是从k=1开始，使用检验集估计分类器的误差率。重复该过程，每次K增值1，允许增加一个近邻。选取产生最小误差率的K。

　　一般k的取值不超过20，上限是n的开方，随着数据集的增大，K的值也要增大。

二、K-means

1.算法步骤

　　1)从n个数据中随机选择 k 个对象作为初始聚类中心；
　　2) 根据每个聚类对象的均值（中心对象），计算每个数据点与这些中心对象的距离；并根据最小距离准则，重新对数据进行划分；
　　3) 重新计算每个有变化的聚类簇的均值，选择与均值距离最小的数据作为中心对象；
　　4) 循环步骤2和3，直到每个聚类簇不再发生变化为止。

2.基本要素

• k值的选择：也就是类别的确定，k值的选择常用手肘法和轮廓系数法。
• 距离度量：可以采用欧氏距离、曼哈顿距离等。

 

3.手肘法

核心公式：SSE(sum of the squared errors，误差平方和)

$SSE=sum^K_{k=1}sum_{xin C_i}|x-m_i|^2$　

• $C_i$是第i个簇
• x是$C_i$中的样本点
• $m_i$是$C_i$的质心（$C_i$中所有样本的均值）
• SSE是所有样本的聚类误差，代表了聚类效果的好坏。

随着聚类数k的增大，样本划分会更加精细，每个簇的聚合程度会逐渐提高，那么误差平方和SSE自然会逐渐变小。当k小于真实聚类数时，由于k的增大会大幅增加每个簇的聚合程度，故SSE的下降幅度会很大，而当k到达真实聚类数时，再增加k所得到的聚合程度回报会迅速变小，所以SSE的下降幅度会骤减，然后随着k值的继续增大而趋于平缓，也就是说SSE和k的关系图是一个手肘的形状，而这个肘部对应的k值就是数据的真实聚类数。

 

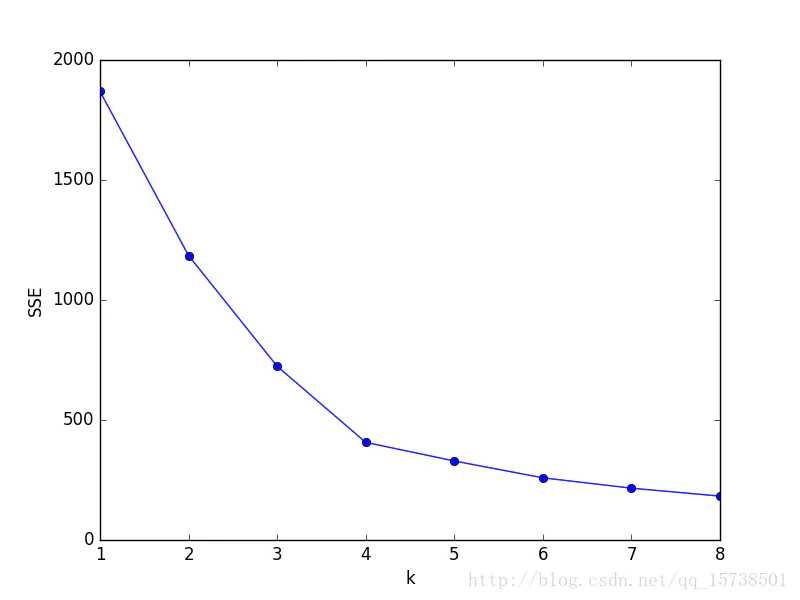
 显然，肘部对于的k值为4(曲率最高)，故对于这个数据集的聚类而言，最佳聚类数应该选4。

4.轮廓系数法

使用轮廓系数(silhouette coefficient)来确定，选择使系数较大所对应的k值
方法：

• 计算样本i到同簇其他样本的平均距离$a_i$。$a_i$越小，说明样本i越应该被聚类到该簇。将$a_i$ 称为样本i的簇内不相似度。
  簇C中所有样本的$a_i$均值称为簇C的簇不相似度。
• 计算样本i到其他某簇$C_j$的所有样本的平均距离$b_i^j$，称为样本i与簇$C_j$的不相似度。定义为样本i的簇间不相似度：$b_i =min{b_i^1, b_i^2, ..., b_i^k}$
  $b_i$越大，说明样本i越不属于其他簇。

• 根据样本i的簇内不相似度$a_i$和簇间不相似度$b_i$，定义样本i的轮廓系数

  
  
   

  

   
• 判断：
  轮廓系数范围在[-1,1]之间。该值越大，越合理。si接近1，则说明样本i聚类合理；si接近-1，则说明样本i更应该分类到另外的簇；若si 近似为0，则说明样本i在两个簇的边界上。
• 所有样本的$s_i$的均值称为聚类结果的轮廓系数，是该聚类是否合理、有效的度量。
• 使用轮廓系数(silhouette coefficient)来确定，选择使系数较大所对应的k值

 

参考链接：

https://www.cnblogs.com/jyroy/p/9427977.html

https://www.cnblogs.com/PiPifamily/p/8520405.html

https://www.jianshu.com/p/335b376174d4